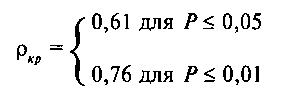Уровень статистической значимости



При обосновании статистического вывода следует решить вопрос, где же проходит линия между принятием и отвержением нулевой гипотезы? В силу наличия в эксперименте случайных влияний эта граница не может быть проведена абсолютно точно. Она базируется на понятии уровня значимости.Уровнемзначимостиназывается вероятность ошибочного отклонения нулевой гипотезы. Или, иными словами, уровеньзначимости—это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности, как правило, употребляют либо греческую букву α, либо латинскую букву р. В дальнейшем мы будем употреблять букву р.
Исторически сложилось так, что в прикладных науках, использующих статистику, и в частности в психологии, считается, что низшим уровнем статистической значимости является уровень р = 0,05; достаточным — уровень р = 0,01 и высшим уровень р = 0,001. Поэтому в статистических таблицах, которые приводятся в приложении к учебникам по статистике, обычно даются табличные значения для уровней р = 0,05, р = 0,01 и р = 0,001. Иногда даются табличные значения для уровней р — 0,025 и р = 0,005.
Величины 0,05, 0,01 и 0,001 — это так называемые стандартные уровни статистической значимости. При статистическом анализе экспериментальных данных психолог в зависимости от задач и гипотез исследования должен выбрать необходимый уровень значимости. Как видим, здесь наибольшая величина, или нижняя граница уровня статистической значимости, равняется 0,05 — это означает, что допускается пять ошибок в выборке из ста элементов (случаев, испытуемых) или одна ошибка из двадцати элементов (случаев, испытуемых). Считается, что ни шесть, ни семь, ни большее количество раз из ста мы ошибиться не можем. Цена таких ошибок будет слишком велика.
Заметим, что в современных статистических пакетах на ЭВМ используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначаемые буквой р, могут иметь различное числовое выражение в интервале от 0 до 1, например, р = 0,7, р = 0,23 или р = 0,012. Понятно, что в первых двух случаях полученные уровни значимости слишком велики и говорить о том, что результат значим нельзя. В то же время в последнем случае результаты значимы на уровне 12 тысячных. Это достоверный уровень.
Правило принятия статистического вывода таково: на основании полученных экспериментальных данных психолог подсчитывает по выбранному им статистическому методу так называемую эмпирическую статистику, или эмпирическое значение. Эту величину удобно обозначить как Чэмп. Затем эмпирическая статистика Чэмп сравнивается с двумя критическими величинами, которые соответствуют уровням значимости в 5% и в 1% для выбранного статистического метода и которые обозначаются как Чкр. Величины Чкр находятся для данного статистического метода по соответствующим таблицам, приведенным в приложении к любому учебнику по статистике. Эти величины, как правило, всегда различны и их в дальнейшем для удобства можно назвать как Чкр1 и Чкр2. Найденные по таблицам величины критических значений Чкр1 и Чкр2 удобно представлять в следующей стандартной форме записи:
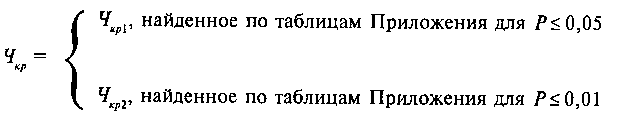 |
Подчеркнем, однако, что мы использовали обозначения Чэмп и Чкр как сокращение слова «число». Во всех статистических методах приняты свои символические обозначения всех этих величин: как подсчитанной по соответствующему статистическому методу эмпирической величины, так и найденных по соответствующим таблицам критических величин. Например, при подсчете рангового коэффициента корреляции Спирмена по таблице критических значений этого коэффициента были найдены следующие величины критических значений, которые для этого метода обозначаются греческой буквой ρ («ро»). Так для р = 0,05 по таблице найдена величина ρкр1 = 0,61 и для р = 0,01 величина ρкр2 = 0,76.
В принятой в дальнейшем изложении стандартной форме записи это выглядит следующим образом:
Теперь нам необходимо сравнить наше эмпирическое значение с двумя найденными по таблицам критическими значениями. Лучше всего это сделать, расположив все три числа на так называемой «оси значимости». «Ось значимости» представляет собой прямую, на левом конце которой располагается 0, хотя он, как правило, не отмечается на самой этой прямой, и слева направо идет увеличение числового ряда. По сути дела это привычная школьная ось абсцисс ОХ декартовой системы координат. Однако особенность этой оси в том, что на ней выделено три участка, «зоны». Одна крайняя зона называется зоной незначимости, вторая крайняя зона — зоной значимости, а промежуточная — зоной неопределенности. Границами всех трех зон являются Чкр1 для р = 0,05 и Чкр2 для р = 0,01, как это показано на рисунке.

В зависимости от правила принятия решения (правила вывода), предписанного в данном статистическом методе возможно два варианта.
Первый вариант: альтернативная гипотеза принимается, если Чэмп ≥ Чкр.
| Зона неопределенности |
| Зона незначимости |
| Зона значимости |
| 0,05 |
| 0,01 |
| Чкр1 |
| Чкр2 |
Или второй вариант: альтернативная гипотеза принимается, если Чэмп ≤ Чкр.
| Зона неопределенности |
| Зона значимости |
| Зона незначимости |
| 0,05 |
| 0,01 |
| Чкр1 |
| Чкр2 |
Подсчитанное Чэмп по какому либо статистическому методу должно обязательно попасть в одну из трех зон.
Если эмпирическое значение попадает в зону незначимости, то принимается гипотеза Н0 об отсутствии различий.
Если Чэмп попало в зону значимости, принимается альтернативная гипотеза Н1оналичии различий, а гипотеза Н0 отклоняется.
Если Чэмп попадает в зону неопределенности, перед исследователем стоит дилемма. Так, в зависимости от важности решаемой задачи он может считать полученную статистическую оценку достоверной на уровне 5%, и принять, тем самым гипотезу Н1, отклонив гипотезу Н0, либо — недостоверной на уровне 1%, приняв тем самым, гипотезу Н0. Подчеркнем, однако, что это именно тот случай, когда психолог может допустить ошибки первого или второго рода. Как уже говорилось выше, в этих обстоятельствах лучше всего увеличить объем выборки.
Подчеркнем также, что величина Чэмп может точно совпасть либо с Чкр1 либо Чкр2. В первом случае можно считать, что оценка достоверна точно на уровне в 5% и принять гипотезу Н1, или, напротив, принять гипотезу Н0. Во втором случае, как правило, принимается альтернативная гипотеза Н1 о наличии различий, а гипотеза Н0 отклоняется.
Источник
2.1.6 Уровни статистической значимости
Правило отклонения H 0 и принятия H 1
Если эмпирическое значение критерия равняется критическому значению, соответствующему р H 0 отклоняется, но мы еще не можем определенно принять H 1 . Если эмпирическое значение критерия равняется критическому значению, соответствующему р H 0 отклоняется и принимается H 1 .
Исключения: критерий знаков G , критерий-Т Вилкоксона и критерий- U Манна-Уитни. Для них устанавливаются обратные соотношения.
Для облегчения процесса принятия решения можно всякий раз вычерчивать «ось значимости».
Критические значения критерия обозначены как Q 0,05 и Q 0,01 , эмпирическое значение критерия как Q эмп . Оно заключено в эллипс.
Вправо от критического значения Q 0,01 простирается «зона значимости» — сюда попадают эмпирические значения, превышающие Q 0,01 и, следовательно, безусловно значимые.
Влево от критического значения Q 0,05 простирается «зона незначимости» , — сюда попадают эмпирические значения Q , которые ниже Q 0,05 , и, следовательно, безусловно незначимы.
Эмпирическое значение критерия попадает в область между Q 0,05 и Q 0,01 — Это зона «неопределенности» : мы уже можем отклонить гипотезу о недостоверности различий ( H 0 ), но еще не можем принять гипотезы об их достоверности ( H 1 ).
Практически, однако, исследователь может считать достоверными уже те различия, которые не попадают в зону незначимости, заявив, что они достоверны при р 2 , Фридмана, L — Пейджа, φ* Фишера, А, Колмогорова.
Уровень статистической значимости или критические значения критериев определяются поразному при проверке направленных и ненаправленных статистических гипотез.
При направленной статистической гипотезе используется односторонний критерий, при ненаправленной гипотезе — двусторонний критерий . Двусторонний критерий более строг, поскольку он проверяет различия в обе стороны, и поэтому то эмпирическое значение критерия, которое ранее соответствовало уровню значимости р
В данном руководстве исследователю не придется всякий раз самостоятельно решать, использует ли он односторонний или двухсторонний критерий. Таблицы критических значений критериев подобраны таким образом, что направленным гипотезам соответствует односторонний, а ненаправленным — двусторонний критерий, и приведенные значения удовлетворяют тем требованиям, которые предъявляются к каждому из них. Исследователю необходимо лишь следить за тем, чтобы его гипотезы совпадали по смыслу и по форме с гипотезами, предлагаемыми в описании каждого из критериев.
Источник
Понятие уровня статистической значимости



Первоначально всегда выдвигается гипотеза Н0. В процессе применения конкретного статистического метода перед психологом стоит дилемма: принять гипотезу Н0 или отклонить её и принять альтернативную гипотезу Н1. Очевидно, что возможны 4 варианта, которые можно оформить в виде таблицы.
| Решение | Верна Н0 | Верна Н1 |
| Н1 отклоняется | Ошибка 1рода | Правильное решение |
| Н0 не отклоняется | Правильное решение | Ошибка2 рода |
Понятно, что исследователя всегда интересует вопрос, насколько будет правильным его решение отклонить гипотезу Н0. Иными словами, какова вероятность ошибочного отклонения гипотезы Н0.
Уровень значимости – это вероятность ошибочного отклонения нулевой гипотезы, иными словами вероятность ошибки 1 рода.
Исторически сложилось так, что в прикладных науках, использующих статистику и в частности в психологии считается, что низшим уровнем значимости является уровень
Р = 0,05 ; достаточным уровнем значимости Р = 0,01 и высшим уровнем значимости Р = 0,001
(или Р = 5%; Р = 1%; Р = 0,1%).
Вероятность Р = 0,05 означает, 5 ошибок на 100 случаев или 1 ошибка на 20 случаев.
Вероятность Р = 0,01 означает 1 ошибку на 100 случаев.
Мы будем пользоваться уровнем значимости Р = 0,05 и Р = 0,01

Зона не значимости зона значимости
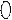
Ось значимости начинается с нуля, который обычно не отмечается. Полученные в результате применения конкретного метода эмпирические значения располагаются на оси значимости.
Критические значения находятся из специальных таблиц.
Эмпирические значения отмечают на оси без учёта знака. 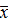
Если эмпирическое значение попадает в зону незначимости, то применяется Н0.
Если эмпирическое значение попадает в зону значимости, то Н0 отклоняется и принимается Н1.
Если эмпирическое значение попадает в зону неопределённости, то принимается Н0, но на уровне 5% значимости она может быть отклонена и принята гипотеза Н1.
Если эмпирическое значение совпадает с критическим, то попадает в следующую зону.
Источник