- Заряд релятивистски инвариантен что значит
- Заряд релятивистски инвариантен что значит
- Закон Кулона
- Электрическое поле
- Потенциал
- Связь между напряженностью электрического поля и потенциалом
- Лекция 1
- 1. Общие понятия
- 2. Способы получения наэлектризованных тел
- 3. Измерение заряда
- 4. Единица заряда
- 5. Закон сохранения заряда
- 6. Заряд Земли
- 7. Инвариантность заряда
- 8. Дискретность заряда
- 9. Модели заряженных тел
- 10. Точечный заряд
- 11. Дельта функция или функция Дирака.
Заряд релятивистски инвариантен что значит
Два вида электрического заряда. В современном представлении электрический заряд является таким же фундаментальным свойством микрочастицы, как, например, спин или её масса, а его существование в двух видах, называемых положительным и отрицательным зарядами, является проявлением фундаментальной симметрии, подобно правому и левому в пространстве или четности и нечетности в микромире.
Квантование электрического заряда. На основании большого числа экспериментов установлено, что электрический заряд квантуется, т. е. заряд любого тела кратен целому числу элементарных зарядов, каждый из которых имеет величину, равную 1,60 × 10 — 1 9 Кл. Этот элементарный заряд принято обозначать буквой e. Частицей с отрицательным элементарным зарядом является электрон ( me = 9,11 × 10 — 3 1 кг). Примером устойчивой частицы с положительным элементарным зарядом служит протон ( m р = 1,67 × 10 — 2 7 кг). Известна также частица с массой, равной массе электрона, и зарядом, равным заряду протона, получившая название позитрон.
Макроскопические тела, как правило, электрически нейтральны, т. е. в них в равных количествах содержатся как положительные, так и отрицательные заряды. Зарядить тело можно, создав в нем избыток заряженных частиц одного вида, например, трением о другое тело, в котором при этом образуется избыток зарядов противоположного вида. Учитывая наличие элементарного заряда, полный электрический заряд любого тела можно представить как q = ± N e , где N — целое число.
Сохранение электрического заряда. В 1747 г. американский физик Б. Франклин установил один из фундаментальных законов природы — закон сохранения электрического заряда, физической основой которого является точное равенство величин положительного и отрицательного элементарных зарядов. Этот закон формулируется так: « Алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе». Электрически изолированной принято считать систему, через поверхность которой нет переноса зарядов.
Релятивистская инвариантность электрического заряда. Фундаментальным свойством электрического заряда является его релятивистская инвариантность. Это свойство тесно связано с сохранением электрического заряда и означает в широком смысле, что в любой инерциальной системе отсчета полный электрический заряд сохраняется. Или в более узком смысле, что находящиеся в различных инерциальных системах наблюдатели, измеряя электрический заряд, получают одно и то же его значение. Таким образом, электрический заряд тела не зависит от того, движется тело или покоится.
1) В чем заключается закон сохранения заряда. Приведите примеры проявления этого закона
2) Некоторый заряд имеет в системе отсчета К величину q . Какова будет величина этого заряда q * в системе отсчета К * , движущейся относительно К со скоростью V
3) Какую систему можно считать электрически изолированной
4) Металлический шарик имеет 5,0 10 5 избыточных электронов. Каков его заряд в кулонах? Сколько избыточных электронов останется на шарике после соприкосновения с другим таким же шариком, заряд которого 3,2 10 -14 Кл.
(Ответ: — 8,0 10 -14 Кл; 1,5 10 5 электронов)
Источник
Заряд релятивистски инвариантен что значит
- заряды одного вида отталкиваются друг от друга, заряды разных видов — притягиваются, причем сила отталкивания равна по модулю силе притягивания;
- число положительных и отрицательных зарядов во Вселенной одинаковое.
- минимальный заряд частицы e = 1.60·10 -19 Кл;
- любой заряд q кратен минимальному, т.е. q=Ne, где N — целое число;
- минимальные положительный и отрицательный заряды равны по абсолютной величине.
Закон Кулона
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой.
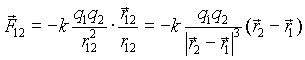 (1.1)
(1.1) 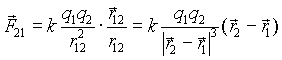
Здесь k — множитель, зависящий от выбранной системы единиц. В системе СИ его принято записывать как 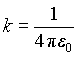
Закон Кулона установлен экспериментально, но его справедливость подтверждается и тем, что с опытом согласуются все выводы теории, в основе которой лежит этот закон.
Как показывает опыт, сила взаимодействия двух зарядов не изменяется при наличии третьего заряда. Поэтому, независимо от числа зарядов выражения (1.1)-(1.2) можно использовать для вычисления силы взаимодействия каждой пары. Тогда при наличии многих зарядов сила, действующая на заряд 1 со стороны всех остальных зарядов есть
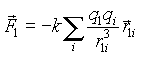
Электрическое поле
Заряд изменяет свойства окружающего его пространства, т.е. он создает вокруг себя нечто материальное, посредством чего осуществляется взаимодействие между зарядами. Это нечто и называется электрическим полем. Для обнаружения и исследования электрического поля нужно воспользоваться пробным зарядом. Пробный заряд должен быть точечным и малым (чтобы не искажать поле своим присутствием). Поле характеризуется величиной напряженности, которая численно равна силе, действующей на единичный пробный заряд:
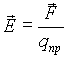
Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд.
В математике вводится определение векторного поля как части пространства, каждой точке которого сопоставлен вектор. Так совокупность векторов E образует поле вектора напряженности электрического поля. Графически поле E изображается при помощи силовых линий напряженности.
Из (1.3)-(1.4) следует, что напряженность поля системы зарядов равна векторной сумме напряженности полей, которые создавал бы каждый из зарядов системы в отдельности:
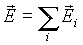
Это положение называется принципом суперпозиции. Следует отметить, что выражение (1.5) отнюдь не тривиально, а выражает собой закон природы.
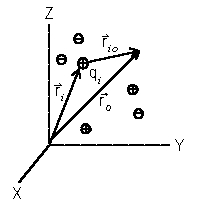
Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Пусть имеется N точечных зарядов разных знаков, расположенных в точках пространства, с радиус-векторами ri . Требуется найти поле в точке с радиус-вектором ro . Тогда, так как rio = ro—ri , то результирующее поле будет равно:
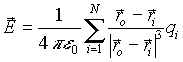
Заряды qi подставляются в (1.6) со своими знаками.
Если заряды не точечные, то их разбивают на малые доли dq, которые могут считаться точечными и тогда
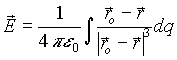
где интегрирование производится по всей области распределения заряда.
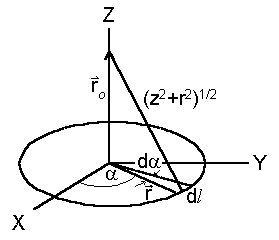
Разобъем кольцо на бесконечно малые участки dl, на каждый из которых приходится заряд dq, равный:
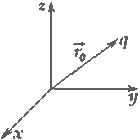
Введем систему координат, как показано на рис. 1.3. Радиусы векторы точки наблюдения и элемента dl равны, соответственно:
В силу симметрии распределения заряда проекции Ex и Ey вектора E в любой точке на оси кольца должны быть равны нулю. Тогда E= Ez k. Проекцию Ez найдем по формуле (1.7):
Равенство нулю проекций Ex и Ey можно получить и чисто формально из (1.7):
Потенциал
Поскольку электростатическое поле является центральным, то оно консервативно. Работа по перемещению пробного заряда q‘ из точки 1 в точку 2 не зависит от пути и выражается, как
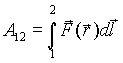
Для центральной силы 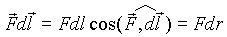
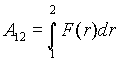
Для кулоновской силы, действующей на пробный заряд q‘ со стороны точечного заряда q, имеем
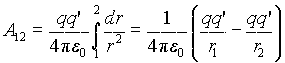
Работа сил консервативного поля может быть представлена как убыль потенциальной энергии Wp при переходе от точки 1 к точке 2:
Тогда потенциальная энергия заряда q‘ в поле заряда q есть
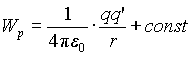
Выбирая константу так, чтобы Wp = 0 при 
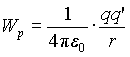
Величина 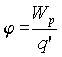
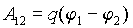
Тогда, так как потенциал на бесконечности положен равным нулю то можно сказать, что потенциал равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Единицей потенциала является Вольт. 1В — это потенциал в такой точке, для перемещения в которую из бесконечности заряда в 1Кл нужно затратить работу в 1Дж.
В силу принципа суперпозиции потенциал поля, создаваемого системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:
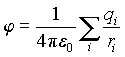
Если заряд распределен непрерывно с объемной плотностью ρ(r), то, переходя в (1.15) от суммирования к интегрированию по бесконечно малым зарядам ρdV, получим
Связь между напряженностью электрического поля и потенциалом
Как известно, в потенциальном поле сила может быть получена из потенциальной энергии из соотношения
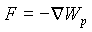
Тогда для напряженности электрического поля из соотношений
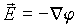
С другой стороны, из соотношений (1.8) и (1.14) следует, что
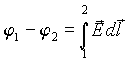
Поверхности равного потенциала, т.е. такие поверхности, на которых 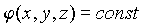
Источник
Лекция 1
1. Общие понятия
 | Электрический заряд – это физическая величина, определяющая электромагнитное поле, посредством которого осуществляется взаимодействие между зарядами. Несмотря на различные способы получения заряда, существует электричество только двух сортов: «стеклянное» и «смоляное» («+» и «–»). Хотя существует мнение, что на самом деле это избыток или недостаток электричества одного сорта, а именно отрицательного. В природе количество положительного электричества примерно равно количеству отрицательного. 2. Способы получения наэлектризованных телИз любого источника тока | |
 |  |  |
3. Измерение заряда
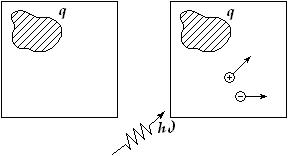
 | Пробный заряд – это заряд, который не вносит искажений в существующее поле. Пусть существует некоторое электрическое поле. В какую-то точку поля помещаем пробный заряд. Поле на него будет действовать с некоторой силой. Вносим в это поле другой пробный заряд. Если силы направлены в одну сторону, то заряды одноименные, если нет, то разноименные. Зная отношения сил, знаем и отношение зарядов, а, приняв один из зарядов за эталон, указываем принципиальный способ измерения зарядов. 4. Единица заряда
|
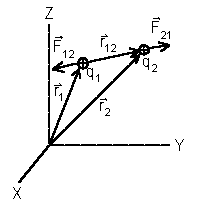
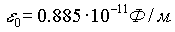
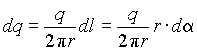
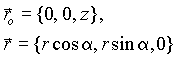
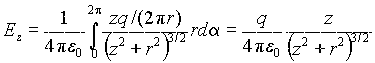
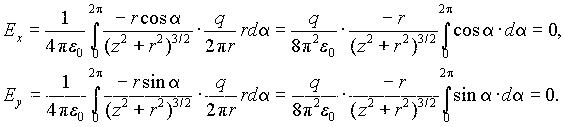
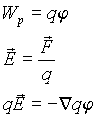
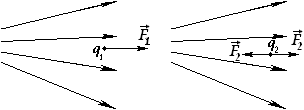
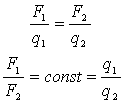
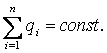
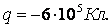
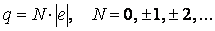
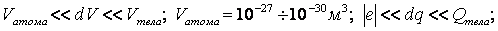
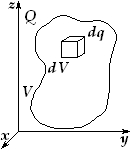
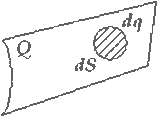
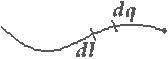
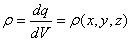
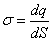
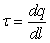
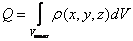
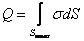
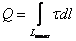
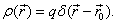
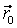 – радиус-вектор, определяющий положение точечного заряда;
– радиус-вектор, определяющий положение точечного заряда; 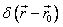 – дельта-функция Дирака.
– дельта-функция Дирака.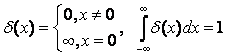
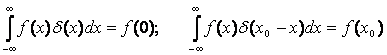
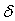 — функция:
— функция: