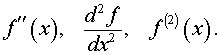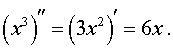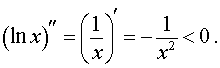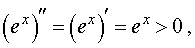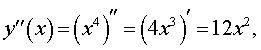Вторая производная равна нулю что это значит

Вторая производная равна нулю что это значит

7. Геометрический смысл второй производной

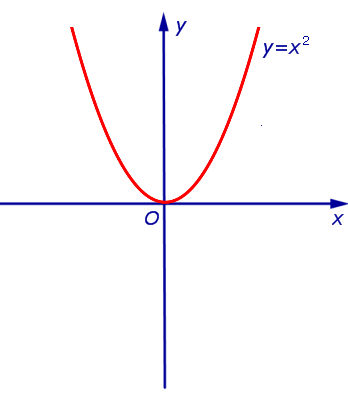
Вторая производная f» (x) имеет также важное значение в анализе и в геометрии; в самом деле, представляя собой скорость изменения наклона f (х) кривой y = f (x), вторая производная дает указание на то, как изогнута кривая. Если в некотором промежутке вторая производная больше нуля, то скорость изменения наклона f’ (х) положительна. Положительный знак скорости изменения некоторой функции указывает на то, что эта функция возрастает с возрастанием аргумента х. Следовательно, неравенство f» (х) > 0 указывает на то, что наклон f (x) есть возрастающая функция х и, значит, при увеличении х кривая становится более крутой там, где наклон ее положителен, и более пологой там, где наклон отрицателен. Условимся говорить, что в этом случае кривая вогнута (рис. 270). Аналогично если f» (х) 2 всюду вогнута, так как ее вторая производная (f» (х) = 2) всегда положительна. Кривая y = f (х) = x 3 вогнута при х>0 и выпукла при х 2 = 0 (но нет ни минимума, ни максимума!), а также и f» (х) = 0 при х = 0. Эта точка называется тезкой перегиба. В точках, которые так называются, касательная (в данном случае ось х) пересекает кривую.

Если буква s обозначает длину дуги кривой, а буква α — угол наклона, то функция α = h (s) есть функция переменного s. При передвижении точки по кривой функция α = h (s) будет меняться. Скорость этого изменения h’ (s) принято называть кривизной кривой в точке, для которой длина дуги равна s. Без доказательства отметим, что кривизна k может быть выражена с помощью первой и второй производных от функции y = f (x), определяющей кривую, согласно следующей формуле:

Источник

Исследование функции на выпуклость вверх и выпуклость вниз
с помощью второй производной

Выпуклые вверх функции

Выпуклые вниз функции

Вторая производная функции

Достаточные условия выпуклости вверх и выпуклости вниз функции

Точки перегиба

Необходимые условия для существования точки перегиба

Достаточные условия для существования точки перегиба

Выпуклые вверх функции

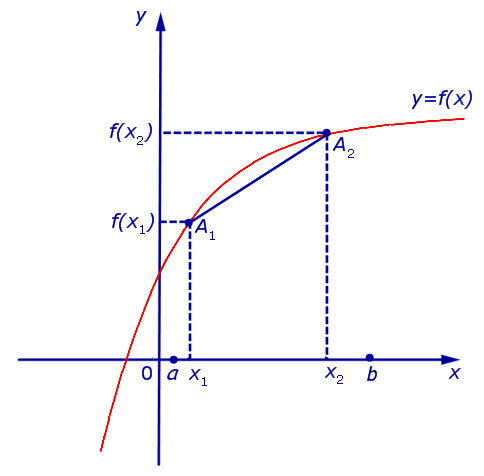
Определение 1. Функцию y = f (x) называют выпуклой вверх на интервале (a, b) , если для любых двух точек 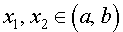таких, что x₁ график функции y = f (x) расположен выше отрезка, соединяющего точки A₁ = (x₁; f (x₁)) и A₂ = (x₂; f (x₂)) .

Функция, график которой изображен на рисунке 1, выпукла вверх на интервале (a, b) .

Пример 1. Примером функции, выпуклой вверх на 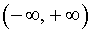, является функция y = – x 2 (рис. 2).

Выпуклые вниз функции

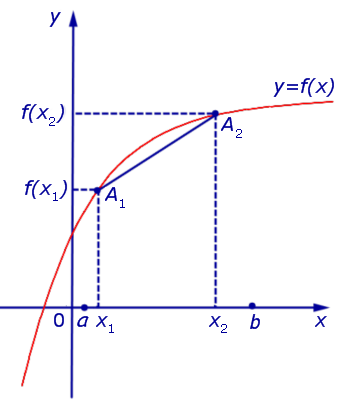
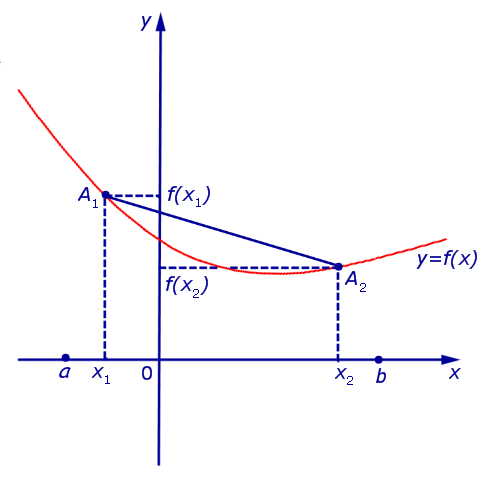
Определение 2. Функцию y = f (x) называют выпуклой вниз на интервале (a, b) , если для любых двух точек 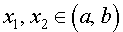таких, что x₁ график функции y = f (x) расположен ниже отрезка, соединяющего точки A₁ = (x₁; f (x₁)) и A₂ = (x₂; f (x₂)) .

Функция, график которой изображен на рисунке 3, выпукла вниз на интервале (a, b) .

Пример 2. Примером функции, выпуклой вниз на 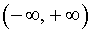, является функция y = x 2 (рис. 4).

Вторая производная функции

Определение 3. Если у функции y = f (x) существует производная в некоторой точке x₀ , то эту производную часто называют первой производной или производной первого порядка функции y = f (x) в точке x₀ .

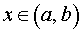
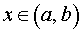
Пусть у функции y = f (x) существует производная во всех точках . Тогда, вычисляя в каждой точке производную f ‘ (x) , мы получим функцию y = f ‘ (x). Если у функции y = f ‘ (x) существует производная в некоторой точке x₀ интервала (a, b), то эту производную называют второй производной или производной второго порядка функции y = f (x) в точке x₀ .

Для производной второго порядка y = f (x) используются обозначения:

Точно так же, как это было сделано при определении второй производной функции f (x), можно определить и производные более высоких порядков: третью производную, четвертую производную и т.д. (конечно же, при условии, что они существуют).

Достаточные условия выпуклости вверх и выпуклости вниз функции

При исследовании направления выпуклости функции (выпуклость вверх или выпуклость вниз) важную роль играет вторая производная этой функции.

Утверждение 1. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 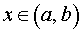выполнено условие

то функция f (x) выпукла вниз на интервале (a, b) .

Утверждение 2. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 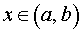выполнено условие

Доказательства утверждений 1 и 2 выходят за рамки школьного курса математики и здесь не приводятся.

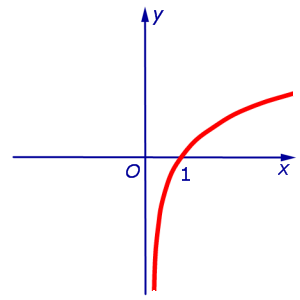
Пример 3. Функция y = ln x на интервале 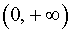удовлетворяет условию

В силу утверждения 2 отсюда следует, что функция y = ln x выпукла вверх (рис. 5) на всей своей области определения .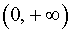

Пример 4. Функция y = e x на интервале 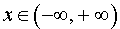удовлетворяет условию

и, в силу утверждения 1, функция y = e x выпукла вниз (рис. 6) на всей своей области определения .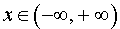

Точки перегиба

Определение 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x₀ . Говорят, что при переходе через точку x₀ функция f (x) меняет направление выпуклости, если на одном из интервалов

Определение 5. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x₀ , а у графика функции в точке (x₀; f (x₀)) существует касательная. Если функция f (x) при переходе через точку x₀ меняет направление выпуклости, то точку x₀ называют точкой перегиба функции f (x) .

Замечание 1 . Если x₀ – точка перегиба функции y = f (x), то график функции y = f (x) при переходе через точку x₀ переходит с одной стороны от касательной в точке (x₀; f (x₀)) на другую сторону от касательной, то есть «перегибается» через касательную.

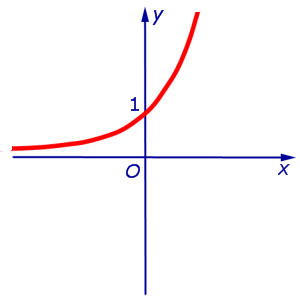
Пример 5. Рассмотрим функцию y = x 3 , график которой изображен на рисунке 7.

то прямая y = 0 (ось абсцисс Ox ) является касательной к графику функции y = x 3 в точке (0; 0).

Поэтому y» > 0 при x > 0 и y» при x Таким образом, функция y = x 3 выпукла вверх при x и выпукла вниз при x > 0 , и точка x = 0 является точкой перегиба графика функции y = x 3 . График функции y = x 3 при переходе через точку x = 0 переходит из нижней полуплоскости в верхнюю полуплоскость, то есть «перегибается» через касательную y = 0 .

Необходимые условия для существования точки перегиба

Замечание 2. Условия существования точки перегиба, сформулированные в утверждении 3, являются необходимыми, но не являются достаточными.

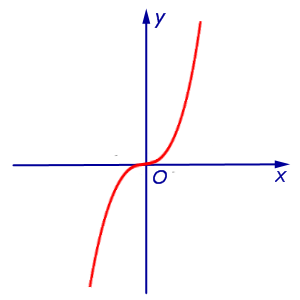
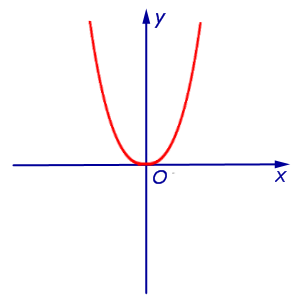
Действительно, рассмотрим функцию y = x 4 , график которой изображен на рисунке 8.

Вычисляя вторую производную этой функции

замечаем, что y » (0) = 0 , однако точка x = 0 не является точкой перегиба графика функции y = x 4 , так как функция y = x 4 выпукла вниз, как при x так и при x > 0 .

Достаточные условия для существования точки перегиба

Утверждение 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x₀ , имеет первую производную в каждой точке интервала (a, b) и имеет вторую производную в каждой точке интервала (a, b) за исключением, быть может, самой точки x₀ .

Если для точек 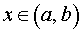выполнено условие:

либо выполнено условие:

Другими словами, точка x₀ является точкой перегиба графика функции f (x) , если при переходе через точку x₀ вторая производная функции меняет свой знак.

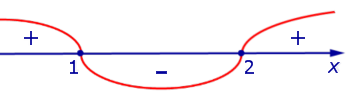
Пример 6. Найти интервалы, на которых функция

выпукла вверх, а также интервалы, на которых эта функция выпукла вниз. Определить точки перегиба.

Решение. Вычислим вторую производную функции:

Отсюда вытекает, что вторая производная существует во всех точках 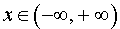и обращается в нуль в точках x = 1 и x = 2 . Воспользуемся методом интервалов и изобразим на рисунке 9 диаграмму знаков второй производной y» (x)

При переходе через точку x = 1 вторая производная функции y» (x) меняет знак с «+» на «–» . Следовательно, x = 1 – точка перегиба графика функции.

При переходе через точку x = 2 вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, x = 2 также является точкой перегиба графика функции.

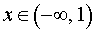
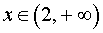
При и при 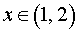вторая производная функции y» (x) > 0, следовательно, функция y (x) выпукла вниз на этих интервалах.

При вторая производная функции y» (x) следовательно, функция y (x) выпукла вверх на интервале (1, 2) .

Источник

Узнать ещё

Знание — сила. Познавательная информация

График второй производной

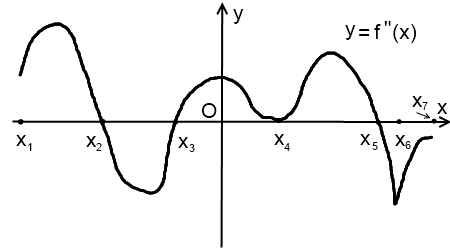
Рассмотрим, что можно сказать о функции, анализируя график ее второй производной.

Что мы знаем связи второй производной

с исходной функцией y=f(x)?

1) Функция y=f(x) выпукла вниз на промежутках, где вторая производная положительна

0.\]» title=»Rendered by QuickLaTeX.com»/>

2) Функция y=f(x) выпукла вверх на промежутках, где вторая производная отрицательна

3) Функция y=f(x) имеет критические точки второго рода в точках, в которых вторая производная равна нулю или не существует (речь идет только о внутренних точках области определения фу н кции. Точки на концах области определения не рассматриваем).

4) Функция y=f(x) имеет точки перегиба в точках, в которых вторая производная меняет знак.

5) С учетом того, что x0 — точка максимума функции f(x), если

точки максимума, если они есть, на графике второй производной лежат ниже оси OX.

Соответственно, x* — точка минимума функции f(x), если

0,\]» title=»Rendered by QuickLaTeX.com»/>

поэтому точки минимума, если они есть, на графике второй производной лежат выше оси OX.

На промежутках (x1; x2) и (x3;x5) вторая производная неотрицательна (в точке x4 она равна нулю, но смены знака нет). Значит, на этих промежутках функция y=f(x) выпукла вниз.

На промежутках (x2; x3) и (x5; x7) вторая производная отрицательна. Поэтому на этих промежутках функция y=f(x) выпукла вверх.

В точках x2, x3, x4, x5 вторая производная равна нулю, в точке x6 — не существует. Это — критические точки второго рода.

Производная меняет знак в точках x2, x3, x5. Следовательно, это — точки перегиба.

Источник