Укажи порядок числа что это значит

Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.

Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.

Любое рациональное число может быть представлено в виде:

Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок.

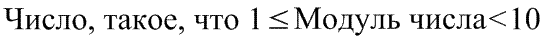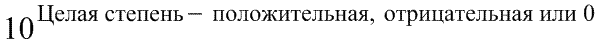Эта часть записи называется Мантиссой числа в стандартной (научной) форме.	А эта часть называется Порядком числа в стандартной (научной) форме.

Пример 1: Число 7984 в стандартной форме записывается как 7,984*10 3 , где 7,984 — мантисса а 10 3 — порядок.

Пример 2 : Величины 890 и 45932, записанные в стандартной форме выглядят как: 8,9*10 2 и 4,5932*10 4 и отличаются на 2 порядка = имеют разницу в 2 порядка. Числа 7,5 и 75 различаются на порядок ( на 1 порядок) = имеют разницу в 1 порядок, что бы там в телевизоре не думали. И так далее.

Очевидно, что при сложении и вычитании чисел записанных в стандартной форме и имеющих один порядок, достаточно сложить или вычесть мантиссы.

Пример 3: 7,2*10 34 + 1,2*10 34 = (7,2+ 1,2)*10 34 =8,4*10 34

Единственный способ корректно сложить или вычесть числа разных порядков — это выразить одно из них в нестандартной форме:

Пример 4: 9,9*10 13 + 9,9*10 12 =9,9*10 13 + 0,99*10 13 = (9,9+ 0,99)*10 13 =10,89*10 13 =1,089*10 14

Очень удобно проводить операции умножения и деления с числами, записанными в стандартной форме, пользуясь правилами действий со степенями:

Пример 5: 4,0*10 3 x 2,25*10 2 =(4,0×2,25)x(10 3+2 )= 9,0*10 5

Пример 6: 5,0*10 6 /2,5*10 3 =(5,0/2,5)x(10 6-3 )= 2,0*10 3

И теперь, если уж Вы дочитали до этого места, самое главное — зачем это придумано: попробуйте сравнить на глаз числа 970984567234109879 и 1211121111211121112125? Впечатляет? А попробуйте их же в стандартном виде: 9,70984567234109879*10 17 и 1,211121111211121112125*10 21 . Понятно, что первое на 4 порядка меньше? Понятно, что величина первого по отношению ко второму ниже, чем точность большинства расчетных моделей? Понятно, что в большинстве практических случаев первую величину вообще не следует брать в расчет, если вклад величин в процесс пропорционален? Понятно, что изменение второй величины на 10% значительно превосходит изменение первой в 3 раза? и т.д. Просто, оказывается, инженеры их жены и дети так устроены, что с этими числами очень удобно работать.

Источник

Cтандартный вид числа

В задачах по физике часто приходится работать с очень большими и очень малыми величинами.

Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?

Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.

Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число « 10 » в различных степенях.

• 10 − 2 =
  

  1

  10 2

  =

  1

  100

  = 0,01 (более подробно об отрицательной степени можно прочитать в уроке 9 класса «Отрицательная степень»)

• 10 −1 =
  

  1

  10 1

  =

  1

  10

  = 0,1

• 10 0 = 1
• 10 1 = 10
• 10 2 = 100
• 10 3 = 1000
• …

Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..

• 5 · 10 = 50
• 27 · 100 = 2 700
• 18 · 1000 = 18 000

Теперь запишем тоже самое, используя определение степени.

• 5 · 10 = 5 · 10 1 = 50
• 27 · 100 = 27 · 10 2 = 2 700
• 18 · 1000 = 18 · 10 3 = 18 000

При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.

• 13 000 : 100 =
  

  13 000

  100

  = 130

• 50 : 10 =
  

  50

  10

  = 5

Для десятичных дробей действует схожее правило умножения на 10, 100, 1000 . При умножении десятичной дроби на 10, 100, 1000 и т.д. мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д.

• 5,7 · 100 = 570
• 7,013 · 10 = 70,13
• 68,3 · 1000 = 68 300

С помощью степени можно записать вычисления выше следующим образом:

• 5,7 · 100 = 5,7 · 10 2 = 570
• 7,013 · 10 = 7,013 · 10 1 = 70,13
• 68,3 · 1000 = 68,3 · 10 3 = 68 300

При делении на 10, 100, 1000 и т.д. перемещаем запятую влево .

• 6,7 : 10 =
  

  6,7

  10

  = 0,67

• 0,15 : 100 =
  

  0,15

  100

  = 0,0015

С помощью определения отрицательной степени можно записать вычисления выше следующим образом:

• 6,7 : 10 =
  

  6,7

  10

  = 6,7 · 10 −1 = 0,67

• 0,15 : 100 =
  

  0,15

  100

  = 0,15 · 10 −2 = 0,0015

Стандартный вид числа

Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.

Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:

Такая запись называется — стандартный вид числа.
При этом число « n » называют порядком числа « a ».

Из определения выше важно понять, что степень, в которой стоит « 10 », в стандартном виде числа называется порядком .

Теперь к примеру. Пусть нам дано число « 5 600 » и требуется записать его в стандартном виде.

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».

В числе « 5 600 » первая цифра справа — « 5 ». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.

Значит, чтобы из « 5 , 600 » получить « 5600 » нам нужно умножить « 5 , 600 » на « 1000 ». Запишем полученное преобразование.

Теперь запишем « 1000 » с использованием степени.

Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.

Таким образом « 5 600 » в стандартном виде будет выглядеть следующим образом:

Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.

Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь « 0,017 ».

Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от « 1 » до « 9 ».

В десятичной дроби « 0,017 » вначале идет « 0 ». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от « 0 ».

Это цифра « 1 ». Посчитаем сколько знаков (цифр) стояло от запятой до цифры « 1 », включая саму цифру « 1 ».

Получается два знака. Начнем записывать « 0,017 » в стандартном виде. Перенесем запятую и поставим ее справа от « 1 ».

Ответим себе на вопрос: «На что нужно умножить или разделить « 1,7 », чтобы получить изначальное число « 0,017 » ?». Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится влево .

Выходит, чтобы из « 1,7 » сделать 0,017 », нужно « 1,7 разделить на « 100 » (чтобы перенести запятую на два знака влево).

Запишем это деление на « 100 », используя обыкновенную дробь.

С помощью отрицательной степени запишем окончательный вид числа « 0,017 » в стандартном виде.

0,017 = 1,7 : 100 = 1,7 ·

1

100

=
1,7 · 10 −2

Примеры решения задач
на запись числа в стандартном виде

№ 237 Алимов 8 класс

(Устно) Определить порядок числа, выражающего значение физической константы:

1) масса покоя электрона
m_e = 9,1093897 · 10 −31

Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень, в которой стоит « 10 ». В данном примере « 10 » стоит в
степени « −31 ». Значит, порядком массы покоя электрона является « −31 ».

№ 238 Алимов 8 класс

Записать в стандартном виде и определить порядок числа k , выражающего физического константу:

2) постоянная Фарадея
F = 96485,309 Кл/моль;

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».

Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра « 9 ».

Зададим себе вопрос: «На что нужно умножить « 9 , 6485309 », чтобы получить « 96485 , 309 » ?» Посчитаем количество знаков (цифр), на которое требуется перенести запятую в « 96485 , 309 », чтобы получить « 96485309 ».

Получается « 4 » знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:

Порядком числа « 9,6485309 · 10 4 » является степень, в которой стоит « 10 ». Следовательно, порядок « k = 4 ».

Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:

Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую, чтобы из « 2 , 686763 » получить « 2686763 ».

Значит, чтобы получить из « 2 , 686763 » нужно изначальное число « 2686763 » умножить на « 10 6 ».

Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».

Источник

Урок алгебры в 8-м классе по теме «Стандартный вид числа» с использованием регионального компонента

Разделы: Математика

Создание условий, которые способствуют знакомству обучающихся с основными данными по Кемеровской области. Что в свою очередь воспитывает чувство гордости за родной край, воспитывает чувство патриотизма.

Овладение обучающимися понятием стандартного вида числа и развитие навыков решения задач с числами, записанными в стандартном виде.

1. Познакомить обучающихся с определением стандартного вида числа и объяснить, почему необходимо записывать числа в стандартном виде.
2. Научить представлять любое число в стандартном виде.
3. Закрепить полученные знания в ходе выполнения упражнений.

Сторона любимая, приметная,
У тебя есть приметы предметные.
Только вот им верить не приходится-
Все они изменчивы, как водится.
Где-то есть такие ж кедры с соснами,
Где-то есть такие ж зимы с вёснами,
Горы есть со снеговыми шапками
И посёлки с трубами и шахтами.
Только нет нигде чего-то главного.
По цене одной лишь жизни равного,
Очень близкого чего-то очень местного,
Сердцу только одному известного.
Стоит лишь откуда-то вернуться,
Как готово сердце захлебнуться,
Весь мой век такое с ним случается.
Пробовал унять – не получается.

Виктор Баянов, известный кузбасский поэт.

МЕТОДЫ: объяснительно — иллюстративный

ХОД УРОКА

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

УЧИТЕЛЬ: Здравствуйте, ребята! Вы, наверное, обратили внимание, что на доске записано стихотворение. Это необычно? Конечно! Но и урок у нас сегодня немного необычный. Мы будем изучать новый материал по алгебре, используя данные о нашем родном крае – Кемеровской области, где мы живём и учимся. (Учитель читает стихотворение кузбасского поэта В. Баянова, являющиеся эпиграфом данного урока.)

Но прежде, чем переходить к новой теме, предлагаю вам провести гимнастику для ума – поработать устно: вспомнить изученные правила, посчитать и подготовиться к знакомству с новой темой.

2. УСТНАЯ РАБОТА.

а) 2 6 * 2 -4 ; б) 3 -2 *72; в) -3 + ( 1/3) -3 ; г) (0,01) -1 – 165.

2). Упростите: а) 0,5х -3 *у 3 * 4х 5 * у -1 ;

б) 12х 6 у -2 : (3х 2 у -5 ).

3). Вычислите: а) 3,2 * 10; б) 0,032 * 100;

в) 0,032*1000; г) 32,3 : 10; д) 32,3 : 100; е) 32,3 : 1000.

3. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.

УЧИТЕЛЬ: В науке и технике встречаются как очень большие, так и очень маленькие числа. Например, большим числом выражается объём Земли, а малым – диаметр молекулы воды. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними действия. В таком случае оказывается полезным представление числа в виде а * 10 п , где

п – целое число, а число а больше либо равно 1, но меньше10.Например, площадь Кемеровской области 95500 км 2 ; 95500 = 9,5 * 10 4 .Размеры молекулы приблизительно 0,0000003см,

0,0000003 = 3*10 -7 . Представление числа в таком виде называется представлением числа в стандартном виде. Число п называется порядком числа а. Порядок числа даёт представление о том, насколько велико или мало рассматриваемое число. Так, если порядок числа равен 3, то это означает, что число больше либо равно1000, но меньше 10000. Если же порядок равен -2, то число больше либо равно 0,01, но меньше 0,1. Большой положительный порядок показывает, что число очень велико, а большой по модулю отрицательный порядок показывает, что число очень мало. Предлагаю сегодня на уроке использовать данные только по Кемеровской области. Это наш край и мы должны изучать его во всем его многообразии и знать. Это наша малая Родина, наша вторая мать!

Рассмотрим некоторые примеры (учитель записывает подробно на доске, объясняет запись, прибегает к помощи обучающихся. Обучающиеся записывают в тетрадях, внимательно слушают, задают вопросы по ходу решения и отвечают на вопросы педагога).

25 000 = 2,5 * 10 4 ; 1230 = 1,23 * 10 3 ; 0,0036 = 3,6 * 10 -3 ; 24 = 2,4 * 10; 0,5 = 5 * 10 -1 ; 0,00038 = 3,8 * 10 — 4 ; 560 000 000 = 5,6 * 10 8 ; 967 000 000 000 000 = 9,67 * 10 14 ; 0, 000 000 000 000 000 028 = 2,8 * 10 – 17 .

4. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО В ХОДЕ ВЫПОЛНЕНИЯ УПРАЖНЕНИЙ.

(Учитель готовит плакаты формата А4 с записанными на них данными по Кемеровской области. С помощью магнитов плакаты поочередно вывешиваются на доску. После записи очередного числа плакат убирается и заменяется следующим. Картинки с изображением животных и птиц вывешиваются на доску вместе с числом. Учитель комментирует плакаты, появляющиеся на доске. Картинки с изображением птиц и животных можно позаимствовать у учителя биологии или скачать из интернета, привлечь к работе можно учащихся 8 класса по желанию. Из опыта работы хочу сказать, что желающих бывает много, но необходимо помнить и об исполнительской дисциплине каждого ученика. Выполнение задания лучше проверить заранее, чтобы избежать срыва урока).

ПРИМЕР 1. Представьте в стандартном виде следующие величины:

• Самые древние горные породы, слагающие земную кору нашей области имеют возраст 1 700 000 000 лет (1,7 * 10 9 )
• Кузнецкий каменноугольный бассейн — самый крупный в мире с запасами 631 000 000 000 тонн (6,31 * 10 11 )
• Длина границ нашей области 2 520 000 м (2,5 * 10 6 ).Из них по горным районам – 1 210 000 м (1,2 * 10 6 ), по равнинам и возвышенностям – 980 000 м (9,8 *10 5 ), по водным рубежам – 330 000 м (3,3 * 10 5 ).
• Самая высокая точка родного края расположена в Кузнецком Алатау – Верхний Зуб (Арзамас — Таскыл) – 2178 м (2,178 *10 3 ), а самая низкая – при впадении реки Большая Чёрная в Томь – 78 м (7,8 * 10). Таким образом перепады высот нашей области составляют 2100 м (2,1 *10 2 ).
• Ласка – самый маленький и отважный хищник. Длина её тела от 13 до 26 см. (1,3 *10 и 2,6 *10)
• Самый запасливый из обладателей защёчных мешков – бурундук. В своих кладовых он запасает до 8000 г орехов. (8 *10 3 )
• Зимой за день бурундук съедает 0,004 кг запасов (4 * 10 -3 ).
• Самым долгоживущим и очень редким в нашей области является журавль. Он доживает до 82 лет (8,2 *10)

ПРИМЕР 2. Прочтите числа, записанные в стандартном виде:

• Самое большое кладбище динозавров на территории СНГ – это правый берег реки Кии у села Шестаково Чебулинского района имеет возраст 1,3*10 8 лет.
• Самый большой по весу метеорит упал на территорию области в районе верховий реки Малая Кондома и весил он 1,23 * 10 2 кг.
• Самая большая водная артерия Кузбасса – река Томь – имеет протяженность 8,27 * 10 5 м.
• Самой остроглазой из ночных хищников является сова. Она видит неподвижную мышь при освещении всего 2 * 10 -6 люкса. Но даже если станет в 4,6 * 10 4 раз светлее, все другие птицы мышь не заметят.
• Самая маленькая птица наших лесов – королёк. За год она поедает до 10 7 вредных насекомых.
• Самые распространенные промысловые птицы нашей области – это рябчики ( их 1,2 * 10 5 ), тетерева (2,6 *10 4 ) и глухари (2*10 4 )

ЗАДАНИЕ: Представьте указанные данные в стандартном виде. Отметьте в таблице ответы и буквы, им соответствующие. Оставшиеся буквы зачеркните и прочтите название самой крупной из осёдлых птиц Кемеровской области, которая весит до 5 кг.

1. Зона лесов Кемеровской области занимает 60 165 000 м 2 .
2. На западных склонах Кузнецкого Алатау выпадает до 2500 мм осадков.
3. Самое большое озеро края Большой Берчикуль с площадью водного зеркала 32 000 м 2 .
4. Река Чулым имеет длину 1 799 000 м.
5. Самые воинствующие из насекомых Кузбасса – рыжие муравьи. За день обитатели только одного муравейника уничтожают до 100 000 насекомых.
6. Самый маленький хищник на Земле — ласка. Длина её тела хвоста до 0,05 м. Но этот крохотный зверёк отважен до невероятности. Она душит даже зайца, который намного крупнее её.
7. Самое интересное насекомое – пчела. Для сбора 1кг мёда одной пчеле нужно посетить 19 000 000 цветов.

Источник