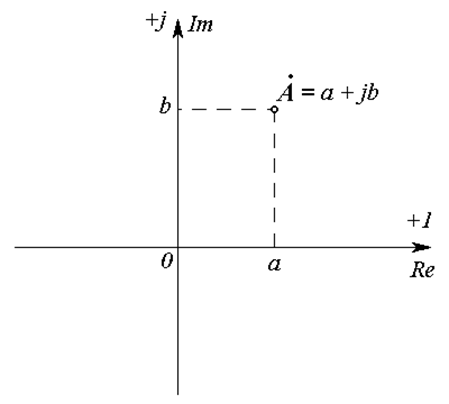Основы электротехники и электроники: Курс лекций , страница 13
Символический метод позволяет перейти от графоаналитических расчетов с помощью векторных диаграмм к расчетам аналитическим. Это, с одной стороны, повышает точность расчетов, а с другой – значительно облегчает выполнение математических операций с синусоидальными функциями. Кроме того, символический метод позволяет без ограничений использовать для расчета цепей синусоидального тока все законы и методы, полученные для цепей постоянного тока.
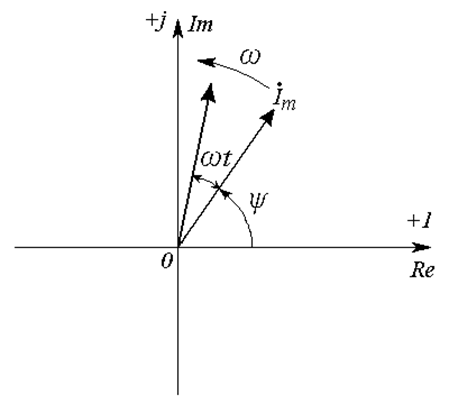
Основная идея метода состоит в перенесении известной нам векторной диаграммы на комплексную плоскость. Пусть на комплексной плоскости со скоростью 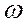
Сразу заметим, что в теоретической электротехнике принято обозначать мнимую единицу (то есть квадратный корень из минус единицы) буквой j (читается по-немецки, «йот»), чтобы не путать ее с обозначением тока.
Также все комплексные величины, изображающие токи, напряжения и мощности, принято обозначать прописной буквой с точкой сверху. Комплексные величины, изображающие параметры цепи (сопротивления, проводимости), принято обозначать прописной буквой, подчеркнутой снизу. Модуль комплексного числа будем обозначать прописной буквой, без точки и черты.
Если функция тока имеет вид:
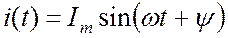
то изображающая ее комплексная функция:
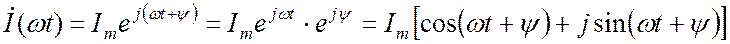
Очевидно, что исходная синусоидальная функция (18.1) совпадает с мнимой частью комплексной функции (18.2).
Как правило, в цепях действуют источники одной и той же частоты, поэтому нет необходимости вращать векторы. А это означает, что сомножитель 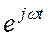
Итак, все реальные синусоидальные функции заменяются комплексными числами. Расчеты проводятся в комплексной форме. Окончательный результат переводится в синусоидальную форму.
Заметим, что чаще всего при расчетах используются не амплитудные, а действующие значения токов и напряжений. Следует придерживаться этого правила.
Рассмотрим некоторые свойства комплексных чисел.
Как известно, любое комплексное число можно изобразить точкой на комплексной плоскости. В зависимости от способа описания координат этой точки можно выделить две формы комплексного числа – алгебраическую и показательную.
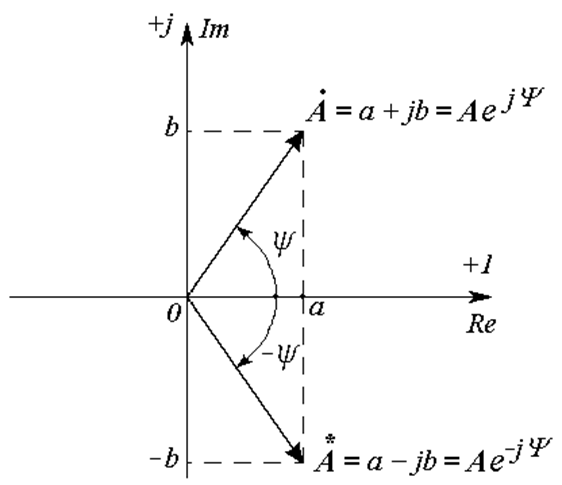
Алгебраическая форма комплексного числа соответствует декартовой системе координат на комплексной плоскости (Рис. 18.2):
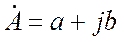
где a – действительная часть числа (координата по оси Re);
b – мнимая часть числа (координата по оси Im).
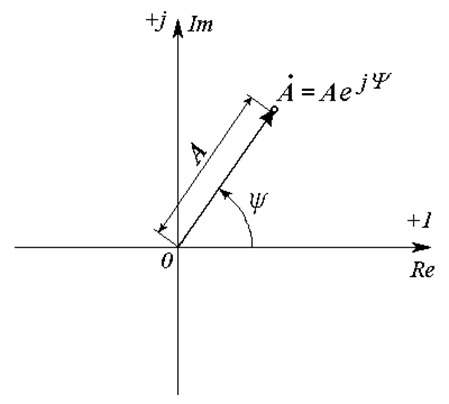
Показательная форма комплексного числа соответствует полярной системе координат на комплексной плоскости (Рис. 18.3):
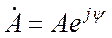
где A – модуль комплексного числа (длина радиус-вектора, соединяющего начало координат
с точкой 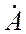
Ψ – угол комплексного числа (откладывается от положительной полуоси действительных
чисел; против часовой стрелки – со знаком плюс, по часовой стрелке – со знаком минус).
Алгебраическая и показательная формы связаны друг с другом через тригонометрическую форму комплексного числа:
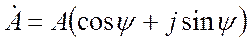
Из (18.5) выводятся формулы для перевода комплексного числа из одной формы в другую.
При переводе комплексного числа из показательной формы в алгебраическую используют соотношения:
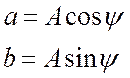
При переводе комплексного числа из алгебраической формы в показательную используют соотношения:
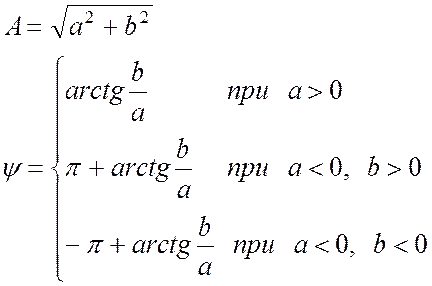
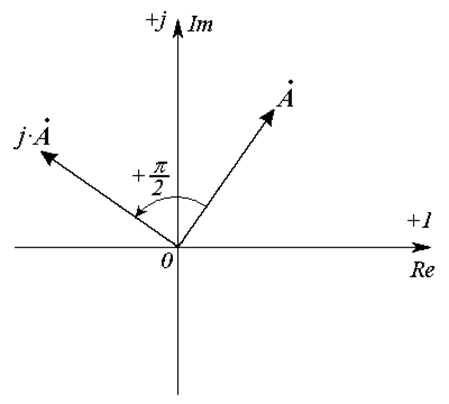
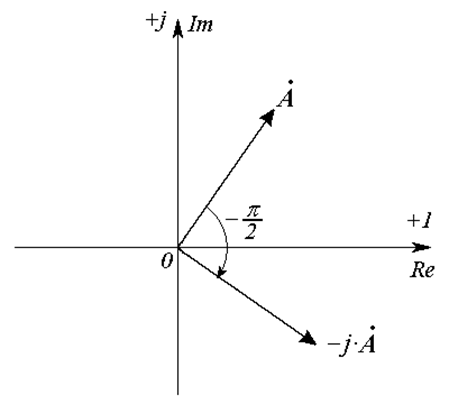
Умножение комплексного числа на 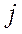
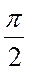
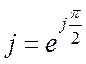
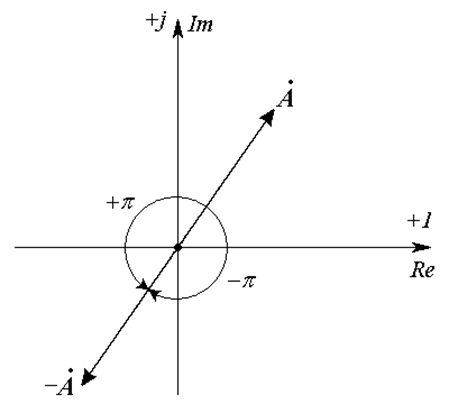
Умножение комплексного числа на 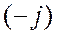
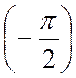
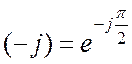
Умножение комплексного числа на 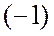
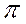
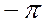
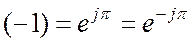
Дифференцирование синусоидальной функции соответствует умножению ее комплексного изображения на 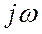
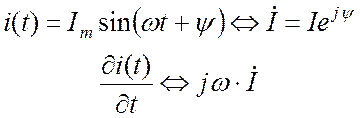
Интегрирование синусоидальной функции соответствует делению ее комплексного изображения на 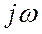
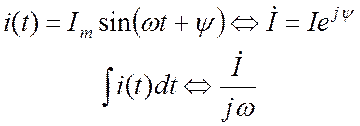
Если в знаменателе дроби стоит чисто мнимое число (то есть число, действительная часть которого равна нулю), мнимая единица переносится в числитель путем умножения числителя и знаменателя на 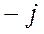
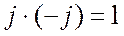
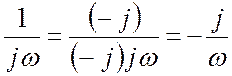
Если в знаменателе дроби стоит число с неравной нулю действительной частью, числитель и знаменатель дроби умножают на комплексно-сопряженное число. Комплексно-сопряженным числом называют число, симметричное данному относительно действительной оси (Рис. 18.7). Обозначается звездочкой сверху.
Здесь используется известное равенство:
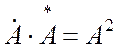
Произведение двух комплексно-сопряженных чисел равно квадрату их модуля.
Для переноса мнимой единицы в числитель умножим числитель и знаменатель на комплексно-сопряженное число:
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
Источник
Электрический ток, напряжение — простым языком!
Всем привет, на связи с вами снова Лёха Герыч.
Так вот я как-то размышлял о аудитории читающей мой блог: «Кто он? Кто тот посетитель моего блога, что каждый день заходит почитать мои посты?». Может быть это прошаренный спец зашел из любопытства почитать что я тут накалякал? А может это какой -нибудь доктор радиотехнических наук зашел посмотреть как спаять схему мультивибратора? 🙂
Знаете все это маловероятно, потому как для прошаренного специалиста все это уже пройденный этап и скорее всего все уже не так интересно и они сами с усами. Им может быть интересно лишь из праздного любопытства, мне конечно очень приятно и я жду каждого с распростертыми объятьями. Так что я пришел к выводу, что основной контингент моего блога да и большинства радиолюбительских сайтов это новички и любители рыскающие по интернету в поисках полезной информации.
Я вспоминаю себя, когда я искал в интернете какую-нибудь простенькую схемку чтобы с чего-нибудь начать, но постоянно что-то не подходило, что-то казалось заумным. Мне не хватало азов, таких, чтобы можно было по принципу от простого к сложному начать разбираться в интересующей меня теме.
Что такое напряжение и ток?
Кстати действительно что же такое электрический ток и напряжение? Я думаю, что никто на самом деле и не знает, ведь чтобы это знать это надо хотя бы видеть. Кто может видеть ток, бегущий по проводам?
Да никто, человечество еще не достигло таких технологий, чтобы воочию наблюдать движения электрических зарядов. Все что мы видим в учебниках и научных трудах это некая абстракция созданная в результате многочисленных наблюдений.
Об этом можно много рассуждать… Давай те попробуем разобраться, что такое электрический ток и напряжение. Я не буду писать определения, определения не дают самого понимания сути. Если интересно, возьмите любой учебник по физике.
Мы не видим электрического тока и всех процессов протекающих в проводнике, тогда попробуем создать аналогию.
Традиционно электрический ток текущий в проводнике сравнивают с водой бегущей по трубам. В нашей аналогии вода это электрический ток. Вода бежит по трубам с определенной скоростью, скорость это сила тока, измеряемая в амперах. Ну трубы это само собой проводник.
Хорошо, электрический ток мы себе представили, но а что такое напряжение? Сейчас помозгуем.
Вода в трубе, в отсутствии каких-либо сил (сила тяжести, давления) теч не будет, она будет покоиться как и любая другая жижа вылитая на пол. Так вот эта сила или точнее сказать энергия в нашей водопроводной аналогии и будет тем самым напряжением.
Что происходит с водой бегущей из резервуара расположенного высоко над землей? Вода устремляется бурным потоком из резервуара к поверхности земли, гонимая силами тяготения. И чем выше от земли расположен резервуар тем с большей скоростью вытекает вода из шланга. Понимаете о чем я говорю?
Чем выше резервуар, тем больше сила (читай напряжение) воздействующая на воду. И тем больше скорость водного потока (читай сила тока). Теперь становится понятно и в голове начинает создаваться красочная картинка.
С понятием напряжения электрического тока тесно связано понятие «потенциал» , или «разность потенциалов». Хорошо, обратимся снова к нашей водопроводной аналогии.
Резервуар находится на возвышенности что позволяет воде беспрепятственно стекать по трубе вниз. Так как бак с водой на высоте, то и потенциал этой точки будет более высоким или более положительным чем тот что находится на уровне земли. Видите что получается?
У нас появилось две точки имеющие разные потенциалы, точнее разную величину потенциала.
Получается, для того чтобы электрический ток мог бежать по проводу, потенциалы не должны быть равны. Ток бежит от точки с большим потенциалом к точки с меньшим потенциалом.
Помните такое выражение, что ток бежит от плюса к минусу. Так вот это все тоже самое. Плюс это более положительный потенциал а минус более отрицательный.
Кстати а хотите вопрос на засыпку? Что произойдет с током, если величины потенциалов будет периодически меняться местами?
Тогда мы будем наблюдать то как электрический ток меняет свое направление на противоположное каждый раз как потенциалы поменяются. Это получится уже переменный ток. Но его мы пока рассматривать не будем, дабы в голове сформировалось ясное понимание процессов.
Измерение напряжения.
Для замера напряжение используется прибор вольтметр, хотя сейчас наиболее популярны мультиметры. Мультиметр это такой комбинированный прибор имеющий в себе много чего. )))
Вольтметр это как раз тот прибор который измеряет разность потенциалов между двумя точками. Напряжение (разность потенциалов) в любой точке схемы обычно измеряется относительно НОЛЯ или ЗЕМЛИ или МАССЫ или МИНУСА батарейки. Не важно главное это должна быть точка имеющая наименьший потенциал во всей схеме.
Итак чтобы измерить напряжение постоянного тока между двумя точками, делаем следующее. Черный (минусовой) щуп вольтметра втыкается в ту точку, где предположительно мы можем наблюдать точку с меньшим потенциалом (НОЛЬ). Красный щуп (плюсовой) втыкаем в точку, потенциал которой нам интересен.
И результатом измерения будет числовое значение разности потенциалов, или другими словами напряжение.
Измерение тока.
В отличие от напряжения, которое замеряется в двух точках, величина тока замеряется в одной точке. Так как сила тока (или говорят просто ток) по нашей аналогии есть скорость течения воды, то эту скорость нужно замерять только в одной точке.
Нам нужно распилить водопровод и вставить в разрыв некий счетчик, который будет подсчитывать литры и минуты.
Аналогично если вернемся в реальный мир нашей электрической модели, то получим тоже самое. Чтобы замерить величину электрического тока, нам нужно подключить в разрыв электрической цепи нехитрый прибор — амперметр. Амперметр также входит в состав мультиметра.
Щупы мультиметра нужно переставить в режим измерения тока. Затем перекусываем наш проводник, и подключаем обрывки провода к мультиметру и вуаля — на экране мультиметра будет показана величина тока.
Закон Ома.
Думаю что мы, не теряли время даром. Ознакомившись с нашими водопроводными моделями в голове начал складываться пазл, начало формироваться понимание.
Попробуем проверить его на законе Ома.
I — ток измеряемый в Амперах (А);
U — напряжение измеряемое в Вольтах (В);
R — cопротивление измеряемое в Омах (Ом)
Ом нам говорил, что Электрический ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Про сопротивление я сегодня не говорил, но я думаю что вы поняли. Сопротивление электрическому току оказывается материалом проводника. В нашей водопроводной системе сопротивление току воды оказывают ржавые трубы, забитые ржавчиной и прочей какой. 🙂
Таким образом закон Ома работает во всей своей красе что для водопроводной системы, что для электрической. Может быть мне податься в сантехники, уж очень много схожего. 🙂
Чем выше задран резервуар с водой, тем быстрее по трубам будет теч вода. Но если трубы загажены то скорость будет меньше. Чем больше сопротивление воде тем медленнее она будет теч. Если засор, то вода вообще может встать.
Ну и для электричества. Величина тока зависит прямо пропорционально от величины напряжения (разности потенциалов), и обратно пропорционально зависит от сопротивления.
Чем выше напряжение тем больше величина тока, но чем больше сопротивление тем меньше величина тока. Напряжение может быть очень большим, но ток может не теч из-за обрыва. А обрыв это все равно, что если вместо металлического проводника мы подключили проводник из воздуха, а воздух обладает просто гигантским сопротивлением. Вот ток и остановится.
Вот и подходит время закругляться, вроде все что хотел сказать в этой статье я сказал. Если остаются какие-либо вопросы спрашивайте в комментариях.
Источник