- Область допустимых значений функции
- Допустимые и недопустимые значения переменных
- Что такое ОДЗ
- Как найти ОДЗ: примеры решения
- Запомните
- Зачем учитывать ОДЗ при преобразовании выражения
- При каких значениях переменной x имеет смысл выражение
- Ответ или решение 1
- Для того, чтобы ответить на вопрос задачи составим план действий
- Найдем значения переменной x при которых выражение 10/√(x — 2) имеет смысл
- 1. Рациональные выражения
- Упражнения
Область допустимых значений функции
О чем эта статья:
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 0, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).
Читать запись нужно вот так:
Область допустимых значений переменной x для выражения 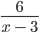
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
- требуется извлечение квадратного корня из отрицательного числа;
- присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 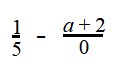
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Запомните
- Если число входит в ОДЗ, то около числа ставим квадратные скобки.
- Если число не входит в ОДЗ, то около него ставятся круглые скобки.
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
- расширить ОДЗ
- никак не повлиять на ОДЗ
- сузить ОДЗ
Рассмотрим каждый случай в отдельности.
Пример 7
Рассмотрим выражение a + 4/a — 4/a
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 8
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 9
Рассмотрим выражение
ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Источник
При каких значениях переменной x имеет смысл выражение
Ответ или решение 1
Нам нужно найти те значения переменной x при которых выражение 10/√(x — 2) имеет смысл.
Для того, чтобы ответить на вопрос задачи составим план действий
- первым действием мы должны рассмотреть и проанализировать заданное выражение;
- так как переменная находится в знаменателе дроби посмотрим какие условия на него налагаются, чтобы выражение имело смысл;
- составим линейное неравенство;
- решим полученное неравенство и запишем ответ к заданию.
Найдем значения переменной x при которых выражение 10/√(x — 2) имеет смысл
Давайте рассмотрим заданное выражение и проанализируем его.
Заданное выражение представлено в виде дроби. Числитель дроби равен 10, а знаменатель √(x — 2).
Знак дроби в математике равносилен знаку деления.
Переменная находится в знаменателе дроби, значит мы должны исключить из области допустимых значений значение переменной, которая обращает знаменатель в ноль.
Но помимо этого в знаменателе находится знак квадратного корня, а мы знаем, что корень из отрицательного числа не имеет смысла.
То есть на знаменатель дроби наложены следующие условия:
√(x — 2) ≠ 0; х — 2 ≥ 0.
То есть, чтобы найти ОДЗ выражения мы должны решить линейное неравенство.
Решаем полученное линейное неравенство по аналогии с линейным уравнением.
Переносим в правую часть неравенства -2, при переносе меняем знак слагаемого на плюс. При этом знак неравенства остается тем же.
Итак, при x принадлежащему промежутку (2; + бесконечности) выражение 10/√(x — 2) имеет смысл.
Ответ: x принадлежит промежутку (2; + бесконечности).
Источник
1. Рациональные выражения
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действии сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение 

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида 
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдём допустимые значения переменной в дроби
Решение Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а — 9) = 0. Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Пример 2. При каком значении х значение дроби 
Решение Дробь 
Числитель дроби 
Упражнения

являются целыми, какие — дробными?
Из рациональных выражений

выпишите те, которые являются:
а) целыми выражениями;
б) дробными выражениями.
 при у = 3; 1; -5;
при у = 3; 1; -5;  ; -1,6; 100.
; -1,6; 100.
Чему равно значение дроби 
- а) Из формулы
выразите: переменную s через v и t; переменную t через s и v.
б) Из формулывыразите переменную V через ρ и m.
- Из городов А и В, расстояние между которыми s км, вышли в одно и то же время навстречу друг другу два поезда. Первый шёл со скоростью v1 км/ч, а второй — со скоростью v2 км/ч. Через t ч они встретились. Выразите переменную t через s, v1 и v2. Найдите значение t, если известно, что:
а) s = 250, v1 = 60, v2 = 40;
б) s = 310, v1 = 75, v2 = 80.
Составьте дробь:
а) числитель которой — произведение переменных х и у, а знаменатель — их сумма;
б) числитель которой — разность переменных а и b, а знаменатель — их произведение;
в) числитель которой — сумма переменных с и d, а знаменатель — их разность.
При каких значениях переменной имеет смысл рациональное выражение:
Укажите допустимые значения переменной в выражении:
Найдите допустимые значения переменной в выражении:
Найдите область определения функции:
При каком значении переменной значение дроби 
а) 1; б) 0; в) -1; г) 3?
При каких значениях переменной равно нулю значение дроби:
Определите знак дроби 
Докажите, что при любом значении переменной значение дроби:
При каком значении а принимает наибольшее значение дробь:
При каком значении Ъ принимает наименьшее значение дробь:
Чему равно наибольшее значение дроби 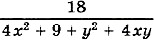
1. Равно 0; 2. Равно 1; 3. Равно 2; 4. Равно 3
Преобразуйте в многочлен:
Разложите на множители:
Источник

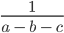
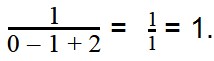
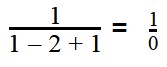
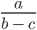
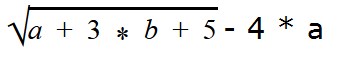
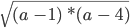
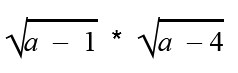








 выразите: переменную s через v и t; переменную t через s и v.
выразите: переменную s через v и t; переменную t через s и v.  выразите переменную V через ρ и m.
выразите переменную V через ρ и m.











