Ось вам что значит

так-ось

1 так-ось

2 так-от

См. также в других словарях:

так-ось — і так о/т, незм., част. Уживається в реченні для підтвердження стверджування чогось, вираження рішучості намірів та ін … Український тлумачний словник

так-от — див. так ось … Український тлумачний словник

ОСЬ ЛЕГКОГОНАМАГНИЧИВАНИЯ — направление в кристалле, в к ром ориентирован вектор намагниченности М магн … Физическая энциклопедия

Ось времени — Ось времени, временная ось (именуемая также в контексте термодинамики стрелою времени) концепция, описывающая время как прямую (то есть математически одномерный объект), протянутую из прошлого в будущее. Из любых двух несовпадающих точек… … Википедия

Ось конечности — Ось конечности представлет собой условную линию, вдоль которой распространяется основная механическая нагрузка на тело или его часть. Является важным понятием в ревматологии и травматалогии. На способность конечности выдерживать осевую… … Википедия

Ось (значения) — Ось (слово «ось» происходит от древнерусского «ость» долгий усик на плевеле каждого зерна колосовых растений или волос в пушном товаре) понятие некой центральной прямой, в том числе воображаемой прямой (линии): В технике:… … Википедия

Ось зла (значения) — Ось зла (политика) термин для обозначения перечня режимов (стран), спонсирующих, по мнению США, терроризм или разрабатывающих оружие массового поражения и способных передать его террористам. Ось зла (астрономия) протяжённая область («ось»… … Википедия

Ось зла — Ось зла: Ось зла (политика) термин для обозначения перечня режимов (стран), спонсирующих, по мнению США, терроризм или разрабатывающих оружие массового поражения и способных передать его террористам. Ось зла (астрономия) протяжённая… … Википедия

Ось мира (значения) — Ось мира (лат. Axis mundi) в мифологии и религии ось, связывающая небо и землю. Ось мира (астрономия) диаметр, вокруг которого происходит вращение небесной сферы (см. Небесная сфера). Ось Мира (англ. Axis for Peace) конференция,… … Википедия

Ось мира — Традиционные религии Ключевые понятия Бог · … Википедия

Ось Мира — Традиционные религии Типология Анимизм · Культ предков · Магия · Полидоксия · Спиритизм · Тенгрианство · … Википедия

Источник

Значение слова «ось»

1. Стержень, на котором укрепляют колесо, вращающиеся части машин, механизмов и т. п. Ось телеги.□ Коляска с отломленною заднею осью неуклюже лежала в грязи. Григорович, Проселочные дороги.

2. Спец. Прямая, проходящая через центр симметрии или центр тяжести какого-л. тела. Ось симметрии. Ось вращения. Ось кристалла. Ось резьбы. Ось самолета.

3. перен.; чего или какая. То основное, главное, вокруг которого развертываются какие-л. события, действия. Ось событий.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Ось (от праславян. ость) — серединная линия. В ботанике устаревшая форма — ость — продолжает использоваться.

в геометрии: ось — воображаемая прямая являющаяся визуальным, или натуральным центром вращающегося элемента;

в аналитических разделах математики: ось — линия базиса системы координат; например, ордината

в физике: ось вращения — основное понятие при изучении вращательного движения: также оно используется в географии, астрономии

в технике: ось — стержень, на концах которого помещаются колёса. Оси бывают вращающиеся и неподвижные (относительно колеса). В отличие от вала, ось не предназначена для передачи крутящего момента.

и другие примеры.

ОСЬ, и, мн. е́й, ж. 1. Деревянный или металлический стержень, на концах к-рого помещаются колеса. Тележная о. Вагонная о. Автомобильная о. Задняя о. 2. Прямая линия, проходящая внутри какого-н. тела и обладающая особыми свойствами (напр. неподвижностью при вращении тела, прохождением через геометрический центр симметрии и т. п.; мат., физ.). О. вращения. О. симметрии. Оптическая о. О. кристалла. 3. перен. Главнейшее основное направление, вокруг к-рого развертываются события, явления (книжн. ритор.). О. переговоров — достижение соглашения об ограничении вооружений.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

1. центральный стержень, на котором крепится колесо или иная вращающаяся деталь ◆ Своему брату я говорю: сила пара движет поршни, поршни приводят в движение ось, ось поворачивает колёса, а колёса, упирая в воду, движут вперёд корабль, называемый пароход. Лев Толстой, «О языке народных книжек», 1862 г. (цитата из Викитеки)

2. воображаемая прямая, рассматриваемая как центр вращения или симметрии чего-либо ◆ Ось тре́тьего поря́дка куби́ческих криста́ллов пири́та ориентирована перпендикулярно пове́рхности гра́ней ромбо́эдра кальци́та. А. А. Антонов, «Минералогия родингитов Баженовского гипербазитового массива», 2003 г. (цитата из НКРЯ) ◆ У большинства планет, включая Землю, ось вращения расположена почти вертикально, то есть перпендикулярно к плоскости орбиты планеты. Георгий Бурба, «Открытый дважды», 2004 г. // «Вокруг света» (цитата из НКРЯ)

3. перен. книжн. ритор. главное основное направление, вокруг которого разворачиваются какие-либо события, явления ◆ Ось переговоров — достижение соглашения об ограничении вооружений. ◆ Сде́лать э́то откры́то вряд ли полу́чится по внутриполити́ческим причи́нам ― как в США, так и в Китае, но э́то ещё не по́вод, что́бы не протяну́ть дипломати́ческую ось Вашингтон-Пекин че́рез Москву. Сергей Минаев, «Двадцатым будешь?», 2002 г. // «Вечерняя Москва» (цитата из НКРЯ)

Источник

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Прямоугольная система координат. Ось абсцисс и ординат

О чем эта статья:

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

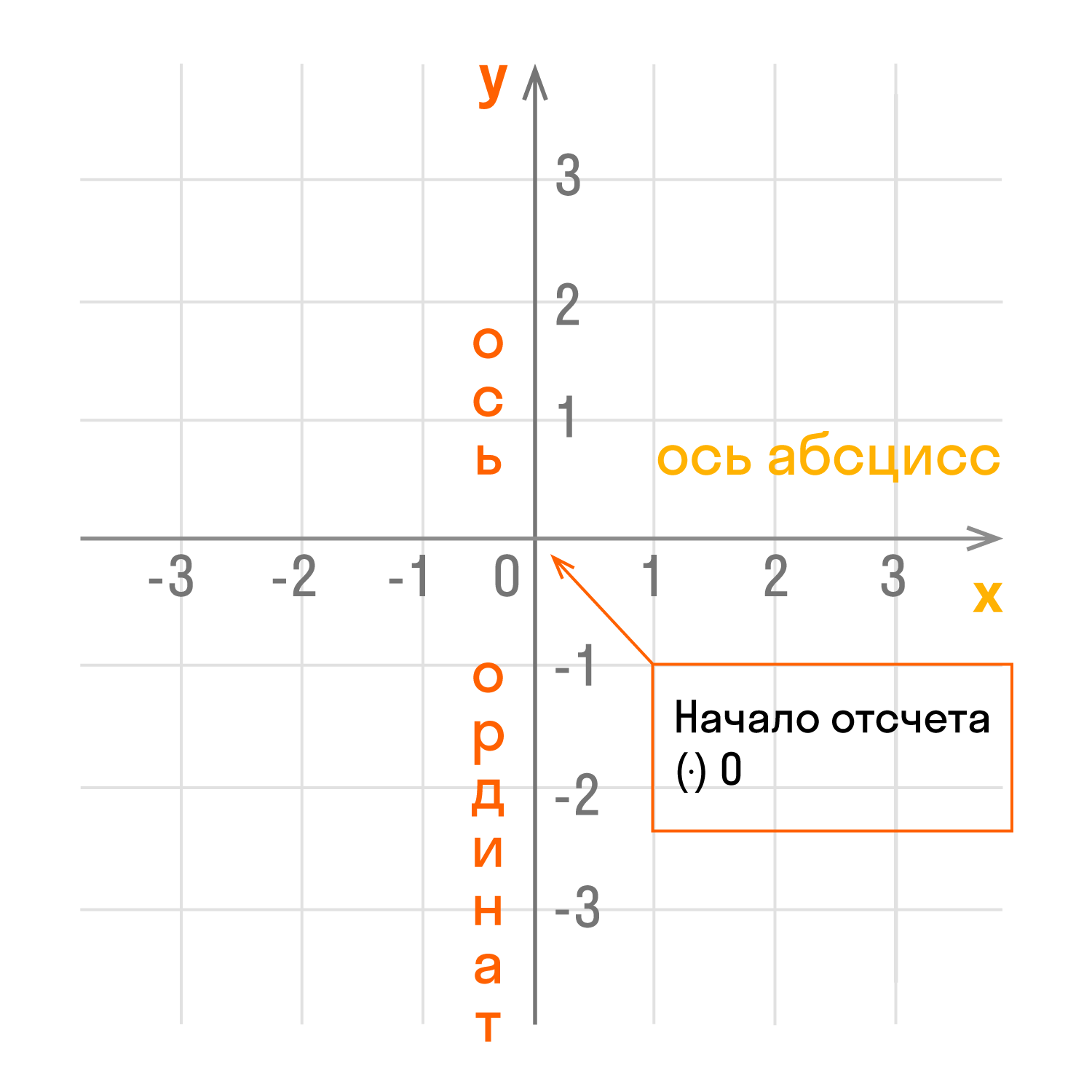
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

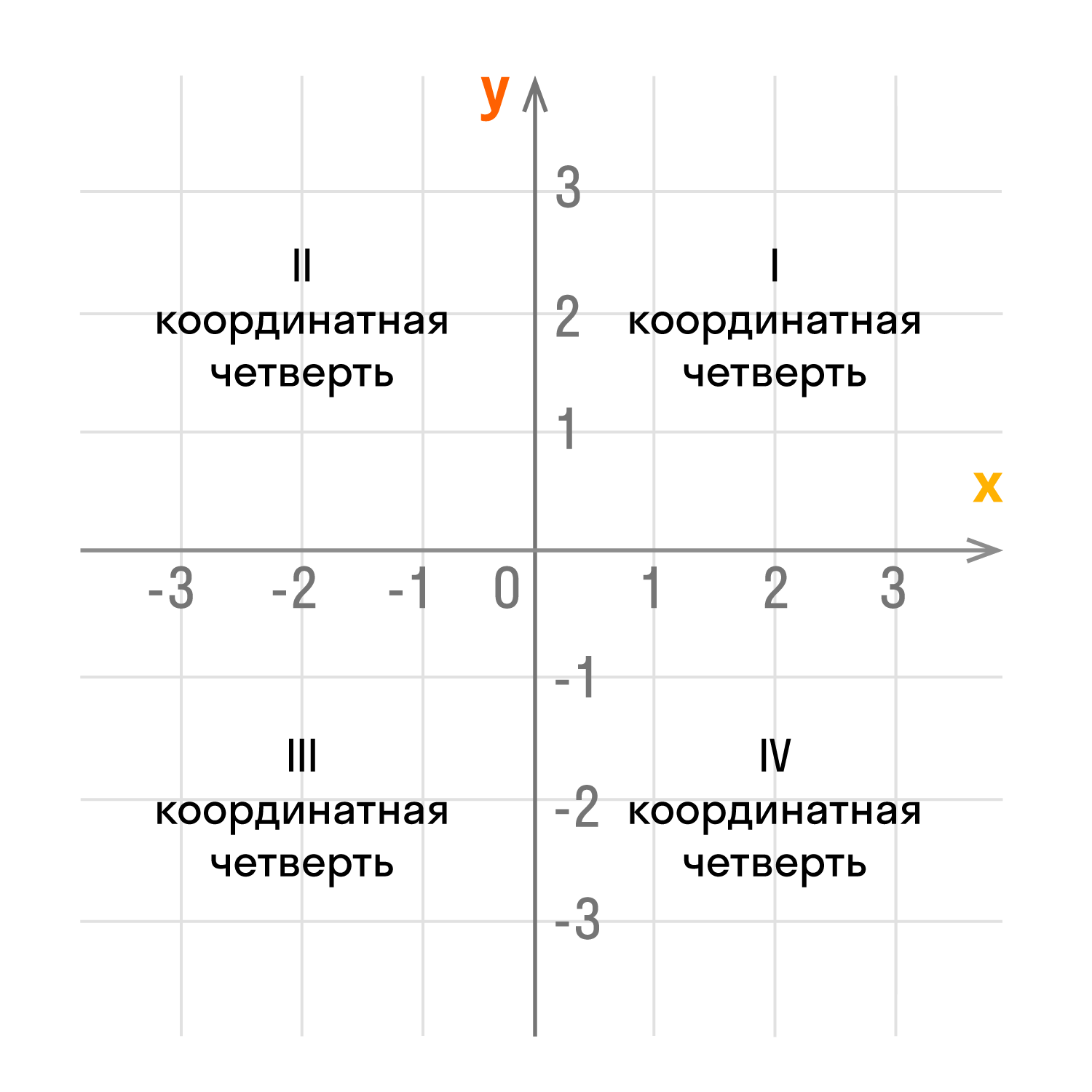
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Источник