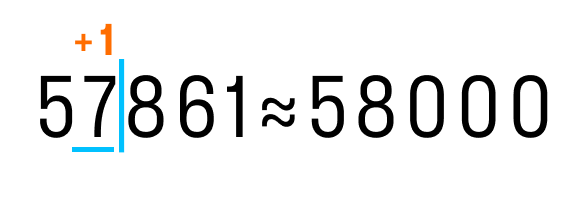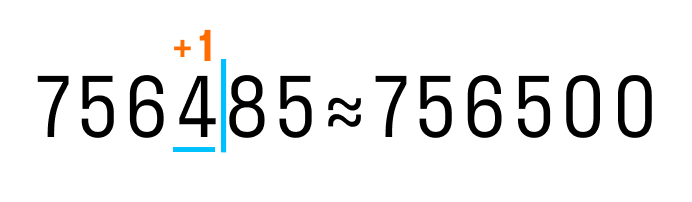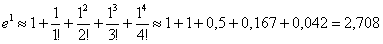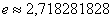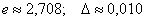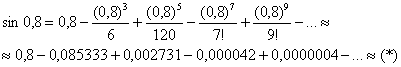Презентация на тему: Что означают слова «с точностью до …»
Что означают слова «с точностью до …» МОУ ООШ дер. Старое Мелково Учитель: Костик Инна Станиславовна
Что означают слова «с точностью до … Цель : ввести запись a ± h; способствовать усвоению терминологии; развивать навыки определения по записи промежутка, которому принадлежит точное значение величины
Что означают слова «с точностью до … Устная работа: Округлить до целых, десятых, сотых: 335,0894 ≈ 335,0894 ≈ 335,0894 ≈ 335,8594 ≈ 335,8594 ≈ 335,8594 ≈
Что означают слова «с точностью до …Устная работа: Округлить до целых, десятых, сотых: 335,0894 ≈ 335 335,0894 ≈ 335,1 335,0894 ≈ 335,09 335,8594 ≈ 336 335,8594 ≈ 335,9 335,8594 ≈ 335,86
Что означают слова «с точностью до …Сообщение диктора « 79% избирателей собираются на выборах отдать свои голоса за кандидата А. Погрешность этого результата не превосходит 5%» Что это означает? В действительности процент избирателей может отличаться от 79% в ту или иную сторону не более, чем на 5%, т.е. он содержится в промежутке 74% ≤ х ≤ 84% х = 79% ± 5%
Что означают слова «с точностью до …А как перейти от двойного неравенства к записи с помощью знака ± ? Для этого надо взять середину данного промежутка и найти расстояние от середины до его концов. Например: 46% ≤ х ≤ 52% а = (46 + 52)/2 = 49 h = 49 – 46 = 3 или h = 52 – 49 = 3 х = 49% ± 3%
Что означают слова «с точностью до …Значения величин в справочной и технической литературе указываются таким образом, что по записи можно судить о точности приближения. Например: Плотность меди ρ равна 8,96 г/см³ т.е. ρ =8,96 ± 0,01 г/см³ Масса Земли равна 5,976 · 10²⁴ кг, т.е.
Относительная точностьВажная характеристика приближённого значения величины – относительная точность. Она позволяет судить о качестве приближения. Например: Толщина
Относительная точностьКакое измерение точнее? 0,01/0,15 ≈ 0,067 – это 6,7% 500/384000 ≈ 0,001 – это 0,1% Первое приближение получено с относительной точностью до 6,7%, а второе – с относительной точностью до 0,1%
Закрепление изученного материала № 147, 148, 150
Самостоятельная работа Вариант 1 Вариант 2 Замените равенство двойным неравенством а) х = 26±0,6; а) у = 34±0,4; б) а = 2,6±0,6; б)
Проверка Вариант 1 Вариант 2 Замените равенство двойным неравенством а) 25,4 ≤ х ≤ 26,6; а) 33,6 ≤ у ≤ 34,4; б) 2 ≤ а ≤ 3,2; б) 3,3 ≤
Домашнее задание § 1.6 № 152(б), № 153(а – в), № 157
Итог урока Что означает запись a ± h? Как от записи с помощью знака «±» перейти к двойному неравенству? Как от двойного неравенства перейти к записи с помощью знака «±»? Что называется относительной точностью?
Спасибо за урок!
Чтобы скачать материал, введите свой email, укажите, кто Вы, и нажмите кнопку
Нажимая кнопку, Вы соглашаетесь получать от нас email-рассылку
Если скачивание материала не началось, нажмите еще раз «Скачать материал».
Источник
Правильное округление чисел
О чем эта статья:
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
- Наименьшее натуральное число: единица (1).
- Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
- У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.
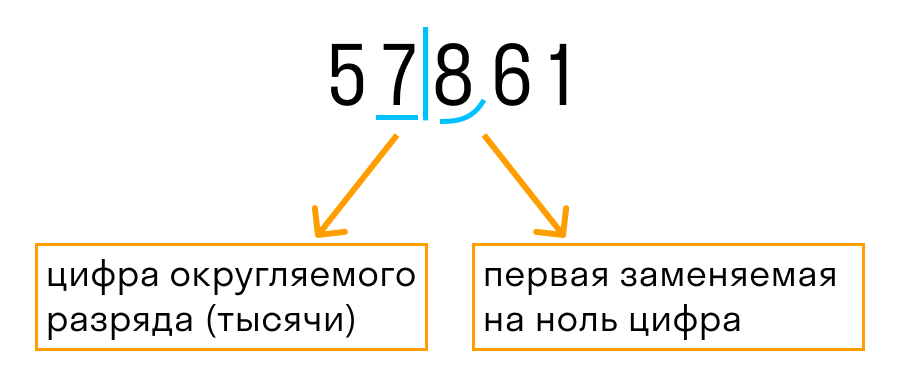
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
- как округлить число 697 до десятков — 697 ≈ 700;
- как округлить число 980 до сотен — 980 ≈ 1000.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
- 7 882 000 = 7 882 тыс.
- 1 000 000 = 1 млн.
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных.
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
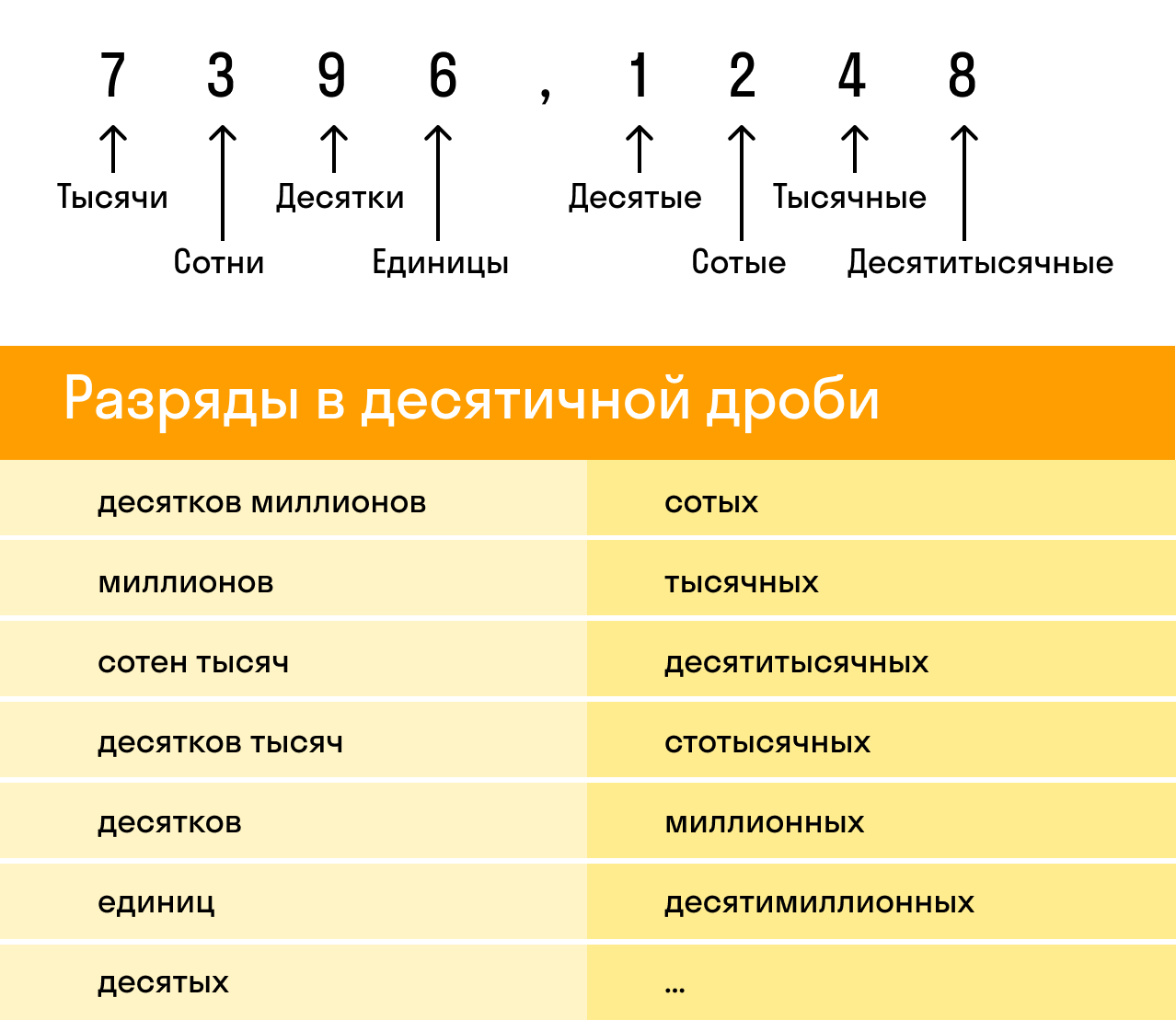
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
- не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
- увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Источник
Приближенные вычисления с помощью рядов
После изучения основных понятий функциональных и степенных рядов, задачи разложения функций в ряды переходим к обширной группе приложений рассматриваемой темы. К основным заданиям, которые часто встречаются на практике, относятся следующие:
– приближённое вычисление значения функции с помощью ряда;
На данном уроке мы рассмотрим первую, наиболее простую задачу, для решения которой потребуются самые элементарные знания о рядах, таблица разложений функций в степенные ряды и микрокалькулятор. Как вариант, пойдёт Эксель (если умеете управляться с его функциями). Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:
Существует 2 типа рассматриваемой задачи, с которыми мы на самом деле уже сталкивались ранее, в частности при вычислении интеграла по формуле трапеций и методом Симпсона. Тип первый:
Используя разложение функции в ряд, вычислить число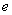 
, ограничившись 5 членами разложения. Результат округлить до 0,001. Провести вычисления на калькуляторе и найти абсолютную погрешность вычислений.
Решение: прежде всего, выбираем подходящее табличное разложение функции. Очевидно, что в нашем случае необходимо взять следующий ряд: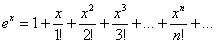 
, который сходится при любом значении «икс».
Кратко повторим, что такое сходимость функционального ряда: чем больше слагаемых мы рассмотрим, тем точнее функция-многочлен будет приближать функцию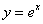 
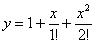
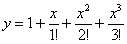
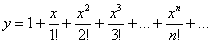
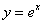
. Действительно, график параболы 
совсем не напоминает экспоненту и график кубической функции 
тоже далёк от идеала, но если взять 50-100 членов ряда, то картина в корне поменяется. И, наконец, график бесконечного многочлена 
совпадёт с графиком экспоненциальной функции 
.
Примечание: в теории даже есть такой подход и определение: функция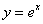 
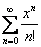
– это сумма функционального ряда 
.
В условии прямо сказано, что нужно просуммировать 5 первых членов ряда, причём, результат следует округлить до 0,001. И поэтому проблем здесь никаких: 
Вычислим более точное значение с помощью микрокалькулятора: 
Абсолютная погрешность вычислений:
– ну что же, вполне и вполне неплохо. Но бывает лучше.
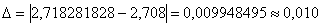
Ответ: 
Теперь рассмотрим нескольку другую разновидность задания:
Используя разложение функции в ряд, вычислить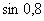 
приближённо с точностью до 0,001.
! Примечание: иногда аргумент бывает выражен в градусах, в таких случаях его необходимо перевести в радианы.
Давайте вспомним смысл выражения «с точностью до 0,001». Оно обозначает, что наш ответ должен отличаться от истины не более чем на 0,001.
Решение: используя табличное разложение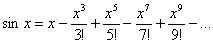 
, запишем несколько членов соответствующего ряда, при этом округление лучше проводить с «запасом» – до 5-6 знаков после запятой: 
Сколько членов ряда следует просуммировать для достижения требуемой точности? Для сходящихся знакочередующихся рядов справедлив следующий критерий: члены следует суммировать до тех пор, пока они по модулю больше заданной точности. Первый же меньший вместе со всем «хвостом» подлежит утилизации. В данном примере таковым является 4-й член: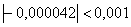 
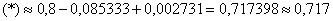
, поэтому:
– с округлением финального результата до требуемой точности.
Ответ: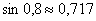 
с точностью до 0,001
Наверное, все понимают, почему она гарантирована: здесь к отрицательному 4-му члену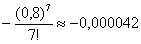 
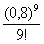
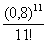
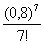
прибавляется мЕньшее по модулю число 
, затем из результата вычитается ещё более малое число 
– и так далее до бесконечности. Образно говоря, конструкция напоминает маятник с затухающими колебаниями, где 
– самый большой размах в отрицательную сторону, «затмевающий» собой все остальные движения.
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Tutoronline.ru – онлайн репетиторы по математике и другим предметам
Источник
