Множество делителей что это значит

Что такое множество?

Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.

Например: множество школьников, множество машин, множество чисел .

В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео , то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F ( friends ), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

Пример 2 . Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈ . К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D ). Записывается это так:

Читается как «2 принадлежит множеству делителей числа 6»

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉ . К примеру, делитель 5 не принадлежит множеству D . Записывается это так:

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

Зададим множество, которое состоит из одного числа 2

Зададим множество, которое состоит из двух чисел: 2 и 5

Множество натуральных чисел

Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.

Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.

В прошлых уроках, когда мы употребляли слово «число» , чаще всего подразумевалось именно натуральное число.

В математике множество натуральных чисел обозначается заглавной латинской буквой N.

Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N

Читается как: «единица принадлежит множеству натуральных чисел»

Множество целых чисел

Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.

Множество целых чисел обозначается заглавной латинской буквой Z .

Укажем, к примеру, что число −5 принадлежит множеству целых чисел:

Укажем, что 10 принадлежит множеству целых чисел:

Укажем, что 0 принадлежит множеству целых чисел:

В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.

Множество рациональных чисел

Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.

Рациональное число — это число, которое может быть представлено в виде дроби , где a — числитель дроби, b — знаменатель.

В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).

Например, представим, что вместо a стоит число 10, а вместо b — число 2

10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби 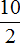, а значит число 5 входит во множество рациональных чисел.

Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.

Теперь представим, что вместо a стоит число 12, а вместо b — число 5.

12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби 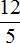, а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.

Мы вычислили дробь 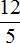и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:

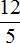
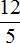
При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.

В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:

• целые числа
• обыкновенные дроби
• десятичные дроби
• смешанные числа

Множество рациональных чисел обозначается заглавной латинской буквой Q.

Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:

∈ Q

Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:

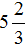
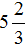
Укажем, что смешанное число принадлежит множеству рациональных чисел:

∈ Q

Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

12 thoughts on “Что такое множество?”

В первой части во втором примере вы написали что 5 не принадлежит D ,но в объяснение написали что «2 не принадлежит множеству делителей числа 6″. Поправьте ошибку.

Источник

Число простых делителей числа. Сколько делителей имеет простое число?

Каждый школьник знает, что все числа делятся на простые и составные. Более того, тем, кто усердно изучает математику, известны и их свойства. Однако если ответ на вопрос, сколько делителей имеет простое число, скрыт в самом определении этого понятия, то выяснить количество простых делителей для заданного — достаточно сложная задача. Она решается с применением метода перебора и вероятностных алгоритмов, реализуемых на ЭВМ.

Немного истории

Достоверно известно, что серьезным изучением свойств простых чисел первыми стали заниматься древние греки. Однако об их существовании было известно за несколько тысячелетий до того, как Аристотель включил теоремы об их свойствах в свои знаменитые “Начала”. Древние греки придумали и решето Эратосфена, представляющее собой алгоритм нахождения простых чисел из промежутка [1,n].

В 17 веке прорыв в их изучении сделали Пьер Ферма и Марен Мерсенн. Первый сформулировал теорему, впоследствии названную его именем, согласно которой все числа вида 2 2n — простые, доказав ее для n =1..4. Однако впоследствии Леонардом Эйлером было показано, что при n=5 получается составное число. Параллельно с этим Марен Мерсенн выделил простые числа вида 2 p — 1, в которых p – простое. Они интересны тем, что для них легко проверить соответствие критерию простоты. Учитывая этот факт, числа Мерсенна используют для выявления сверхбольших простых чисел. На данный момент предельное из известных выглядит как 2 77232917 − 1 .

Кроме того, их широко используют при создании генераторов случайных чисел, имеющих широкое применение на практике.

Большую роль в исследовании простых чисел сыграли также Лежандр и Гаусс. Эти ученые выдвинули гипотезу об их плотности.

Решето Эратосфена

Если можно сразу же назвать простые делители числа 4, то для больших чисел сделать это обычно достаточно затруднительно. О решении этой проблемы люди стали задумываться еще несколько тысячелетий назад. В частности, древнегреческий математик Эратосфен, живший на стыке третьего и второго веков до Рождества Христова придумал алгоритм нахождения всех простых чисел, меньших целого числа n.

Он получил название решета, так как «просеивает» или по-современному «фильтрует» все числа, кроме простых.

Алгоритм состоит из следующих команд:

1. выписать все целые числа от 2 до n;
2. присвоить переменной p значение 2, так как это наименьшее простое число;
3. зачеркнуть в списке все числа от 2p до n, кратные p;
4. присвоить значению переменной p значение первого, не зачеркнутого числа записанной последовательности, которое большее p;
5. повторять 3-й и 4-й, пока возможно.

Если все сделано правильно, то в списке останутся не зачеркнутыми все простые числа от двух до n.

Для реализации решета Эратосфена на электронно-вычислительной машине используют модернизированный алгоритм. На 3-м шаге можно зачеркивать числа, начиная с числа p₂, так как все составные числа, которые меньше него, к этому времени уже будут зачеркнуты. Тогда остановка работы алгоритма должна произойти, когда выполнится условие p₂>n.

Следует также учесть, что все простые числа, за исключением двойки, — нечетные, поэтому, начиная с p2 можно «фильтровать» по 2p.

Основная теорема арифметики

Согласно определению, простое число имеет два делителя. Один из них — 1, а второй — сама эта величина.

Прежде чем выяснить, каково число простых делителей числа, стоит уделить немного времени изучению основной теоремы арифметики. Согласно ей, натуральное число n > 1 можно представить, как n = p₁*… ⋅*p_k, где p₁, … , p_m — простые числа. При этом такое представление является единственным с точностью до порядка следования его сомножителей.

Следствие этой теоремы можно сформулировать следующим образом: любое натуральное число n представимо в виде n = p₁ d1 *p₂ d2 * …* p_k d m (в другой формулировке: каноническое разложение числа n на простые сомножители имеет вид n = p₁ d1 *p₂ d2 *⋅ …⋅*p_k d m ), где p₁

Кроме того, уже известную вам основную теорему арифметики можно перефразировать следующим образом: любое каноническое разложение n можно считать тождественным, если не обращать внимания на порядок делителей. Это значит, что на практике для значительной части чисел существует множество достаточно простых алгоритмов их разложения на простые множители, которые в итоге дают один и тот же результат.

Критерий простоты

Прежде чем выяснить, как можно найти наибольший простой делитель числа (НПД) n, следует разобраться с другим важным вопросом.

Итак, выясним, по какому алгоритму можно установить, есть ли у величины другие делители кроме единицы и его самого.

Сделать это можно путем перебора простых чисел p₁, …p_k. Причем завершить цикл можно, как только p_i+1, для которого производилась проверка, будет удовлетворять условию (pi₊₁) 2 > n.

Дадим объяснение, почему перебор можно ограничить p_i>=sqr(n).

Предположим, у числа n, исследуемого на простоту есть некоторый делитель p. Тогда d=n/p так же будет его делителем. Но, так как d и p — разные числа, ни один из них не может быть больше корня из n.

Как найти наибольший простой делитель числа n

Найти НПД n, можно, действуя по следующей схеме:

• Разделить n на два, если оно четное или на три, если нечетное. Исключение составляет n, последняя цифра в десятичной записи которого ноль или пять. Такое число можно сразу разделить на пять.
• Если результат не целое число, то делят n на следующие целые числа, перебирая их вплоть до p_i>=sqr(n).

Над получившимся числом n₁ производят все действия, в том же порядке, что представлен выше, только с условием p_i>=sqr(n₁).

Если же ни на одном из шагов перебора n₁ не делится на одно из простых чисел, то n целое и является своим же НПД. В противном случае получаем n₂ и продолжаем деление с перебором до момента, когда на (i+1) шаге установим, что n_i — целое.

Пример

Найдем простые делители числа 276.

• делим на «два»;
• получаем 138;
• так как число четное, то вновь делим на «два»;
• результат — 69;
• делим на следующее простое число «три»;
• получаем 23.

Так как это число простое, можем подвести итог. Простыми делителями 276 являются 2, 3 и 23.

Как найти число простых делителей числа

Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.

• 54 делим на «два» и получаем 27;
• 27 нечетное, поэтому разделим его уже не на «два», а на следующее простое число, т. е. «три»;
• заметим, что 27=3 3 ;
• таким образом, разложение 54 имеет вид 54 = 2 1 * 3 3 , т.е. простые делители числа 54 — это «два» и «три».

Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p₁* d1 p₂ d2 *⋅ …⋅*p_m d m , увеличенных на 1. Иными словами, в общем случае K = (d₁+1)*. * (d_m+1).

Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.

Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.

Пример

Найти число простых делителей числа 9990.

• так как число 9990 заканчивается на цифру «ноль», то оно делится на пять и на два.
• имеем 999.
• в результате деления на три имеем 333;
• снова делим на три, получаем 111;
• делим на три, имеем 37;
• 37 простое число, так как не делится без остатка ни на одно из простых чисел, которые находятся между двойкой и корнем из числа 37;
• подсчитываем количество простых делителей числа 9990. Это 2,3,5 и 37, то есть всего их четыре.

Проблема больших чисел

Как не странно, задача нахождения всех простых множителей числа является достаточно сложной. Дело в том, что до сих пор мы рассматривали только числа, десятичная запись которых состояла из одного-четырех знаков. Для них все вычисления выполняются в несколько шагов и их вполне можно осилить, имея под рукой лишь ручку и лист бумаги. По-другому обстоит дело, когда речь идет о, например, 1000-значном числе. Чтобы найти все его простые множители потребуется больше миллиарда лет, если даже будет задействован самый мощный суперкомпьютер в мире.

Простые числа и защита информации

Каждый современный человек, который пользуется возможностями, которые возникли благодаря появлению локальных компьютерных сетей и Интернета, нуждается в защите конфиденциальности своих личных данных, электронной переписки и пр. С этой целью используются криптографические алгоритмы с открытым ключом.

В системах с десятками и сотнями пользователей управление ключами является серьезной проблемой. Чтобы предотвратить овладение злоумышленником ключевой информацией, необходимо введение в процесс шифрования некой случайной величины.

Для этой цели наиболее распространенные на данный момент алгоритмы RSA используют большие простые числа.

Существует всего 10151 простых чисел длиною 1 — 512 битов включительно. В то же время для чисел, которые близки к n, вероятность того факта, что случайно выбранное число будет простым, — 1/ln n. Таким образом, полное количество простых чисел, которые меньше n равно n/ln n. Это позволяет считать, что крайне маловероятно, что 2 человека выберут одно и то же большое простое число.

Тест Миллера — Рабина

В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.

Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.

Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2 s t.

Затем выбирается случайное число a, такое что 1

Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4 -r ).

Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.

Источник