Просто и доступно о матрицах. VI
Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
15. Обращение линейного преобразования в простейшем случае.
Чтобы обратить линейное преобразование, нужно, чтобы число аргументов было равно числу функций.
Вот простейший пример, когда это требование нарушается:
Зная аргументы, можно однозначно вычислить функцию. А, наоборот, однозначно восстановить аргументы по значениям функции невозможно.
На языке матриц это означает, что обращение допускают лишь квадратные матрицы.
Рассмотрим вопрос об обращении матриц подробнее.
Пусть дано линейное преобразование
преобразующее пару чисел в пару чисел . Соответствующая матрица имеет вид:
Возникает вопрос, возможно ли обратное преобразование
Чтобы ответить на этот вопрос, умножим первое уравнение на , а второе уравнение на , а затем исключим из формул линейного преобразования:
Аналогично, умножая первое уравнение на , а второе уравнение на и исключая из формул, получаем:
Итак, обратное преобразование имеет следующий вид:
Отсюда понятно, что обратное преобразование возможно, при условии, что некоторое число, а именно, .
Это число называется определителем или, иначе, детерминантом матрицы и, в отличие от матрицы, которая изображается с круглыми скобками, определитель ограничен двойными прямыми линиями, но чаще всего одиночными прямыми линиями:
Итак, обратное преобразование принимает вид:
Отсюда получаем обратную матрицу:
16. Правила вычисления определителей.
А теперь сформулируем правила вычисления определителей, которые понадобятся в дальнейшем.
Правило вычисления определителя второго порядка для квадратной матрицы 2х2
К понятию определителя третьего порядка можно прийти, рассматривая линейное преобразование с тремя аргументами и тремя функциями, подобно тому, как только что было обращено линейное преобразование с двумя аргументами и двумя функциями. Вычисления довольно громоздкие, поэтому они опущены.
Оказывается, что определитель третьего порядка представляет собой выражение:
Столь громоздкую формулу для вычисления определителя 3-го порядка можно восстановить с помощью правила Саррюса:
Согласно этому правилу есть три слагаемых со знаком плюс:
— произведение элементов, расположенных на главной диагонали , т.е. диагонали, направленной от левого верхнего угла к правому нижнему углу,
— два произведения элементов, расположенных по ходу треугольников, одна из сторон которых параллельна главной диагонали.
Ещё три слагаемых, берутся со знаком минус; они получаются аналогично, исходя из второстепенной диагонали.
Определители более высоких порядков вычисляются приведением по определённым правилам, которые мы здесь не изучаем, к определителям более низкого порядка. В конечном итоге все определители сводятся к определителям второго и третьего порядка.
Более подробно обращение матриц, правила вычисления определителей высоких порядков мы изучать не будем. Потому что в подавляющем большинстве случаев придётся обращать особые матрицы: ортогональные, унитарные. Их обращение сводится к применению довольно простых операций. А определители высоких порядков нам встречаться не будут.
17. Свойства обратных матриц.
Квадратная матрица называется невырожденной, если её определитель не равен нулю (Δ ≠ 0), и вырожденной, если он равен нулю (Δ = 0).
Выше был получен следующий результат: только невырожденные квадратные матрицы 2х2 допускают обращение.
Оказывается, что это свойство обратных матриц дословно обобщается на случай любых квадратных матриц.
Теперь возникает вопрос коммутирует обратная матрица с исходной, или нет?
Допустим, что не коммутирует, это значит, что для некоторой невырожденной квадратной матрицы существуют две обратные матрицы, и , такие, что
Умножим первое из этих выражений на :
Пришли к противоречию с исходной посылкой о неравенстве левой и правой обратных матриц.
Противоречие означает ложность исходной посылки.
Из того, что левая и правая обратные матрицы совпадают, следует, что обратная матрица коммутирует, т.е. перестановочна с исходной:
18. Две полезные теоремы.
18.1. Об определителе транспонированной матрицы.
Определитель матрицы в результате её транспонирования не менняется.
18.2. Теорема умножения определителей.
Det (AВ) = Det A · Det В
Определитель произведения двух матриц равен произведению определителей этих матриц. Данное утверждение очевидным образом обобщатся на случай любого числа матриц.
Эти теоремы нам понадобятся в дальнейшем. Что касается их доказательств, то очень простые доказательства мне неизвестны, поэтому теоремы придётся принять на веру.
Впрочем, истинность этих теорем в случае квадратных матриц второго порядка устанавливается непосредственно.
19. Похвальное слово линейной алгебре
В конечном итоге основательного знакомства с линейной алгеброй, где изучаются матрицы, определители, системы линейных уравнений, всевозможные линейные пространства и многие, многие другие полезные вещи, не избежать.
И вообще, линейная алгебра, наряду с математическим анализом, является базовым математическим курсом, которым должен хорошо владеть любой математик, физик и инженер.
Источник
Коммутирующие матрицы
В линейной алгебре две матрицы А <\ displaystyle A> 
а также B <\ displaystyle B> говорят, что ездят, если А B знак равно B А <\ displaystyle AB = BA> , или, что то же самое, если их коммутатор [ А , B ] знак равно А B — B А <\ displaystyle [A, B] = AB-BA> равно нулю. Набор матриц А 1 , … , А k <\ Displaystyle A_ <1>, \ ldots, A_ называется коммутирующими, если они коммутируют попарно, что означает, что каждая пара матриц в наборе коммутирует друг с другом.
- Коммутирующие матрицы сохраняют собственные подпространства друг друга . [1] Как следствие, коммутирующие матрицы над алгебраически замкнутым полемодновременно являются треугольными ; то есть есть основания, над которыми они оба являются верхнетреугольными . Другими словами, если А 1 , … , А k <\ Displaystyle A_ <1>, \ ldots, A_
> 
коммутируют, существует матрица подобия п <\ displaystyle P>такой, что п — 1 А я п <\ displaystyle P ^ <- 1>A_ P>верхний треугольник для всех я ∈ < 1 , … , k ><\ Displaystyle я \ в \ <1, \ ldots, к \>>. Обратное не всегда верно, так как следующие контрпример шоу: [ 1 2 0 3 ] [ 1 1 0 1 ] знак равно [ 1 3 0 3 ] ≠ [ 1 5 0 3 ] знак равно [ 1 1 0 1 ] [ 1 2 0 3 ] . <\ displaystyle <\ begin 1 & 2 \\ 0 & 3 \ end ><\ begin 1 & 1 \\ 0 & 1 \ end > = <\ begin 1 & 3 \\ 0 & 3 \ end > \ neq <\ begin 1 & 5 \\ 0 & 3 \ end > = <\ begin 1 & 1 \\ 0 & 1 \ end ><\ begin 1 & 2 \\ 0 & 3 \ end < bmatrix>>.>
Однако если квадрат коммутатора двух матриц равен нулю, т. Е. [ А , B ] 2 знак равно 0 <\ Displaystyle [А, В] ^ <2>= 0>, то верно обратное. [2]
- Если матрицы А <\ displaystyle A>а также B <\ displaystyle B>являются одновременно диагонализируемы ; то есть, если существует матрица подобия п <\ displaystyle P>такой, что п — 1 А п <\ displaystyle P ^ <- 1>AP>а также п — 1 B п <\ displaystyle P ^ <- 1>BP>оба диагональны , то А <\ displaystyle A>а также B <\ displaystyle B>добираться. Обратное не всегда верно, поскольку одна из матриц может быть недиагонализуемой. Например, [ 0 1 0 0 ] [ 1 0 0 1 ] знак равно [ 1 0 0 1 ] [ 0 1 0 0 ] но [ 0 1 0 0 ] не диагонализируется. <\ displaystyle <\ begin
0 & 1 \\ 0 & 0 \ end ><\ begin 1 & 0 \\ 0 & 1 \ end > = <\ begin 1 & 0 \\ 0 & 1 \ end ><\ begin 0 & 1 \\ 0 & 0 \ end ><\ text ><\ begin 0 & 1 \\ 0 & 0 \ end ><\ text <не диагонализуем.>>>
Если же обе матрицы диагонализуемы, то они могут быть диагонализованы одновременно.
- Если одна из матриц обладает тем свойством, что ее минимальный многочлен совпадает с характеристическим многочленом (т. Е. Имеет максимальную степень), что, в частности, происходит, когда характеристический многочлен имеет только простые корни , тогда другая матрица может быть записана как полином в первом.
- Как прямое следствие одновременной триангулируемости, собственные значения двух коммутирующих комплексных матриц A , B с их алгебраическими кратностями ( мультимножества корней их характеристических многочленов) могут быть сопоставлены как α я ↔ β я <\ Displaystyle \ альфа _ <я>\ leftrightarrow \ beta _ <я>>таким образом, что мультимножество собственных значений любого многочлена п ( А , B ) <\ Displaystyle P (А, В)>в двух матрицах — мультимножество значений п ( α я , β я ) <\ Displaystyle P (\ альфа _ <я>, \ бета _ <я>)>. Эта теорема принадлежит Фробениусу . [3]
- Две эрмитовы матрицы коммутируют, если их собственные подпространства совпадают. В частности, две эрмитовы матрицы без нескольких собственных значений коммутируют, если они имеют один и тот же набор собственных векторов. Это следует из рассмотрения разложения по собственным значениям обеих матриц. Позволять А <\ displaystyle A>а также B <\ displaystyle B>— две эрмитовы матрицы. А <\ displaystyle A>а также B <\ displaystyle B>имеют общие собственные подпространства, когда их можно записать как А знак равно U Λ 1 U † <\ displaystyle A = U \ Lambda _ <1>U ^ <\ dagger>>а также B знак равно U Λ 2 U † <\ displaystyle B = U \ Lambda _ <2>U ^ <\ dagger>>. Отсюда следует, что А B знак равно U Λ 1 U † U Λ 2 U † знак равно U Λ 1 Λ 2 U † знак равно U Λ 2 Λ 1 U † знак равно U Λ 2 U † U Λ 1 U † знак равно B А . <\ displaystyle AB = U \ Lambda _ <1>U ^ <\ dagger>U \ Lambda _ <2>U ^ <\ dagger>= U \ Lambda _ <1>\ Lambda _ <2>U ^ <\ dagger >= U \ Lambda _ <2>\ Lambda _ <1>U ^ <\ dagger>= U \ Lambda _ <2>U ^ <\ dagger>U \ Lambda _ <1>U ^ <\ dagger>= BA .>
- Свойство коммутации двух матриц не транзитивно : матрица А <\ displaystyle A>может ездить с обоими B <\ displaystyle B>а также C <\ displaystyle C>, И еще B <\ displaystyle B>а также C <\ displaystyle C>не ездят друг с другом. Например, единичная матрица коммутирует со всеми матрицами, которые между ними не коммутируют. Если набор рассматриваемых матриц ограничен эрмитовыми матрицами без кратных собственных значений, то коммутативность транзитивна как следствие характеризации в терминах собственных векторов.
- Теорема Ли , которая показывает , что любое представление о разрешимой алгебры Ли одновременно верхний triangularizable можно рассматривать как обобщение.
- П × п матрица А <\ displaystyle A>коммутирует с любой другой матрицей размера n × n тогда и только тогда, когда это скалярная матрица, то есть матрица вида λ я <\ displaystyle \ lambda I>, где я <\ displaystyle I>— единичная матрица размера n × n и λ <\ displaystyle \ lambda>является скаляром. Другими словами, центр из группы из п × п матриц относительно умножения является подгруппой скалярных матриц.
- Единичная матрица коммутирует со всеми матрицами.
- Каждая диагональная матрица коммутирует со всеми другими диагональными матрицами. [4]
- Жордановы блоки коммутируют с верхнетреугольными матрицами, которые имеют одинаковое значение вдоль лент.
- Если произведение двух симметричных матриц симметрично, они должны коммутировать.
- Циркулянтные матрицы коммутируют. Они образуют коммутативное кольцо, поскольку сумма двух циркулянтных матриц циркулянтна.
Понятие коммутирующих матриц было введено Кэли в его мемуарах по теории матриц, которые также обеспечили первую аксиоматизацию матриц. Первым значительным результатом, доказанным на них, был приведенный выше результат Фробениуса 1878 г. [5]
Источник
Операции над матрицами
Свойства операции сложения матриц
Для любых матриц А, В и С одного размера выполняются равенства:
1. А+В=В+А (коммутативность);
Произведением матрицы А = (aij) на число l называется матрица В = (bij) того же размера, что и матрица А, причем bij=l aij, «i,j.
Свойства операции умножения матрицы на число
2. l(А+В)=lА+lВ (дистрибутивность относительно сложения матриц).
3. (l+m)А=lА+mА (дистрибутивность относительно сложения чисел).
Произведением АВ матриц А и В (размеров m´n и n´r соответственно) называется матрица С размера m´r, такая, что сij= ai1 b1j+ a12 b2j+…+ aik bkj+…+ ain bnj=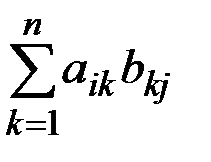 
.
Таким образом, каждый элемент сij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Получение элемента сij схематично изображается так
Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
1. (АВ)С=А(ВС)=АВС (ассоциативность).
2. (А+В)С=АС+ВС (дистрибутивность).
3. А(В+С)=АВ+АС (дистрибутивность).
4. АВ¹ВА (отсутствует коммутативность).
Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается А Т ).
1.3.1. Найти линейные комбинации заданных матриц:
а) А-lЕ,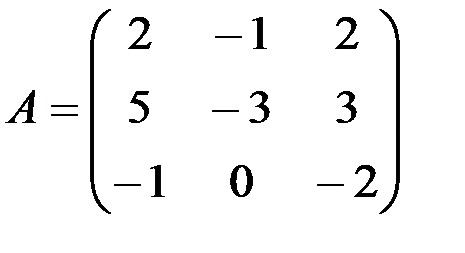 
;
б) 4А-5В,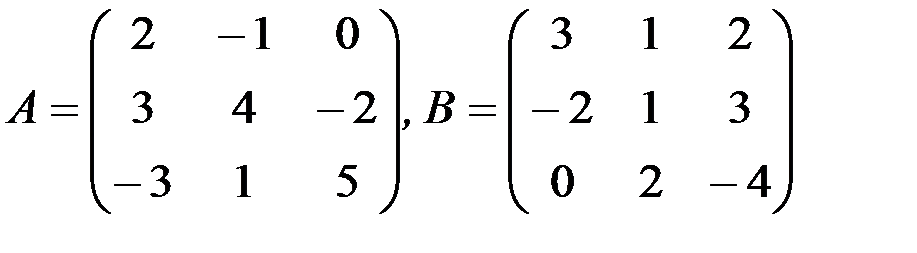 
.
1.3.2. Найти произведения матриц АВ и ВА (если они существуют):
а)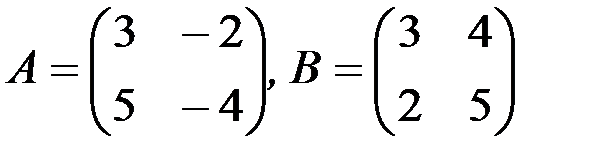 
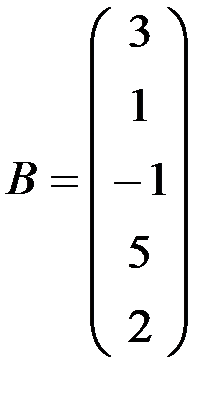
; б) А=(4 0 -2 3 1), 
;
в)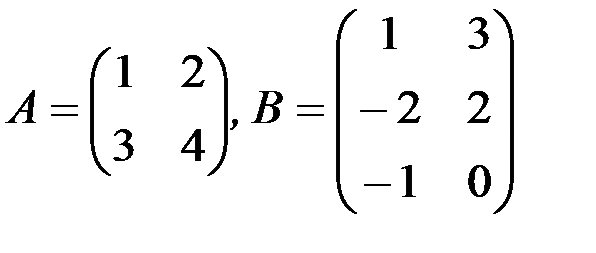 
.
1.3.3. Проверить, коммутируют ли матрицы:
а)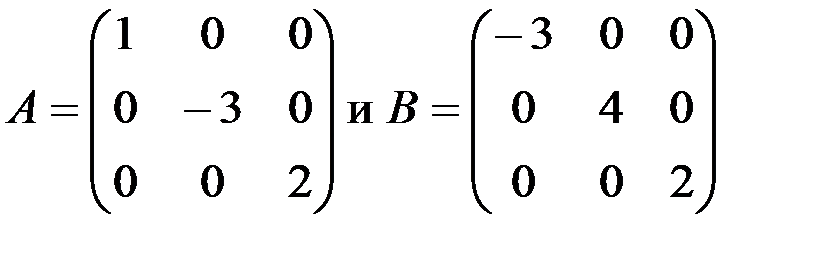 
;
б)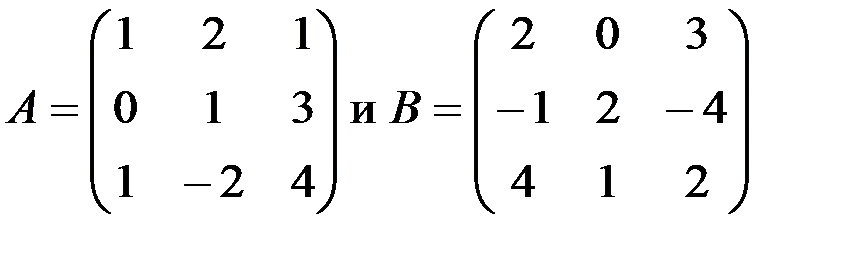 
.
1.3.4. Найти произведения матриц АА Т и А Т А:
а)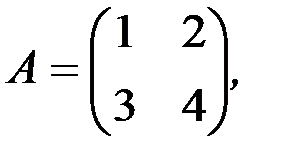 
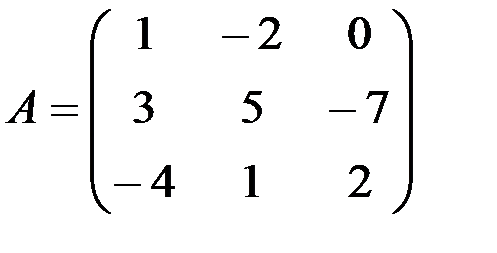
б) А=(1 2 3 4); в) 
.
1.3.5. Найти линейные комбинации матриц:
а) 5А-3В+2С,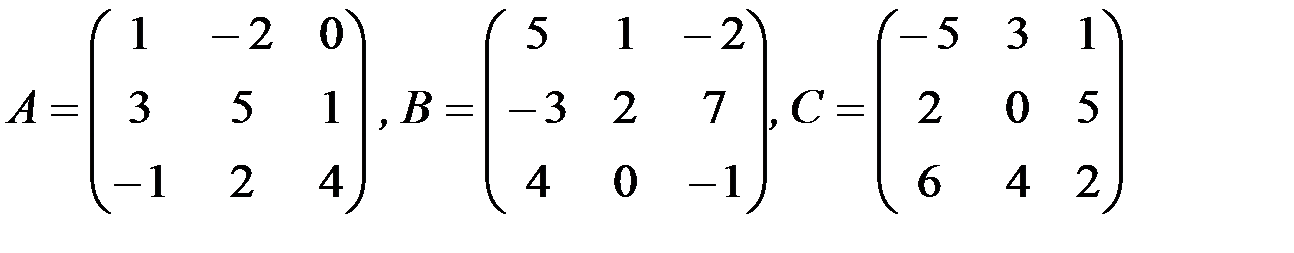 
;
б) А-lЕ,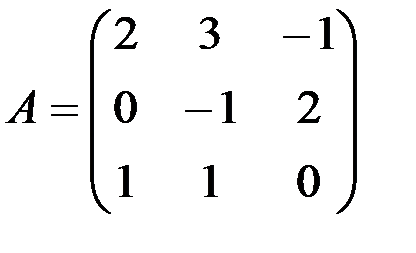 
.
1.3.6. Найти произведения АВ и ВА (если это возможно):
а)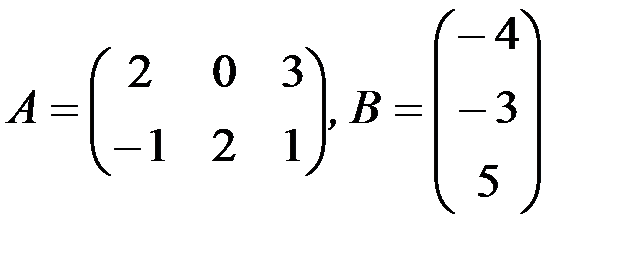 
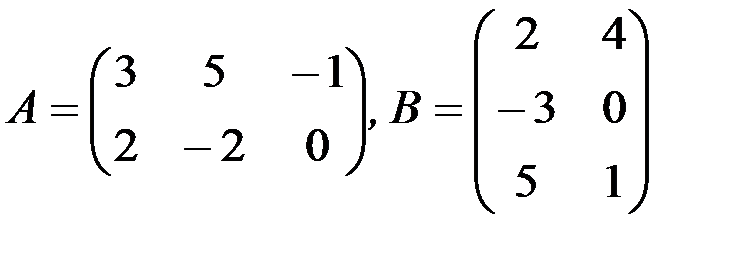
; б) 
.
1.3.7. Найти произведения АА Т и А Т А:
а)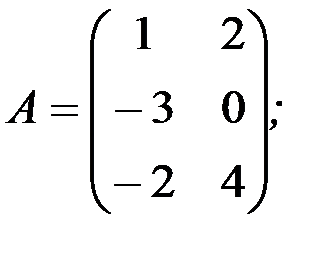 
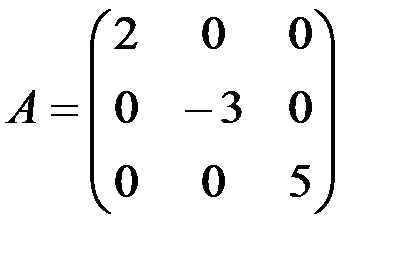
б) 
.
Ответы:
1.3.1.а)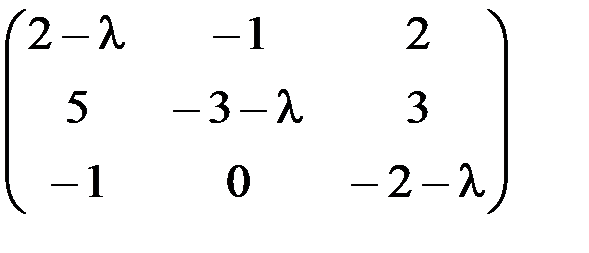 
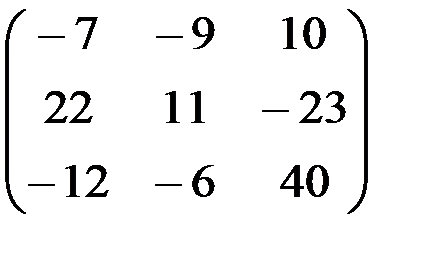
; б) 
.
1.3.2.а)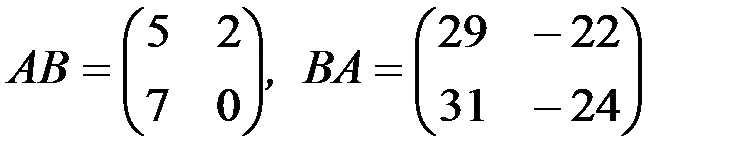 
;
б) АВ=(31); 
;
в) АВ не существует,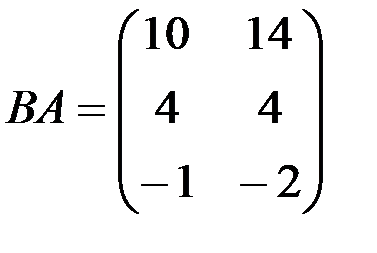 
.
1.3.4.а)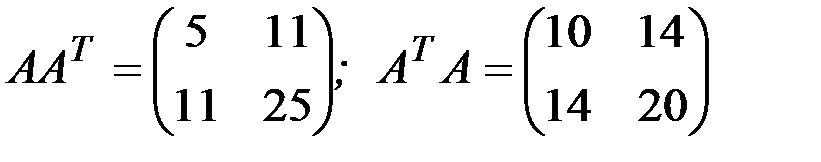 
;
б) АА Т =(30);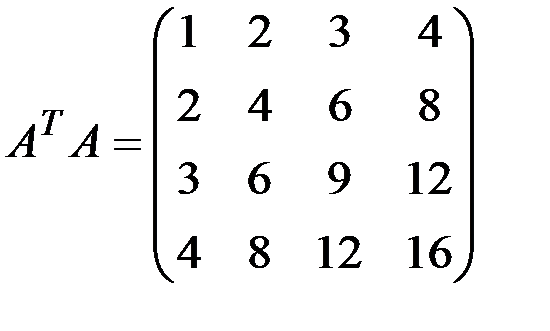 
;
в)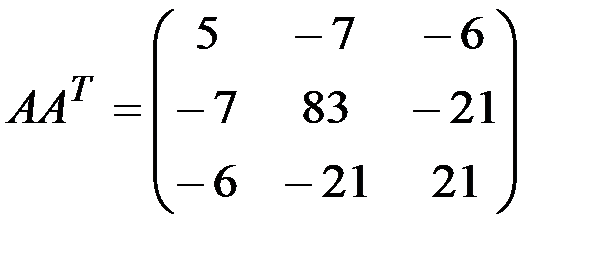 
; 
.
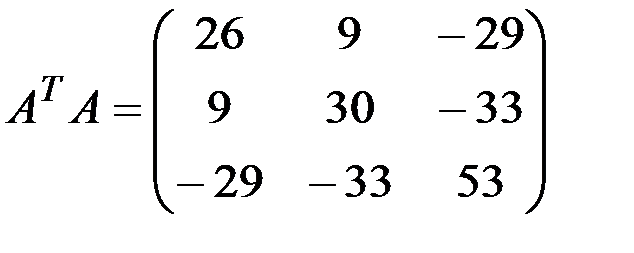
1.3.5.а)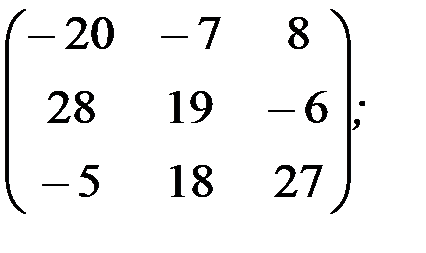 
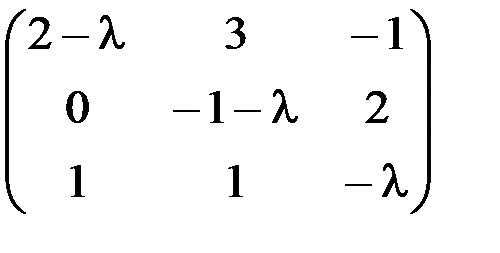
б) 
.
1.3.6.а)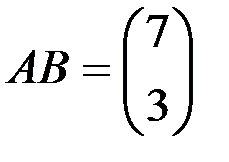 
, ВА – не существует;
б)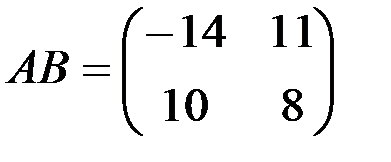 
; 
.
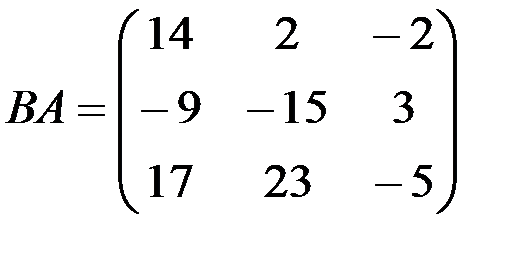
1.3.7.а)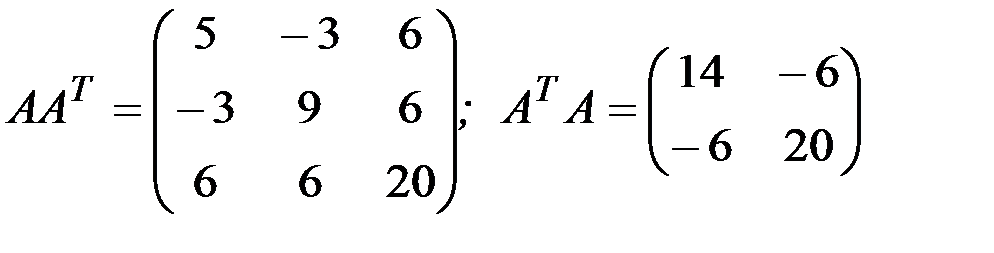 
;
б)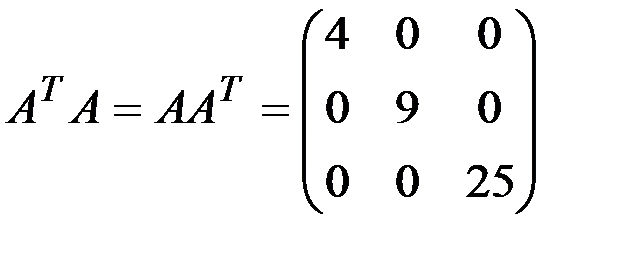 
.
Источник
