Математика 200 что это значит

По какой системе оцениваются результаты ГВЭ

Анастасия Зинченко

Некоторые школьники после 9 и 11 класса сдают итоговую аттестацию в формате ГВЭ. Баллы за этот экзамен выставляются и переводятся в оценки по особому принципу. Хотите разобраться? Из этой статьи вы узнаете, по какой системе оцениваются результаты ГВЭ.

Чем ГВЭ отличается от ОГЭ и ЕГЭ?

ГВЭ – это государственный выпускной экзамен. Его сдают школьники с ограниченными возможностями здоровья, дети-инвалиды, учащиеся закрытых учебных заведений и отбывающие наказание в исправительных колониях. Обязательно сдавать только ГВЭ по математике и русскому, остальные сдаются по желанию учащегося.

Подготовиться к экзаменам самостоятельно — очень непростая задача для ребенка. Если хотите готовиться быстрее и эффективнее, обратите внимание на онлайн-занятия с личным преподавателем MAXIMUM. Главная задача наших занятий — ваш максимальный результат. Мы выстраиваем личную стратегию подготовки к экзамену, и репетитор помогает вам каждый день приближаться к поставленной цели.

В какой форме сдают ГВЭ?

Как правило, такие экзамены сдаются в письменной форме. Задания на ГВЭ проще, чем на ОГЭ и ЕГЭ. Если по определенным причинам школьник не может писать, он имеет право сдавать ГВЭ устно. На сайте ФИПИ есть подробные правила по сдаче, а также пробные варианты экзаменов по всем дисциплинам и рекомендации сдающим.

Как оцениваются результаты ГВЭ?

Критерии оценивания ГВЭ отличаются от ОГЭ и ЕГЭ. Связано это с тем, что на ГВЭ задания упрощены. Однако, критериев оценивания больше: например, для слепых школьников задания будут одного формата, для глухонемых – другого.

Результаты экзамена оцениваются по балльной системе, баллы переводятся в школьные оценки — определенное количество баллов соответствует определенной оценке. Например, чтобы сдать ГВЭ в 9 классе, необходимо набрать количество баллов, которое соответствует тройке.

Внутри каждого экзамена есть разделение типов заданий для детей с разными особенностями. Рассмотрим подробнее русский язык и математику.

Система оценивания ГВЭ по русскому языку

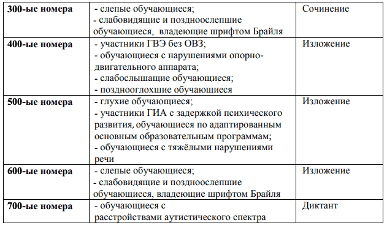
И в 9, и в 11 классе ГВЭ по русскому языку можно сдавать в форме сочинения, изложения и диктанта — об этом подробнее читайте здесь. Распределение заданий происходит по номерам, каждый из которых соответствует определенным отклонениям.

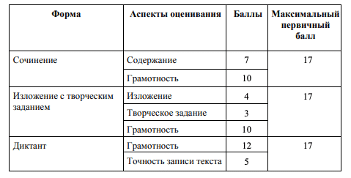
В документе ФИПИ представлена таблица критериев оценивания по каждому типу заданий по русскому языку.

Система оценивания ГВЭ по математике

Что касается математики, здесь система оценивания отличается от русского языка. Математика требует меньше усилий для письма и воспроизводства письменной речи — поэтому там меньше номеров для деления школьников по критериям.

В математике количество баллов и заданий различаются в зависимости от номера, присвоенного ученику. Участники ГВЭ с 100-ми номерами получают 10 заданий базового уровня с кратким ответом и еще 2 задания профильного уровня с развернутым ответом. Набрать можно 14 баллов в сумме.

Участники ГВЭ с 200-ми номерами получают 10 заданий с кратким ответом, где необходимо написать целое число или дробь. Максимум баллов, которое можно набрать – 10.

Участники ГВЭ с 300-ми номерами получают 12 заданий, где с 1 по 10 – это базовые задания, требующие краткого ответа, а 11 и 12 – развернутого. Макисмум баллов в данном случае – 14. Схожая система оценивания и на других предметах. Подробнее с ней можно ознакомиться в методических рекомендациях ФИПИ.

Теперь вы знаете, по какой системе оцениваются результаты ГВЭ. Несмотря на некоторые возможные ограничения, ГВЭ предусматривает все сложности, с которыми могут столкнуться школьники. Система оценивания подстроена под запросы как проверяющих, так и сдающих.

Если хотите быстро и эффективно подготовиться к экзаменам, обратите внимание на онлайн-занятия с личным преподавателем MAXIMUM. Мы выстраиваем программу личной подготовки к ЕГЭ, учитывая сильные и слабые стороны каждого ученика. Преподаватель не только проводит эффективные занятия, но и помогает ученикам поддерживать мотивацию и выполнять домашние задания. Пробный урок бесплатно!

Источник

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Кратное число — это .

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

1. Делимое – то число, которое собираются делить;
2. Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
3. Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

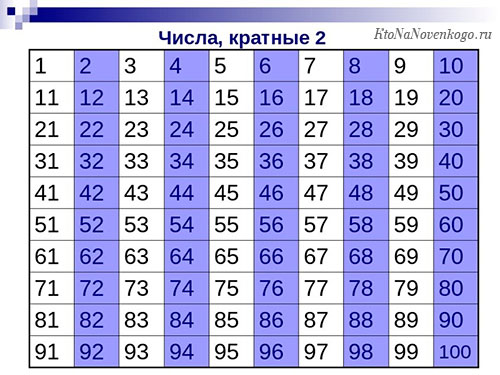
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

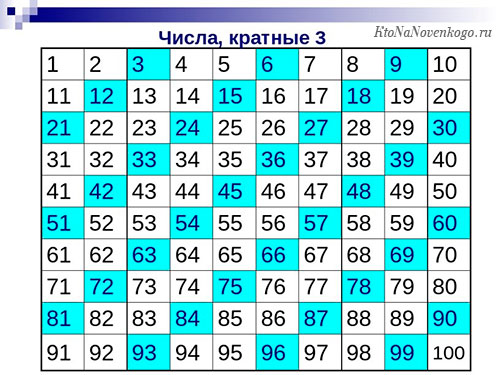
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

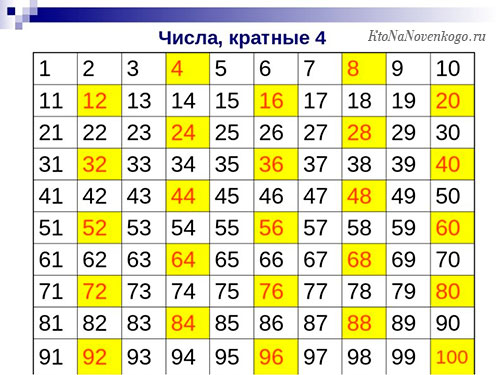
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

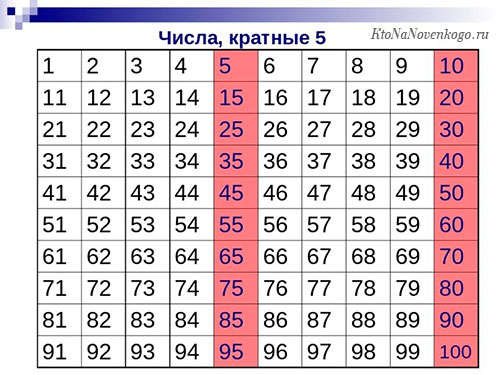
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

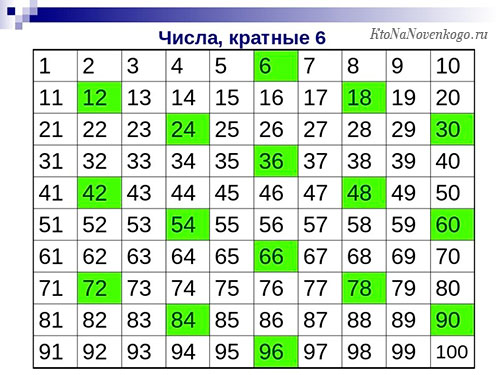
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

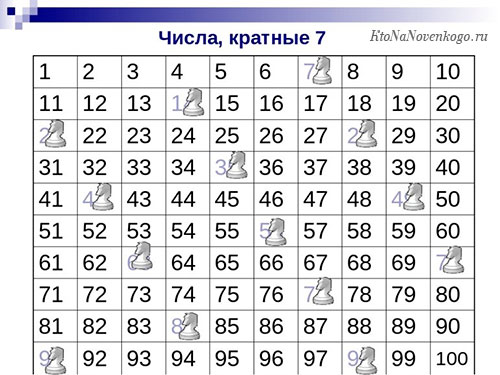
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Числа, кратные 9	27	198	5 877	3 816	117	72
Сумма	9	18	27	18	9	9

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Сумма разрядных слагаемых

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

• Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

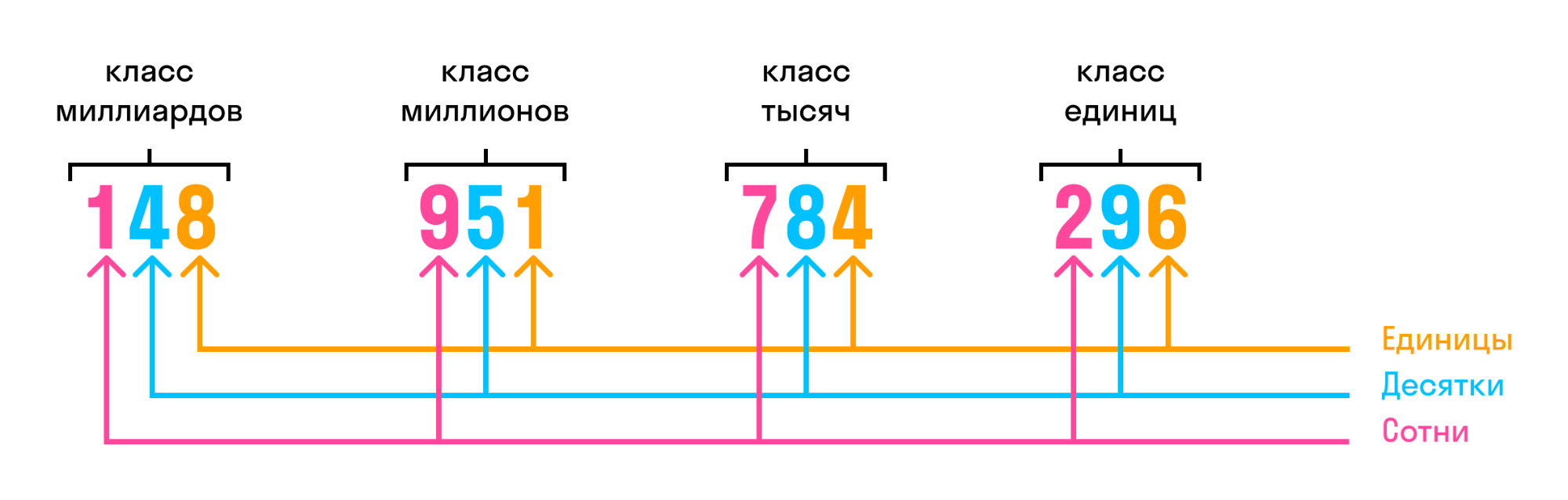
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

Названия классов многозначных чисел:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

• 345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

• Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

• 10 единиц = 1 десяток;
• 10 десятков = 1 сотня;
• 10 сотен = 1 тысяча;
• 10 тысяч = 1 десяток тысяч;
• 10 десятков тысяч = 1 сотня тысяч;
• 10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

• Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

• Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

• шести единиц миллионов (6 * 1 000 000);
• пяти десятков тысяч (5 * 10 000);
• семи единиц тысяч (7 * 1000);
• трех сотен (3 * 100);
• восьми десятков (8 * 10);
• шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

1. 84 610
   84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
   84 610 = 80 000 + 4 000 + 600 + 10.
2. 45 317
   45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
   45 317 = 40 000 + 5 000 + 300 + 17.
3. 56 789
   56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
   56 789 = 50 000 + 6 000 + 700 + 80 + 9.
4. 345 677
   345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
   345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
5. 687 543
   687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
   687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
6. 877 589
   877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
   877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

1. 4 895 634
   4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
   4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
2. 8 675 349
   8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
   8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
3. 77 897 125
   77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
   77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
4. 656 734 212
   656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
   656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Источник