Луч проходит между сторонами угла что это значит
В этом кратком справочнике поясняются понятия и теоремы, упоминаемые в книгах и задачах, опубликованных на нашем сайте. Справочник ни в кой мере претендует на полноту — это лишь необходимый комментарий к нашим задачам. Справочник формируется в соответствии с запросами наших читателей. Если Вас интересует, что означает данный термин, или что утверждает данная теорема, заполните форму, и мы ответим на Ваш вопрос. Знаком «*» помечены факты, относящиеся к данному понятию, знаком «-» помечены варианты формулировки определений.
Статьи на букву ‘Л’:
Шпернера
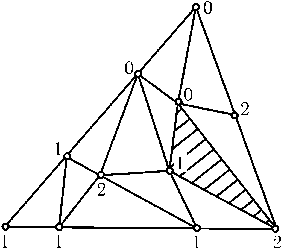
Рассмотрим треугольник, вершины которого помечены цифрами 0, 1 и 2, Разобъем этот треугольник на несколько треугольников так, чтобы никакая вершина одного треугольника не лежала на стороне другого. Вершинам исходного треугольника оставим старые пометки, а дополнительным вершинам припишем номера 0, 1, 2, причем так, чтобы любая вершина на стороне исходного треугольника была бы помечена одной из пометок вершин этой стороны (см. рис.). ( Лемма Шпернера ) утверждает, что в данной ситуации обязательно существует треугольник разбиения, помеченный цифрами 0, 1, 2. (См. задачу 58166.)
Ломаная
Ломаной A 1 A 2 A 3 . A n называется фигура, которая состоит из точек A 1 , A 2 , A 3 . A n ( вершин ломаной) и соединяющих их отрезков A 1 A 2 , A 2 A 3 , . A n — 1 A n ( звеньев ломаной). Длиной ломаной называется сумма длин её звеньев.
* Длина ломаной не меньше длины отрезка, соединяющего её концы.
- замкнутая
Ломаная называется замкнутой , если её концы совпадают.
- простая
Ломаная называется простой , если она не имеет самопересечений.
Луч
Лучом (или полупрямой ) называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки, которая называется начальной точкой , началом или вершиной данного луча.
Также часто говорят, что «луч исходит из данной точки», имея в виду, что эта точка является вершиной луча.
луч, проходящий между сторонами угла
Говорят, что луч проходит между сторонами угла , если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. В случае развёрнутого угла считается, что любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла.
* Если луч проходит между сторонами неразвёрнутого угла, то он пересекает любой отрезок с концами на сторонах угла.
лучи сонаправленные
Два луча (или, что то же самое, две полупрямые) называются одинаково направленными или сонаправленными , если существует параллельный перенос, который переводит один луч в другой.
Это эквивалентно тому, что либо два луча лежат на одной прямой, и один из лучей содержится в другом, либо два луча не лежат на одной прямой, но лежат в одной полуплоскости относительно прямой, проходящей через их начальные точки.
* Отношение сонаправленности лучей транзитивно: Если лучи a и b сонаправленны и лучи b и c сонаправлены, то лучи a и c также сонаправлены.
- лучи противоположно направленные
Два луча (или, что то же самое, две полупрямые) называются противоположно направленными , если прямые, на которых они лежат, параллельны или совпадают, и при этом лучи не являются сонаправленными.
Это верно тогда и только тогда, когда один из данных лучей сонаправлен с лучем, дополнительным к другому лучу.
Проект осуществляется при поддержке и .
Источник
Виды углов. Измерение углов
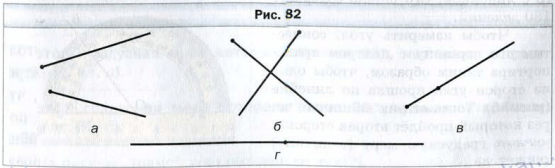
На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?
Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Угол, стороны которого образуют прямую, нахывают развернутым.
Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок ( 1 мм, 1 см и т.п.).
Однако для измерения углов мы пока не имеем такого единичного угла.
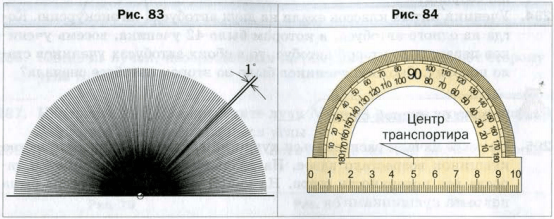
Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83 ). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат . gradus − » шаг», «ступенька») и записывают 1 °.
Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.
Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180 °.
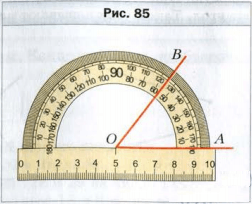
Для измерения углов используют специальный прибор − транспортир (рис. 84 ). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.
Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85 ).
Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.
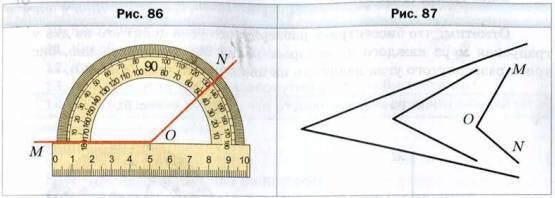
Так, на рисунке 85 градусная мера угла AOB равна 55 °. Пишут : ∠AOB = 55 °. На рисунке 86 имеем : ∠MON = 134 °.
Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.
Величина угла обладает следующим свойством.
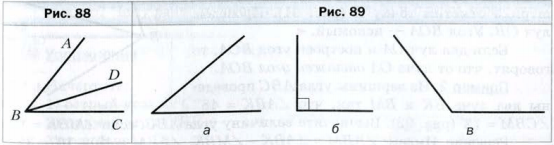
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88 ), т.е.
∠ABC = ∠ABD + ∠DBC.
Угол, градусная мера которого меньше 90 °, называют острым (рис. 89, a).
Угол, градусная мера которого равна 90 °, называют прямым (рис. 89, б).
На рисунке прямой угол обозначает так: ∟.
Угол, градусная мера которого больше 90 °, но меньше 180 ° называют тупым (рис. 89, в).
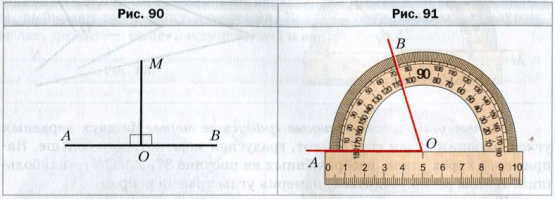
Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 °. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90 ).
Пример 1 . Дан луч OA. Постройте угол BOA, равный 72 °.
Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72 °. Возле этого штриха отметим точку B ( рис. 91 ). Проведем луч OB. Угол BOA − искомый.
Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.
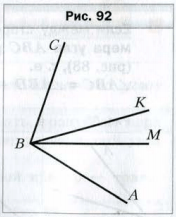
Пример 2 . Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48 °, ∠CBM = 72 ° (рис. 92 ).
Вычислите величину угла ABC, если ∠MBK = 16 °.
Имеем : ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48 ° − 16 ° = 32 °;
∠ABC = ∠ABM + ∠ С BM, ∠ABC = 32 ° + 72 ° = 104 °.
Источник
Виды углов. Измерение углов
На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?
Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Угол, стороны которого образуют прямую, нахывают развернутым.
Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок ( 1 мм, 1 см и т.п.).
Однако для измерения углов мы пока не имеем такого единичного угла.
Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83 ). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат . gradus − » шаг», «ступенька») и записывают 1 °.
Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.
Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180 °.
Для измерения углов используют специальный прибор − транспортир (рис. 84 ). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.
Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85 ).
Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.
Так, на рисунке 85 градусная мера угла AOB равна 55 °. Пишут : ∠AOB = 55 °. На рисунке 86 имеем : ∠MON = 134 °.
Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.
Величина угла обладает следующим свойством.
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88 ), т.е.
∠ABC = ∠ABD + ∠DBC.
Угол, градусная мера которого меньше 90 °, называют острым (рис. 89, a).
Угол, градусная мера которого равна 90 °, называют прямым (рис. 89, б).
На рисунке прямой угол обозначает так: ∟.
Угол, градусная мера которого больше 90 °, но меньше 180 ° называют тупым (рис. 89, в).
Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 °. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90 ).
Пример 1 . Дан луч OA. Постройте угол BOA, равный 72 °.
Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72 °. Возле этого штриха отметим точку B ( рис. 91 ). Проведем луч OB. Угол BOA − искомый.
Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.
Пример 2 . Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48 °, ∠CBM = 72 ° (рис. 92 ).
Вычислите величину угла ABC, если ∠MBK = 16 °.
Имеем : ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48 ° − 16 ° = 32 °;
∠ABC = ∠ABM + ∠ С BM, ∠ABC = 32 ° + 72 ° = 104 °.
Источник
Луч OA проходит между сторонами угла BOC.
Решение задачи указывает на некорректность её условия. Возможно, так и было задумано, чтобы найти в нём ошибку.
ВВ1 перпендикулярен плоскости альфа, следовательно, этот отрезок перпендикулярен любой прямой, проходящей в этой плоскости через В1.
BD=6√2 по условию.
∆ ВАD- прямоугольный равнобедренный. Его острые углы равны 45°⇒
AD=BD•sin45°=6
По условию AD лежит в плоскости α.
Поэтому по т. о 3-х перпендикулярах В1А⊥AD и C1D⊥DA, и проекция квадрата ABCD на эту плоскость – прямоугольник АВ1С1D.
Угол В1АD — прямой.
Проекция диагонали ВD на плоскость α – В1D и является гипотенузой
треугольника В1АD с прямым углом А.
B1D=AD:cos60°=6:1/2=12 (ед. длины)
Мы получили проекцию наклонной, которая имеет большую длину, чем сама наклонная ВD. Т.е. в прямоугольном ∆ ВВ1D длина катета B1D больше длины гипотенузы BD, чего быть не может.
а) величина угла В1DА равна 30°,то проекция ВD на плоскост α равна AD:cos30°=4√3.
б) угол В1DB=60° — В1D=3√2– тоже допустимый результат.
Источник