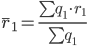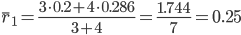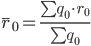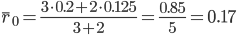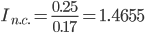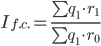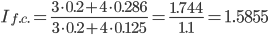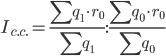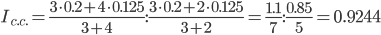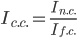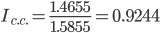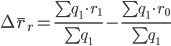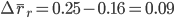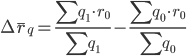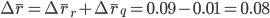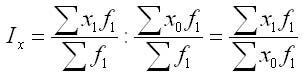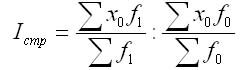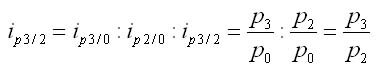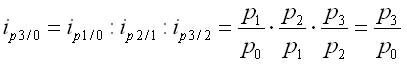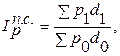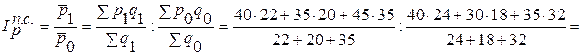Индекс переменного состава
При изучении качественных показателей часто приходится рассматривать изменение средней величины индексируемого показателя для определенной однородной совокупности. Будучи сводной характеристикой качественного показателя, средняя величина складывается как под влиянием значений показателя у отдельных единиц совокупности, так и под влиянием соотношения их весов («структуры совокупности»).
Пример №1 . Индекс переменного состава себестоимости продукции равен 1.1. Индекс фиксированного состава себестоимости продукции равен 0,95. Определите индекс структурных сдвигов себестоимости продукции, сделайте выводы.
Решение.
Ic.c = Iп.с./Iф.с. = 1,1/0,95 = 1,158
За счет изменения структуры себестоимости продукции, средняя себестоимости продукции выросла на 15,8%.
Пример №2 . Имеются следующие данные о затратах на продукцию и прибыли предприятия за два периода, млн. руб.
| Прибыль от реализации продукции. | Рентабельность затрат | ||
| базисный | отчетный | базисный | отчетный |
| 3 | 3 | 0,2 | 0,2 |
| 2 | 4 | 0,125 | 0,286 |
Определите абсолютное изменение средней рентабельности продукции в результате структурных сдвигов в затратах на производство и реализацию продукции.
Решение.
а) индекс рентабельности переменного состава
Рассчитаем средние рентабельности за каждый период:
Средняя рентабельность за отчетный период
Средняя рентабельность за базисный период
Соответственно, индекс рентабельностей переменного состава (индекс средних величин) будет представлять собой отношение:
За счет всех факторов рентабельность возросла на 46.55%.
б) индекс рентабельности фиксированного (постоянного) состава
За счет изменения структуры рентабельности средняя рентабельность возросла на 58.55%
в) индекс влияния изменения структуры прибыли на динамику средней рентабельности.
Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.:
За счет изменения структуры затрат средняя рентабельность снизилась на 7.56%
Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности.
Абсолютный прирост средних рентабельностей по всем группам будет рассчитываться следующим образом:
Изменение средней рентабельности по всем группам только за счет изменения средней рентабельности по отдельным группам будет рассчитываться по формуле:
Аналогичные рассуждения проводятся и для расчета изменения средней рентабельности по всем группам только за счет изменения структуры затрат:
Очевидно, что общий абсолютный прирост средних рентабельностей по всем группам равен сумме факторных изменений:
Источник
Индекс постоянного состава, Индекс структурных сдвигов
Для того чтобы устранить влияние изменения структуры совокупности на динамику средней величины, необходимо взять отношение средних взвешенных с одними и теми же весами. Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре совокупности, называется индексом постоянного состава и может быть вычислен по формуле:
Индекс постоянного состава говорит о том, как в отчетном периоде по сравнению с базовым изменилась средняя величина показателя по однородной совокупности за счет изменения только лишь самой индексируемой величины, т. е. когда влияние структурного фактора устранено.
Индекс структурных сдвигов
Индекс структурных сдвигов рассчитывается как отношение среднего уровня индексируемого показателя базисного периода, определенного на отчетную структуру, к фактической средней этого показателя в базисном периоде. Он нужен для измерения влияния только структурных изменений в исследуемый средний показатель.
Индекс структурных сдвигов рассчитывается по формуле:
Базисные и цепные индексы
В зависимости от основы сравнения индексы подразделяются на базисные и цепные.
Цепные индексы рассчитываются как отношение текущих уровней с предшествующим или непрерывно меняющейся базой сравнения.
Базисные индексы имеют постоянную базу сравнения — данные какого-то одного периода (анализ динамики), территории (территориальные сравнения) и планового задания (анализ выполнения плана).
Между цепными и базисными индивидуальными индексами существует зависимость:
1. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода определяется по формуле:
2. Произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода:
Индекс себестоимости продукции
Себестоимость продукции, работ, услуг представляет из себя важнейший показатель эффективности деятельности предприятия и стоимостную оценку используемых в процессе производства продукции природных ресурсов, топлива, сырья, трудовых ресурсов, материалов а также прочих затрат на ее производство и реализацию. Себестоимость продукции будет минимальной, при минимальной экономии материалов, энергии и т.д.
Индекс себестоимости продукции рассчитывается как изменение себестоимости единицы продукции отчетного периода по сопоставимому с базисным периодом кругу продукции.
Индекс себестоимости продукции определяется по формуле:
где числитель — затраты на производство продукции отчетного периода;
знаменатель — затраты на производство той же продукции при условии, что себестоимость продукции остается на уровне базисного периода.
Индекс себестоимости продукции определяет, во сколько раз уменьшился (возрос) в среднем уровень себестоимости на продукцию, произведенную в отчетном периоде, или сколько процентов составляет его снижение (рост) в отчетном периоде по сравнению с базисным.
Разность между числителем и знаменателем показывает перерасход (+) или экономию (—) в затратах от снижения себестоимости единицы продукции:
Источник
Индексы переменного и постоянного состава, индекс структурных сдвигов
Для изучения динамики качественных показателей (цена, себестоимость, производительность труда, средняя заработная плата и т. д.) определяют изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов:
· изменение значения индексируемого показателя у отдельных групп единиц;
· изменение структуры явления.
Для определения влияния каждого из этих факторов на общую динамику средней применяются индексы переменного, постоянного (фиксированного) состава и индекс структурных сдвигов.
Индексом переменного состава является индекс, отражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам.
Рассмотрим индекс цен переменного состава:
.
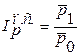
Отражает соотношение средней цены товаров в текущем и базисном периодах.
Поскольку средняя цена товаров определяется по формуле средней арифметической взвешенной как отношение товарооборота к объему продаж (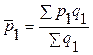
,
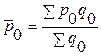
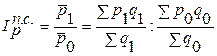
), то индекс цен переменного состава может быть записан следующим образом:
.
Если от объемов товара в натуральном выражении перейти к их удельным весам, то данный индекс может быть записан так:
где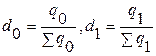 
– доля каждого товара соответственно в базисном и отчетном периодах.
Индекс постоянного (фиксированного) состава – характеризует динамику средней величины при одной и той же фиксированной структуре. Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т. е. когда влияние структурного фактора устранено.
Индекс цен фиксированного состава:
или 
– индекс цен фиксированного состава.
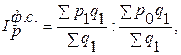
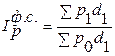
Индексом структурных сдвигов называется индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня изучаемого явления.
Индекс цен структурных сдвигов:
или 
– индекс цен структурных сдвигов.
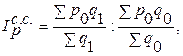
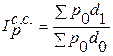
Взаимосвязь: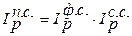 
.
Помимо мультипликативной модели, на основе индексов переменного, постоянного состава и структурных сдвигов может быть построено аддитивное разложение, отражающее абсолютное изменение среднего уровня качественного показателя за счет отдельных факторов.
Так, например, общий абсолютный прирост (уменьшение) средней цены товаров в целом по совокупности находится как разность числителя и знаменателя индекса цен переменного состава:
или 
.
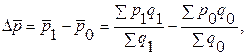
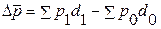
Абсолютный прирост (уменьшение) средней цены за счет изменения цен по отдельным единицам совокупности (например, по отдельным рынкам) определяется как разность числителя и знаменателя индекса цен фиксированного состава:
или 
.
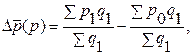
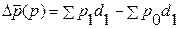
Абсолютный прирост (уменьшение) средней цены за счет структурных изменений рассчитывается как разность числителя и знаменателя индекса цен структурных сдвигов:
или 
.
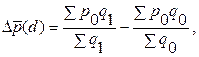
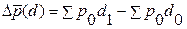
Общий прирост результативного показателя должен быть равен сумме приростов за счет каждого из факторов. Аддитивное разложение имеет вид:
.
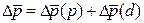
Пример 2: Имеются следующие данные о продаже картофеля на рынках города:
Данные о продаже картофеля на рынках города
| Рынок | Базисный период | Отчетный период | |
| Цена за 1 кг, руб. | Продано, ц | Цена за 1 кг, руб. | Продано, ц |
Определить индекс цен переменного состава, индекс цен фиксированного состава и индекс цен структурных сдвигов. Сделать выводы по результатам расчетов.
1) Индекс цен переменного состава:
, таким образом, в отчетном периоде по сравнению с базисным средняя цена картофеля по рынкам города увеличилась на 15,8 %;
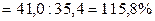
2) Индекс цен фиксированного состава:
– за счет изменения цен на картофель на отдельных рынках средняя цена в отчетном периоде по сравнению с базисным увеличилась на 16,8 %;
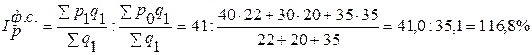
3) Индекс цен структурных сдвигов:
, то есть за счет изменения долей отдельных рынков в их общем объеме продаж (или за счет структурных сдвигов) в отчетном периоде по сравнению с базисным средняя цена картофеля снизилась на 0,8%.
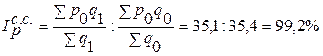
Пример 3: Продукт А производится на двух предприятиях региона:
Данные о себестоимости и физическом объеме выпуска продукта А предприятиями региона
| № предприятия | Себестоимость за единицу продукта, долл. США | Физический объем выпуска, тыс. шт. | |
Базисный период 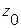 | Отчетный период 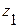 | Базисный период 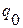 | Отчетный период  |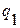
1) изменение средней себестоимости продукта А в процентах и в абсолютном размере;
2) абсолютное изменение средней себестоимости за счет действия отдельных факторов:
а) изменения себестоимости по отдельным предприятиям;
б) структурных сдвигов в общем объеме выпуска продукции.
1) Определим удельные веса каждого предприятия в производстве продукта А в отчетном и базисном периодах:
| № предприятия | Физический объем выпуска, тыс. шт. | Удельный вес выпуска, % | |
| Базисный период 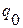| Отчетный период 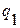| Базисный период 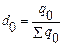 | Отчетный период  |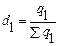
| 0,308 0,692 | 0,452 0,548 | ||
| Итого | 1,000 | 1,000 |
2) Изменение средней себестоимости в процентах характеризует индекс себестоимости переменного состава:
.
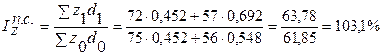
Абсолютное изменение средней себестоимости:
долл. США.
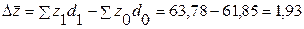
Средняя себестоимость продукта А в отчетном периоде по сравнению с базисным увеличилась на 3,1%, или на 1,93 долл. США;
3) а) Абсолютное изменение средней себестоимости за счет изменения себестоимостей по отдельным предприятиям можно определить, если из числителя индекса фиксированного состава вычесть знаменатель:
долл. США.
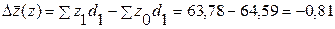
За счет изменения себестоимости продукта А на отдельных предприятиях средняя себестоимость снизилась на 0,81 долл. США;
б) Абсолютное изменение средней себестоимости за счет структурных сдвигов в общем объеме производства можно определить, если из числителя индекса структурных сдвигов вычесть знаменатель:
долл. США.
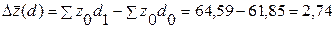
За счет изменения долей отдельных предприятий в производстве продукта А (или за счет структурных сдвигов общем объеме выпуска) его средняя себестоимость увеличилась на 2,74 долл. США.
;
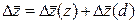
Разновидностью относительных величин является территориальный индекс, т. е. сравнение показателей, относящихся к разным территориям.
Пример: Товарооборот регионов А и В, база сравнения регион В.
, 
, тогда 
.
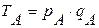
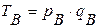
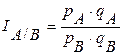
Источник
