Функция общего вида что это значит

Содержание

Чётные и нечётные функции
1. Определение
2. Исследование функции на чётность
3. График чётной и нечётной функции
4. Дополнение. Задачи с параметром
Глава 39. Понятие функции. Основные свойства функций

Чётные и нечётные функции

11 декабря 2021

Сегодня мы разберём:

Определение чётных и нечётных функций
Как проверить, является функция чётной или нечётной
Как выглядят графики чётных и нечётных функций
Дополнение. Задачи с параметром

1. Определение

Определение 1. Функция $f\left( x \right)$, определённая на множестве $M$, называется чётной, если:

$M$ — симметричное относительно нуля множество.
$f\left( -x \right)=f\left( x \right)$.

Определение 2. Функция $f\left( x \right)$, определённая на множестве $M$, называется нечётной, если:

$M$ — симметричное относительно нуля множество.
$f\left( -x \right)=-f\left( x \right)$.

Определение 3. Во всех остальные случаях, когда функция $f\left( x \right)$ не является ни чётной,
ни нечётной, её называют функцией общего вида.

Примеры чётных функций:

Квадратичная: $f\left( x \right)=<^<2>>$; любая степенная функция с чётным показателем: $<^<4>>$, $<^<8>>,$ да хоть $<^<128>>$.
Модуль: $f\left( x \right)=\left| x \right|$. С модулем будет отдельный разговор — он обращает любую функцию в чётную.

Примеры нечётных функций:

Любая степенная функция с нечётным показателем: $f\left( x \right)=<^<3>>$, $<^<5>>$, $<^<2n+1>>$.
Корень третьей степени: $f\left( x \right)=\sqrt[3]$.
Обратная пропорциональность: $f\left( x \right)=<1>/\;$.

2. Исследование функции на чётность

Чтобы узнать, является функция чётной или нечётной (или вообще общего вида), нужны две проверки:

Область определения. Если она не симметрична относительно нуля, то функция общего вида. Если симметрична — переходим ко второй проверке.
Зная $f\left( x \right)$, считаем $f\left( -x \right)$ и $-f\left( x \right)$. Если $f\left( -x \right)=-f\left( x \right)$, то функция нечётная. А если $f\left( -x \right)=f\left( x \right)$, то функция чётная.

Главное, чтобы функция была задана формулой, а не таблицей, графиком или ещё как. Тогда исследование на чётность занимает несколько секунд. Мы сейчас убедимся в этом, но сначала важное замечание.

Что значит «симметричное относительно нуля множество»? Это значит, что если $x\in M$, то и $-x\in M$. Малейшее нарушение этого правила — хотя бы в одной точке — и множество уже не симметрично.

Примеры симметричных множеств:

Примеры несимметричных множеств:

Первые два множества несимметричны всего в одной точке (кстати, какой?). Но этого достаточно, чтобы прекратить исследование и отнести функцию к общему виду.

Разберём несколько примеров. Для начала — стандартный:

Исследуйте на чётность / нечётность функцию

Эта функция определена для всех действительных чисел: $x\in \mathbb$. Это симметричное относительно нуля множество. Пока всё хорошо.

Считаем $f\left( -x \right)$ и $-f\left( x \right)$:

Получили, что $f\left( -x \right)=-f\left( x \right)$. Значит, функция нечётная.

А вот более хитрый случай:

Исследуйте на чётность / нечётность функцию

Область определения. Перед нами рациональная дробь. Её знаменатель должен быть отличен от нуля:

\[\begin 4-x & \ne 0 \\ x & \ne 4 \\ \end\]

Следовательно, область определения

\[M=\left( -\infty ;4 \right)\bigcup \left( 4;+\infty \right)\]

Это множество несимметрично, поскольку $x=-4$ принадлежит этому множеству, а $x=4$ не принадлежит. Всё: функция $f\left( x \right)$ — общего вида.

Дальше попробуйте сами:

Исследуйте на чётность / нечётность функцию

Ответ: $f\left( x \right)$ — общего вида; $g\left( x \right)$ — чётная; $k\left( x \right)$ — нечётная.

Умение быстро определять чётность — чрезвычайно полезный навык. Особенно когда вы начнёте решать задачи с параметрами и всевозможные варианты ДВИ.

3. График чётной и нечётной функции

Всего два факта, которые нужно знать:

Теорема 1. График чётной функции $y=f\left( x \right)$ симметричен относительно оси $OY$.

Теорема 2. График нечётной функции $y=f\left( x \right)$ симметричен относительно начала координат.

Чтобы построить график чётной функции, достаточно построить его правую часть (для $x\ge 0$), а затем симметрично отразить относительно оси $OY$.

С нечётной функцией, на первый взгляд, всё то же самое. Сначала вновь строим правую часть графика (для $x\ge 0$), а затем отражаем её относительно начала координат. Однако практика показывает, что центральная симметрия даётся начинающим ученикам чуть сложнее, чем осевая.

Ниже приведены графики нескольких чётных функций. Попробуйте построить их самостоятельно.

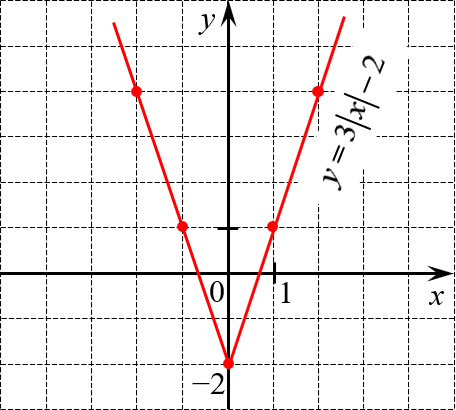
\[y=3\left| x \right|-2\]

Функция чётная. Пусть $x\ge 0$. Тогда функция примет вид

Это линейная функция. Её график — прямая. С учётом отражения относительно оси $OY$ получим:

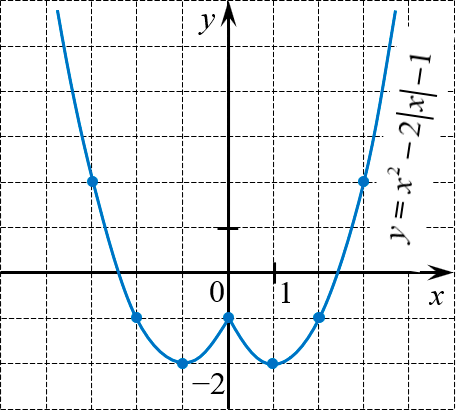
Постройте график функции

Функция чётная. При $x\ge 0$ видим привычную квадратичную функцию

Её график — парабола с вершиной $<_<0>>=<-b>/<2a>\;=<2>/<2>\;=1$. После отражения получим

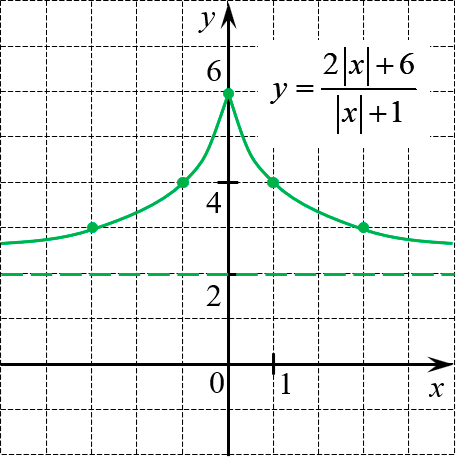
Постройте график функции

Функция чётная. При $x\ge 0$ получим привычную рациональную дробь. Выделим целую часть:

Это обычная гипербола, сдвинутая на 1 влево и на 2 вверх. Итого получим:

Обратите внимание на последний график. При всяком сдвиге и симметрии желательно показывать не только новое положение самого графика, но и положение всех ориентиров: вспомогательная система координат, вертикальные и горизонтальные асимптоты (особенно актуально для гипербол) и т.д.

Зачем всё это нужно? Исследование функции на чётность и нечётность незаменимо для решения сложных уравнений и задач с параметром:

Графический метод решения задач с параметром;
Метод мажорант;
Вместе с периодичностью используется в тригонометрии.

4. Дополнение. Задачи с параметром

Чётность функций редко встречается сама по себе. Прежде всего это инструмент для решения сложных задач.

Известно, что $f\left( x \right)=<^<8>>+a<^<4>>+1$ и $f\left( 2 \right)=353$. Найдите $f\left( -2 \right)$ и значение параметра $a$.

Решение. Очевидно, что функция $f\left( x \right)$ чётная:

Следовательно можем найти $f\left( -2 \right)$:

\[f\left( -2 \right)=f\left( 2 \right)=353\]

Кроме того, подставим $x=2$ и $f\left( 2 \right)=353$ в формулу, задающую функцию:

Задача решена. Ответы:

И ещё одна задача. Попробуйте решить её самостоятельно:

Известно, что $f\left( x \right)=\frac<6075><<^<5>>+k<^<3>>>$ и $f\left( 3 \right)=15$. Найдите $f\left( -3 \right)$ и значение параметра $k$.

Решение. Функция чётная при любом $k\in \mathbb$ (докажите это!), поэтому

\[f\left( -3 \right)=-f\left( 3 \right)=-15\]

Поскольку $f\left( 3 \right)=15$, имеем:

А чтобы действительно разобраться с чётностью, обязательно изучите ещё две темы:

Сдвиги графиков вдоль осей;
Графики функций с модулем.

После этого половина задач с параметром перестанет казаться вам сложными.:)

Источник

Глава 39. Понятие функции. Основные свойства функций

Постоянной величиной называется величина, сохраняющая одно и тоже значение.

Например, отношение длины окружности к ее диаметру есть постоянная величина, равная p.

Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется Параметром.

Переменной называется величина, которая может принимать различные числовые значения.

Например, при равномерном движении S = vt, где путь S и время t – переменные величины, а v – параметр.

Если каждому элементу 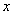множества ( ) ставится в соответствие вполне определенный элемент множества ( ), то говорят, что на множестве задана Функция .

При этом 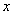называется Независимой переменной (или аргументом), –зависимой переменной, А буква обозначает закон соответствия.

Множество Называется Областью определения (или Существования) функции, а множество – Областью значений функции. Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т. е. множество таких значений , при которых функция вообще имеет смысл.

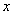
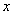
Например, область определения функции есть полуинтервал , так как ; если же переменная обозначает, предположим, время, то при естественном дополнительном условии областью определения функции будет отрезок .

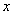
Способы задания функций

Задать функцию – значит Указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие значение функции из области значений функций. Существует три основных способа задания функций: Табличный, аналитический и графический.

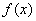
Табличный способ Состоит в том, что функция задается таблицей, содержащей значения аргумента И соответствующие значения функции , например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т. п.

Аналитический способ состоит в задании связи между аргументом и функцией в виде формул. Этот способ наиболее часто встречается на практике. Так, функция , рассматриваемая выше, задана аналитически. Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция

Имеет два аналитических выражения, используемых при различных значениях аргумента.

Графический способ Состоит в том, что соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях и употреблением самопишущих приборов (осциллографы, сейсмографы и т. д.).

Основные свойства функции

1. Четность и нечетность.

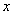
Функция называется Четной, если для любых значений из области определения И Нечетной, Если . В противном случае функция называется функцией Общего вида.

Например, функция является четной, а функция – нечетной. Функция является функцией общего вида, так как и И .

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

Функция называется Возрастающей (Убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть и . Тогда функция возрастает на промежутке X, если и убывает, если .