Фрактально что это значит

Фрактал

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.

Содержание

Термин

Слово «фрактал» может употребляться не только как математический термин. Фракталом в прессе и научно-популярной литературе могут называть фигуры, обладающие какими-либо из перечисленных ниже свойств:

• Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, графикгладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
• Является самоподобной или приближённо самоподобной.
• Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

История

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например,функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Примеры

Самоподобные множества с необычными свойствами в математике

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:

• множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины.
• треугольник Серпинского и ковёр Серпинского — аналоги множества Кантора на плоскости.
• губка Менгера — аналог множества Кантора в трёхмерном пространстве;
• примеры Вейерштрасса и Ван дер Вардена нигде не дифференцируемой непрерывной функции.
• кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины, не имеющая касательной ни в одной точке;
• кривая Пеано — непрерывная кривая, проходящая через все точки квадрата.
• траектория броуновской частицы также с вероятностью 1 нигде не дифференцируема. Её хаусдорфова размерность равна двум.

Рекурсивная процедура получения фрактальных кривых

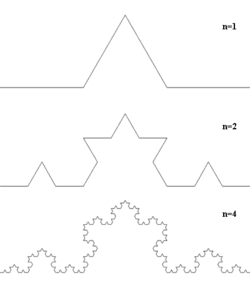
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены четыре первых шага этой процедуры для кривой Коха.

Примерами таких кривых служат:

С помощью похожей процедуры получается дерево Пифагора.

Фракталы как неподвижные точки сжимающих отображений

Свойство самоподобия можно математически строго выразить следующим образом. Пусть — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:

Можно показать, что отображение является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.

Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения — отображения подобия, а — число звеньев генератора.

Для треугольника Серпинского и отображения , , — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении .

В случае, когда отображения — преобразования подобия с коэффициентами 0″ border=»0″/>, размерность фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения . Так, для треугольника Серпинского получаем .

По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения , мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.

Фракталы в комплексной динамике

Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Нас интересует поведение этой последовательности при стремлении n к бесконечности. Эта последовательность может:

• стремиться к бесконечности,
• стремиться к конечному пределу,
• демонстрировать в пределе циклическое поведение, например: z₁, z₂, z₃, z₁, z₂, z₃, …
• вести себя хаотично, то есть не демонстрировать ни один из трёх упомянутых типов поведения.

Множества значений z₀, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.

Так, множество Жюлиа — множество точек бифуркации для многочлена F(z)=z 2 +c (или другой похожей функции), то есть тех значений z₀, для которых поведение последовательности <z_n> может резко меняться при сколь угодно малых изменениях z₀.

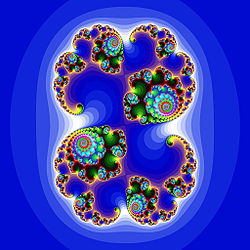
Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z) и рассмотрение множества тех значений параметра, при которых последовательность <z_n> демонстрирует определённое поведение при фиксированном z₀. Так, множество Мандельброта — это множество всех , при которых <z_n> для F(z)=z 2 +c и z₀ не стремится к бесконечности.

Ещё один известный пример такого рода — бассейны Ньютона.

Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления <z_n> к бесконечности (определяемой, скажем, как наименьший номер n, при котором |z_n| превысит фиксированную большую величину A.

Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Стохастические фракталы

Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

• траектория броуновского движения на плоскости и в пространстве;
• граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельброта о том, что её размерность равна 4/3.
• эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например, в модели Изинга и перколяции.
• различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.

В природе

• Бронхиальное дерево
• Сеть кровеносных сосудов
• Деревья
• Молния

Применение

Естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Радиотехника

Фрактальные антенны

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.

Информатика

Сжатие изображений

Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован [источник не указан 779 дней] фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).

Децентрализованные сети

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Экономика и финансы

А. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс.

Источник