Формальная точка зрения что значит

Формальная и диалектическая логика

Основой формальной логики можно считать четыре закона: закон тождества, закон противоречия, закон исключенного третьего и закон достаточного основания.

В основе диалектической логики лежит три закона: закон единства и борьбы противоположностей, закон перехода количества в качество, закон отрицания отрицания.

Основой претензий со стороны формальной логики в сторону диалектической логики можно считать закон противоречия (например, К. Поппер. Что такое диалектика?)

Одним из ответов диалектической логики на это можно считать, что первые три закона формальной логики опираются на закон достаточности основания, а как раз в движении это самое основание изменяется (например, И. Ставинский. Формальная и диалектическая логика как единство противоположностей или развитие классической философии.).

Представим себе металлический шарик диаметром в сантиметр. Шар достаточно идеален, чтобы мы могли рассмотреть какие-то изъяны и неровности. Он одинаков со всех сторон по форме и цвету, как его не крути. Дальше мы сплющиваем шар, положив под пресс, и получаем болванку для монеты. Теперь у нас есть две противоположные стороны. Цвет и материал остались неизменны, но появилось новое свойство, относящееся к форме, – стороны. Дальше мы можем выгравировать изображения на каждой из сторон: орла и решку. Более того, теперь на стороне орла также появилось разделение: область, относящаяся к изображению орла и область вне орла. В итоге последовательными операциями деления мы придали новые свойства изначальному шару. Изначальные свойства, вроде цвета и материала у нас так и остались неизменны, но появились новые: сторона и вне/внутри изображения.

Нетрудно заметить, что в делении шара на орла и решку, обе стороны являются противоположностями друг другу, но в то же время и имеют единство, так как остаются одним и тем же сплюснутым исходным металлическим шариком.

В учебнике логики Челпанова (Г.И. Челпанов. Учебник логики.) есть понятие относительных и абсолютных терминов. «Абсолютный термин – это такой термин, который в своём значении не содержит никакого отношения к чему-либо другому. Относительный термин – это такой термин, который кроме того предмета, который он означает, предполагает существование также и другого предмета.» В учебнике логики Гусева (Д.А. Гусев. Краткий курс логики. Искусство правильного мышления.) такое разделение не упоминается.

Вообще мы не можем определить какой-либо термин, обозначающий некий предмет, не предполагая существования другого предмета, хотя бы существования отрицания исходного предмета. Иначе мы просто не можем никак идентифицировать предмет, нам не с чем сравнить этот предмет и сказать да, это он, или нет, это не он. Получается, что любой термин является относительным. В этом моменте учебник Гусева более корректен, чем учебник Челпанова, однако, простое исключение разделения на абсолютные и относительные термины скрывает суть, а именно отсутствии абсолютных терминов с точки зрения логики.

Когда мы определяем некий новый термин, мы тем самым определяем, как минимум, еще один термин, являющийся отрицанием первого. Даже несмотря на то, что явно мы противоположный термин можем и не описывать, он всё равно существует.

Теперь стоит привести другой пример, связанный с математикой. Встретились Петя, Вася и Лена. У Пети большое спелое красное яблоко, у Васи маленькое зеленое яблоко, а у Лены нет яблок. Петя и Вася отдали свои яблоки Лене, та их взяла, но потом поняла, что не хочет кушать и отдала по яблоку Пете и Васе. Описывая данный пример на языке математики, мы получим со стороны Лены:

1 + 1 + 0 = 2 => 2 – 1 – 1 = 0

Всё вернулось, как и было: у Пети с Васей по яблоку, а у Лены нет яблок. Однако, случилась странная ситуация, как с котом Шредингера. Мы не знаем, какое яблоко кому досталось. С точки зрения математики всё корректно, а вот с точки зрения формальной логики появилась неопределенность. Логическая ошибка, которую мы совершили, заключается в том, что перейдя от красного и зеленого яблока к числам, мы нарушили закон тождества: «иметь не одно значение, значит не иметь ни одного». В нашем случае, за «1» скрывается и красное яблоко, и зеленое.

В этом примере также стоит обратить внимание на то, что мы задаем термин — число, как количественное свойство предметов. Однако среди чисел присутствует число «0», которое обозначает отсутствие предметов. Получается, что самого предмета нет, а свойство этого предмета – количество есть. Таким образом, число «0» нарушает логический закон противоречия.

Как нетрудно заметить, невозможность в формальной логике определить понятие ноля приводит к невозможности определить полностью независимые (в математике: перпендикулярные или ортогональные) понятия. Другими словами, всегда есть проекция любого понятия на любое понятие или все понятия (объекты) являются взаимосвязанными. Закон перехода количества в качество, по сути, отражает эту взаимосвязь всех понятий друг с другом.

В главе о делении учебника логики Челпанова есть пример с треугольниками: остроугольным, тупоугольным и прямоугольным. Термины «острый» и «тупой» присутствуют и не в математике, например, острый и тупой нож. В обычной жизни «острый» и «тупой» являются противоположными понятиями, и по закону исключенного третьего ничего среднего между ними быть не может. Если изображать деление треугольников кругами Эйлера, то самым наглядным примером будут два круга, касающиеся друг друга в одной точке. Однако эта точка, соответствующая прямоугольному треугольнику будет приводить к нарушению и закона тождества, и закона противоречия, и закона исключенного третьего.

Отсутствие ноля отражает отсутствие полной идентичности нескольких предметов. Можно сказать, что любые предметы имеют ненулевую разницу, что согласуется с законом тождества. Без ноля также невозможно определить ни одно натуральное число (и все другие числа), так как, например, число 2 представляет собой сумма двух единиц, а двух одинаковых единиц не может быть.

Вернемся к нашему примеру с шариком. Когда мы сплюснули шар и получили монету, у нас существует и две стороны: орел и решка, и области внутри и вне орла на одной из сторон. Но также взяв изначально шар, мы уже знали, что он металлический и одноцветный. Эти свойства нашего исходного предмета также обозначаются относительными терминами и предполагают существование альтернатив.

То деление, которое мы начали со сплющивания шара, мы можем продолжать без ограничения. Но нас ничего не ограничивает также применить принцип деления и в обратную сторону. Материал шара предполагает существование других материалов, цвет других цветов, форма шара – других форм.

В итоге никаких границ, т.е. некоторых абсолютных значений или терминов, с точки зрения формальной логики быть не может. К таким границам относятся, в том числе, любые начальные условия или аксиомы. Мы можем определить нечто, опираясь на некоторое основание, но это самое основание будет опираться на предыдущее основание и т.д. без ограничений.

Особенно следует отметить, что среди всех понятий основополагающими являются понятия пространства и времени, которые не могут ничем выделяться с точки зрения принципов формальной логики и также являются взаимозависимыми друг с другом и со всеми остальными понятиями. У пространства и времени также нет ни абсолютных, ни начальных значений.

Наш физический мир по наблюдениям в полной мере согласуется с законами формальной логики, однако наша Вселенная имеет некоторые абсолютные значения свойств. Меж тем ответ на это противоречие прост: наша Вселенная есть то самое промежуточное основание, иными словами, подмножество логической мультивселенной, где существуют все возможные варианты всех понятий. Человеческое сознание и мышление, есть процесс конструирования произвольных ограниченных подмножеств логической мультивселенной через варьирование и различные комбинации понятий.

Математика является формально противоречивой (что для основы математики – арифметики доказал Курт Гёдель еще в 1930 году в «теореме о неполноте»). А натуральные числа ошибочно носят звание «натуральных». Математику можно использовать в локальных задачах, как ограниченную приближенную модель, но при расширении области применения математика рано или поздно натыкается на внутренние логические противоречия.

В силу невозможности внятной экспериментальной проверки в современной физике очень много теорий далеких не только от реальности, но и от логики. В связи с этим естественной реакцией общества уже достаточно давно стала замена изучения логики на математику. Строгие логичные теории стали заменяться принципом практической реализуемости.

Исключение из формальной логики понятия абсолютных терминов снимает её противоречия с диалектической логикой, что сводит их в единое целое, где диалектическая логика дополняет формальную.

Такая единая логика может позволить свести в общую непротиворечивую теорию все наблюдаемые явления в физике за последние сто с лишним лет.

PS: Современная физика и логика

Пример с шариком наглядно демонстрирует суть квантовых эффектов. Пространство-время ошибочно понимается, как некая среда, в которой находится материя. Пространство-время – это абстракция, в том смысле, что оно противоположно материи. Соответственно, пространство-время неразрывно связано с материей – является её обратной стороной. Свойства пространства-времени, в первую очередь размерность, есть отражение свойств материи.

Идеальный шар является таким объектом, что его описание одинаково, независимо от размерности пространства: отрезок в одномерном пространстве, круг в двухмерном пространстве, шар в трехмерном, и т.д. Более того, по наблюдению свойств шара нельзя никак понять, если не знать заранее, эту самую размерность пространства. Когда же из шарика мы делаем монету, то свойство размерности уже идентифицируется по наблюдению самой монеты.

Именно в этом заключается суть квантовых эффектов, которые наблюдаются у обособленных частиц, но полностью исчезают, как только частицы начинают объединяться. Единичные частицы попросту не имеют пространственных свойств, поэтому при наблюдении происходит считывание свойств частицы преобразованием её свойств к трехмерному классическому пространству наблюдателя. Так, например, появляется электронное облако. Сюда же попадает и корпускулярно-волновой дуализм, когда наблюдаемая частица вроде как «заранее» знает, как мы её будем ловить, и ведет себя соответственно.

Уже давно квантовые эффекты пытаются трактовать через вероятности, дуализмы и прочие идеи, прямо нарушающие законы формальной логики. Позднее придумали бесконечные струны в одиннадцатимерные пространствах, хотя проще и логичнее понять суть, что есть пространство и что, оно не независимо от материи. Хотя, к слову, уже из теории относительности это напрямую следует. Сама же теория относительности занимается искривлением пространства непонятно относительно чего. Находясь внутри пространства невозможно понять, что оно искривлено. По рисунку на листе бумаги (изнутри листа) нельзя понять, насколько согнут лист.

Общеизвестный принцип причинности, т.е. взаимозависимость всех понятий, т.е. отсутствие ортогональных понятий (равно как и отсутствие параллельных понятий) наглядно демонстрирует история трех великих геометрий. У Евклида через точку, вне прямой можно провести одну прямую параллельную данной, у Лобачевского две прямых, а у Римана ни одной прямой. В этом плане геометрия Римана, где любые прямые где-то пересекаются, как раз отражает физическую реальность, т.е. тот самый принцип причинности. В физике такая взаимосвязь, например, выражается в законе сохранения энергии.

Источник

Значение словосочетания «формальные признаки»

Значение слова «формальный&raquo

ФОРМА́ЛЬНЫЙ , —ая, —ое; —лен, —льна, —льно. 1. только полн. ф. Официальный, законный, произведенный по форме (в 7 знач.). Формальные доказательства (установленные заранее законом). Формальное обвинение. (Малый академический словарь, МАС)

Значение слова «признак&raquo

ПРИ́ЗНАК , -а, м. Показатель, примета, знак, по которым можно узнать, определить что-л. Признаки отравления. Признаки болезни. (Малый академический словарь, МАС)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова суконка (существительное):

Ассоциации к слову «формальный&raquo

Ассоциации к слову «признак&raquo

Синонимы к словосочетанию «формальные признаки&raquo

Предложения со словосочетанием «формальные признаки&raquo

• Анализируя древнеацтекский пантеон по чисто формальным признакам, нужно отметить существование двух божественных фратрий на основе такого признака, как пол.

Цитаты из русской классики со словосочетанием «формальные признаки»

• Для определения Духа Св. нет никаких внешних формальных признаков .

Сочетаемость слова «формальный&raquo

Сочетаемость слова «признак&raquo

Понятия, связанные со словосочетанием «формальные признаки»

Афоризмы русских писателей со словом «признак&raquo

• Любовь бывает разная и у всех по-разному, но ее неотъемлемый признак — именно категоричность. И самая категоричная — первая любовь.

Отправить комментарий

Дополнительно

Значение слова «формальный&raquo

ФОРМА́ЛЬНЫЙ , —ая, —ое; —лен, —льна, —льно. 1. только полн. ф. Официальный, законный, произведенный по форме (в 7 знач.). Формальные доказательства (установленные заранее законом). Формальное обвинение.

Значение слова «признак&raquo

ПРИ́ЗНАК , -а, м. Показатель, примета, знак, по которым можно узнать, определить что-л. Признаки отравления. Признаки болезни.

Предложения со словосочетанием «формальные признаки&raquo

Анализируя древнеацтекский пантеон по чисто формальным признакам, нужно отметить существование двух божественных фратрий на основе такого признака, как пол.

А если критериев эффективности нет, то параноидальный контроль по формальным признакам может привести к потере самых ценных кадров.

Если некий рассказ по формальным признакам можно отнести в разные пограничные группы, то последнее слово остаётся за автором.

Источник

Чем интуитивная логика отличается от формальной и как правильно делать умозаключения из утверждений «все мужики козлы» и «некоторые бабы дуры»

У каждого человека есть набор логических правил, с помощью которых он рассуждает, — интуитивная логика. Несмотря на то что мы все ею постоянно пользуемся, у нее есть недостатки. А когда нас захлестывают эмоции, мы вообще забываем о всякой логике — это касается таких важных для нас областей, как здоровье, отношения, психология или питание. На примерах из этих областей знакомимся с формальной логикой: она поможет нам найти правильные ответы и не допустить ошибки даже в тех ситуациях, когда эмоции пытаются взять верх.

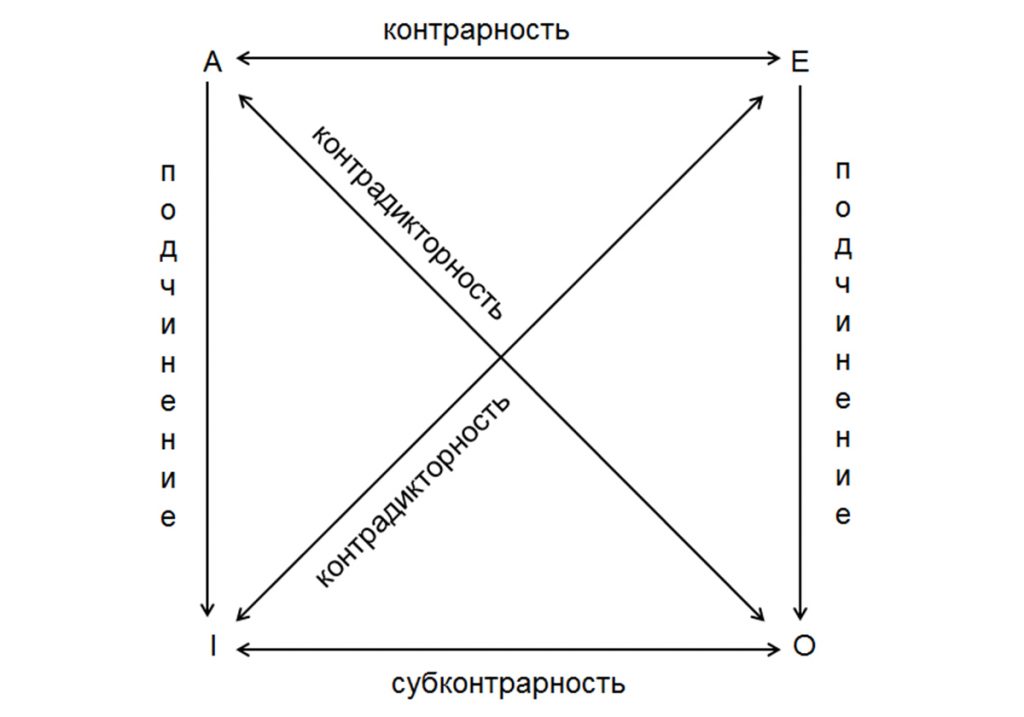
Почему логика — квадратная

Логика называется формальной потому, что работает с формой, а не содержанием, то есть с тем, как устроены предложения и как они между собой связаны. Это полезно тем, что мы можем отстраниться от смысла предложений, которые могут задевать наши чувства, и сделать правильное умозаключение без эмоционального влияния.

Давайте начнем с простых умозаключений, которые принято называть «умозаключениями по логическому квадрату» .

Логика (на нашем начальном уровне) имеет дело с утвердительным предложениями — простыми суждениями, которые по двум признакам делятся на четыре группы.

1-й признак: количество

По количеству суждения делятся на общие и частные .

«Некоторые бабы дуры» — частное суждение.

2-й признак: качество

По качеству бывают утвердительные и отрицательные суждения.

«Мой муж козел» — утвердительное суждение.

«Моя жена не дура» — отрицательное суждение.

Если мы объединим эти два признака, то получим четыре типа суждений, а в скобках укажем их классические обозначения:

«Ни одна панацея не работает» — общеотрицательные (E).

«Некоторые методы доказательной медицины работают» — частноутвердительные (I).

«Некоторые методы народной медицины не работают» — частноотрицательные (O).

Запомнить символьное обозначение классов суждений легко, если знать их происхождение от латинских слов “affirno” — утверждать и “nego” — отрицать, из которых были взяты гласные: первые — для общих суждений, вторые — для частных.

Вы уже догадались, что углы квадрата — четыре типа суждений. Часто его рисуют вот так:

Зачем нам нужен этот квадрат? Очень просто: он показывает, в каких отношениях находятся суждения разных классов. То есть с его помощью мы можем проверять себя, правильно ли мы делаем преобразования суждений, и выяснять, куда именно закралась ошибка.

Все или некоторые? Делаем правильные выводы

Обычно мы делаем логические преобразования со сложными для анализа суждениями. Но мы рассмотрим силу логического квадрата на примере содержательно простых суждений.

Предположим, что мы думаем так:

Какие выводы мы можем из этого сделать? Это общеутвердительное (А) суждение, следовательно, мы можем сказать, что:

— это тоже верное суждение, так как оно частноутвердительное (I) и (смотрим на квадрат) находится в отношении подчинения с A. Все отрицательные суждения при этом будут ложными, неправильными, так как они будут контрарными (общеотрицательные E) и контрадикторными (частноотрицательные O) по отношению к изначальному суждению (общеутвердительные A). То есть неправильно будет сказать «некоторые мужики — не козлы».

Несколько интереснее получается, если у нас исходное суждение частноутвердительное :

Можно ли из этого сделать вывод, что все бабы дуры? Нет, из частного нельзя вывести общее, только наоборот: отношение подчинения в квадрате — одностороннее! Вот так-то.

А что с отрицательными суждениями?

Можно ли сделать вывод, что если некоторые бабы дуры, то среди баб встречаются умные? То есть верно ли частноотрицательное суждение, если верно частноутвердительное?

Казалось бы, это так и просится: если только часть грибов съедобные, то ясно же, что есть какие-то несъедобные грибы. Или если некоторые лебеди белые, то часто кажется, что предполагается наличие каких-то других лебедей.

Однако с точки зрения формальной логики это не так! Отношение субконтрарности означает, что суждения не могут быть одновременно ложными — и только. То есть не может быть такого, что неверны оба утверждения: и «некоторые бабы дуры», и «некоторые бабы не дуры». Такого не может быть, а вот другие сочетания возможны: мы говорим, что некоторые бабы дуры, а это может означать, что на самом деле все они дуры, просто мы этого не знаем или нам сейчас это неважно. А может быть, что действительно есть не дуры. Надо наблюдать — но это уже не про логику, а про жизнь.

Никто или некоторые?

Вот, например, исходное общеотрицательное суждение, которое можно сделать из отрицания знаменитого мифа о том, что люди используют свой мозг только на 10 %.

Оно дает нам на самом деле довольно мало информации. Мы можем вывести из него «некоторые не используют мозг на 10 %». По-русски эту звучит весьма неоднозначно — и это еще одна проблема использования естественного языка в формальной логике, но об этом в другой раз.

Возьмем за изначальное суждение частноотрицательное:

Какой вывод из этого можно сделать? Некоторые делают вывод, что врачи травят людей таблетками и нужно лечиться чем-то «натуральным». На самом деле можно сделать лишь один вывод: общеутвердительное суждение «все таблетки лечат» не является истинным — что никогда не вызывало сомнений, особенно учитывая, что медикаменты довольно часто употребляют без рекомендации врачей.

Для закрепления расшифруем связи в квадрате, которые еще не называли, и перейдем к рассмотрению некоторых типичных ошибок, связанных с умозаключениями по логическому квадрату:

Контрарность — суждения в этом отношении могут быть одновременно ложными либо одно из них истинное, другое ложное, одновременно истинными быть не могут.

Субконтрарность — суждения могут быть одновременно истинными либо одно из двух истинное, оба ложными не могут быть.

Контрадикторность — одно из двух суждений обязательно истинное.

Мне помогло — и вам поможет, или Поспешное обобщение

Очень часто можно встретить примерно такие высказывания:

«Мне чай из иван-чая помог, советую вам пить каждый день иван-чай — тоже всё будет просто отлично!»

Что не так с этим умозаключением?

Мы не будем разбирать фактическую ошибку (иван-чай, тем более высушенный и заваренный, имеет мало чего полезного) или часто упоминающуюся ошибку «„после“ — не значит „вследствие“», а поговорим исключительно об ошибке, связанной с логическим квадратом.

Для этого нам из исходных предложений нужно получить формально-логические суждения.

«Некоторым (мне, моим детям, мужу) помог иван-чай».

Почему мы делаем первое суждение частноутвердительным, а второе — общеутвердительным? В первом случае речь идет об одном или нескольких людях, которым помог иван-чай, то есть не о целом классе предметов, не о всём множестве, не обо всех людях. Во втором же случае речь идет о случайном представителе людей, потому это можно принять за целое множество людей, которые имеют то же заболевание, что и тот, кому помогло, или вообще всех людей, если речь идет о панацее или повышении, стимуляции иммунитета, например. В некоторых случаях говорят именно так: мне помогло — значит, и всем поможет. Так мы и делаем общеутвердительное суждение.

Уже на этом этапе видна проблема обсуждаемого умозаключения: от частноутвердительного суждения происходит переход к общеутвердительному, что не соответствует их отношению подчинения.

Такая ошибка называется поспешное обобщение — весьма распространенная ошибка, особенность которой в том, что она не всегда приводит к ложным результатам, потому людям иногда кажется, что так можно делать.

Все бабы дуры, я одна королева!

Думаю, вы встречали подобные высказывания:

«Никто не умеет ездить, я один король дороги!»

Это класс довольно часто встречающихся высказываний. Давайте разберемся, в чем они ошибочны.

Основная ошибка связана с тем, что люди исключают себя из множества: да, я нарушаю правила дорожного движения, но я же не такой, как все остальные.

Людям не хочется причислять себя группам людей — хотя у них в действительности нет оснований для исключения из них. Основную роль в этом необоснованном исключении играют эмоции, связанные с чем-то неприятным.

Красивый и развернутый пример такого процесса самисключиения мы можем найти, например, у Льва Николаевича Толстого в повести «Смерть Ивана Ильича»:

«В глубине души Иван Ильич знал, что он умирает, но он не только не привык к этому, но просто не понимал, никак не мог понять этого.

Тот пример силлогизма, которому он учился в логике Кизеветера: Кай — человек, люди смертны, потому Кай смертен, казался ему во всю его жизнь правильным только по отношению к Каю, но никак не к нему. То был Кай-человек, вообще человек, и это было совершенно справедливо; но он был не Кай и не вообще человек, а он всегда был совсем, совсем особенное от всех других существо; он был Ваня с мама, папа, с Митей и Володей, с игрушками, кучером, с няней, потом с Катенькой, со всеми радостями, горестями, восторгами детства, юности, молодости. Разве для Кая был тот запах кожаного полосками мячика, который так любил Ваня! Разве Кай целовал так руку матери и разве для Кая так шуршал шелк складок платья матери? Разве он бунтовал за пирожки в Правоведении? Разве Кай так был влюблен? Разве Кай так мог вести заседание?

И Кай точно смертен, и ему правильно умирать, но мне, Ване, Ивану Ильичу, со всеми моими чувствами, мыслями, — мне это другое дело. И не может быть, чтобы мне следовало умирать. Это было бы слишком ужасно».

Замечали за собой похожие рассуждения?

«Какая вредная еда. Все, кто её едят, толстеют. Но со мной — совсем другая история!»

Как все подобные мысли связаны с формальной логикой? Если переводить эти рассуждения в необходимую для нас форму, то получится, что в них человек пытается одновременно считать истинными суждения двух типов:

A — общеутвердительное («Все мужчины — агенты патриархата»)

и O — частноотрицательное («Некоторые (я) не агенты патриархата, а профеминисты»).

Могут ли они быть одновременно истинными?

Нет, не могут, так как находятся в отношении контрадикторности: это противоречащие друг другу суждения, которые не могут быть одновременно истинными.

Мы говорили, что при контрадикторности только одно суждение может быть истинным, более того, должно быть истинным. Сами посудите: если все лебеди белые, то некоторые из них не могут быть черными, а если всё же нашли в Австралии черных лебедей, то уже не все лебеди будут белыми.

Можно попробовать обосновать утверждение, что я действительно не такой/такая, как другие, потому что на меня не действуют общие правила («Все мужчины, воспитанные в патриархате, — угнетатели, а я — мужчина, воспитанный феминисткой»).

С одной стороны, это уже не логический аспект, а фактологический, с другой — зачастую совершенно несложно, если избавиться от эмоций, разобраться с тем, что вы не выделяетесь в отдельный класс. Вот если бы вы были единственным чернокожим в толпе белых — тогда было бы хоть какое-то основание для выделения вас в отдельную группу, да и то современные исследования показывают, что основное различие между расами — именно что цветовое.

Эмоции — один из главных врагов логического мышления, именно они очень часто мешают нам принимать взвешенные логические решения.

Мы это видели и в первой разобранной ошибке, и особенно во второй. Будет эта же проблема и в третьей ошибке.

Иногда не иногда!

— Дорогой, ты иногда поступаешь так умно!
— Ага, значит, иногда я поступаю так глупо, да?

Думаю, что вы сталкивались с чем-то подобным в своей жизни, причем тут не важен пол: такой ответ можно услышать и от девушки, и от парня, но правильный ли сделан вывод?

Для того чтобы сказать однозначно, так, чтобы результат был общий для всех подобных ситуаций, чтобы не нужно было каждый раз подбирать фактические аргументы, что бывает сложно, мы приведем рассуждения в безэмоциональный формальный вид. Сделать это не так просто, и в процессе преобразования у нас получится довольно сильно отличающиеся по форме предложения:

— Дорогой, некоторые твои поступки умны.
— Ага, следовательно, некоторые мои поступки не являются умными.

Надеюсь, вы уже натренировали свой глаз и легко поняли, какого типа эти суждения: они оба частные, но первое утвердительное, а второе отрицательное. Тут есть некоторая тонкость при анализе: можно исходное суждение видоизменить так, что получится частноутвердительное суждение:

«Ага, следовательно, некоторые мои поступки являются не умными».

Для работы по логическому квадрату нам важно, чтобы у двух сравниваемых суждений были бы одинаковые части. Так, в первом суждении у нас в отношении находятся «твои поступки» и «умны», потому во втором должны быть они же, а не «твои поступки» и «не умны». Может меняться связка с «являются» на «не являются» — это показывает смену типа суждения, но не меняет содержания, сути. Именно поэтому нам нужно получить суждение: «Некоторые мои поступки не являются умными».

Что же мы можем сказать про эти суждения?

Если мы вспомним логический квадрат, то выясним, что частные суждения находятся в отношении субконтрарности, то есть могут быть одновременно истинными, но не могут быть одновременно ложными. При этом нужно помнить, что может так быть, что только одно из этих двух суждений истинное. Это приводит к тому, что если мы имеем одно истинное частное суждение — утвердительное, как в нашем примере, — то мы не можем однозначно сказать, является ли субконтрарное — частноотрицательное суждение — истинным или ложным.

«Некоторые автомобили загрязняют атмосферу».

Можем ли мы из этого сделать вывод, что некоторые автомобили не загрязняют?

«Некоторые гомеопатические препараты не содержат активного компонента».

Можно ли из этого сделать вывод, что в некоторых гомеопатических препаратах всё-таки есть действующее вещество? (Спойлер: нет, не должно быть, иначе они не гомеопатические).

Вот пример риторического приема, когда вы говорите оппоненту:

Это может быть воспринято им (или теми, кто наблюдает за вашим спором) эмоционально: как будто в других местах беседы он был неправ и только тут вы готовы с ним, так уж и быть, согласиться. С точки зрения логики, как мы обсуждали выше, тут нет ни ошибки, ни указания на то, что оппонент был неправ в остальных местах. Что вы ему и объясните, когда он возмутится и выразит несогласие, показав себя не с лучшей стороны.

Так иногда можно использовать ошибки, которые люди допускают в формальной логике из-за эмоций, себе на пользу.

Как видите, найти логически правильный ответ достаточно легко, даже если не знаешь точного логического объяснения. Но когда в дело вмешиваются эмоции, то дойти до правильного вывода — даже зная формальную логику — не так-то просто.

Знание описанных выше простых правил позволяет четко и просто выявить логические пробелы в собственных и чужих умозаключениях и спокойно, аргументированно указать на них.

Источник