- Президентский ФМЛ №239
- Инструменты пользователя
- Инструменты сайта
- Содержание
- Отношение площадей треугольников с равными элементами
- Теорема
- Докажем первый пункт теоремы.
- Докажем второй пункт теоремы.
- Докажем третий пункт теоремы.
- Свойство биссектрисы треугольника
- Доказательство
- Если высоты двух треугольников равны то их площади относятся как основания что это значит
- Урок геометрии по теме «Решение задач с использованием свойств площадей». 8-й класс
- Отношение площадей треугольников, имеющих общую высоту (основание)
Президентский ФМЛ №239
Инструменты пользователя
Инструменты сайта
Содержание
Отношение площадей треугольников с равными элементами
Теорема
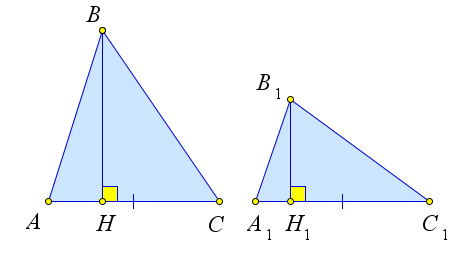
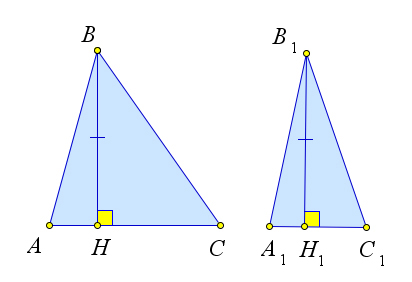
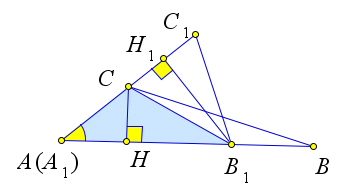
Докажем первый пункт теоремы.
Рассмотрим треугольники $\triangle ABC$ и $\triangle A_1B_1C_1$ в которых высоты $BH$ и $B_1H_1$ равны.
Докажем второй пункт теоремы.
Рассмотрим треугольники $\triangle ABC$ и $\triangle A_1B_1C_1$ в которых основания $AC$ и $A_1C_1$ равны.
Докажем третий пункт теоремы.
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ в которых углы $A$ и $A_1$ равны.
Докажем, что их площади относятся как произведения сторон, заключающих эти углы.
Наложим треугольник $A_1B_1C_1$ на треугольник $ABC$ так, чтобы вершина $A_1$ совместилась с вершиной $A$, а стороны $A_1B_1$ и $A_1C_1$ наложились соответственно на лучи $AB$ и $AC$.
Треугольники $ABC$ и $AB_1C$ имеют общую высоту $CH$, поэтому $\dfrac
Треугольники $AB_1C$ и $AB_1C_1$ имеют общую высоту $B_1H_1$, поэтому $\dfrac
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим его сторонам.
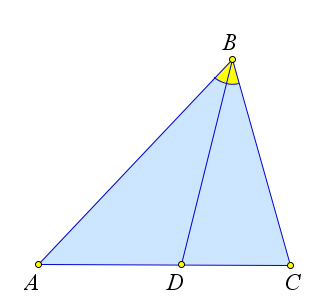
Доказательство
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $BD$.
Действительно, так как у треугольников $ABD$ и $BDC$ высота, проведенная из вершины $B$, общая, то $S_
Кроме того у этих треугольников есть равные углы, следовательно их площади относятся, как произведения сторон: $S_
Сравнивая полученные равенства для отношения площадей, получаем: $\dfrac
Источник
Если высоты двух треугольников равны то их площади относятся как основания что это значит
В элементарной математике, самыми трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.
Предлагаем один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.
Основные свойства площадей.
Свойство №1
Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

Свойство №2

Рассмотрим отношение площадей этих треугольников $$\frac
Упростив, получим $$\frac
| Свойство №3 Если два треугольника имеют общий |  |  | Доказательство: Рассмотрим ▲ABC и ▲MBN . Пусть AB = k MB, BC = k NB и $$\angle ABC = \angle MBN$$. Используя формулу площади треугольника вида $$S = \frac<1> <2>\cdot a \cdot b \cdot sin\gamma$$ , рассмотрим отношение подобных площадей ▲ABC и ▲MBN . Тогда $$\frac |
Медиана треугольника делит его на две равновеликие части.

Свойство №6
Медианы треугольника делят его на три равновеликие части.

Средние линии треугольника площади S отсекают от него треугольники площади .

ІV. Дополнительное задание.
В оставшееся время работаем по карточкам.
Задание карточки: Проведите все высоты треугольника. Отметьте их h1, h2, h3. (Задаются различные виды треугольников: остроугольные, прямоугольные, тупоугольные)
1. С11(2), вар.4. из [2] решить тремя способами. Это задание разбирается по готовому чертежу устно одним из способов, увиденным учащимися.
Условие задачи: “В ромбе ABCD диагонали равны 5 см и 12 см. На диагонали АС взята точка М так, что АМ : МС = 4 : 1. Найдите площадь треугольника AMD”.
2. Дополнительная задача: “Докажите, что медианы треугольника делят его на три равновеликих треугольника”.
Использованная литература:
- Геометрия: Учебник для 7 – 9 кл. общеобразовательных учреждений/Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др., М: Просвещение, 2006;
- Дидактические материалы по геометрии для 8 класса/Б. Г. Зив, В. М. Мейлер, М: Просвещение, 2005.
Источник
Отношение площадей треугольников, имеющих общую высоту (основание)
Разделы: Математика
Цели урока:
- Сформировать умение использовать формулу площади треугольника при решении задач;
- Рассмотреть ключевые задачи об отношении площадей треугольников, имеющих общую высоту (основание). Познакомить учащихся с методами решения задач по теме.
Оборудование урока:
- Компьютер.
- Мультимедийный проектор.
- Экран.
Раздаточный материал.
- карточки с вопросами для опроса по домашнему заданию;
- презентация к уроку (Приложение 1);
- карточки для выполнения самостоятельной работы.
Этапы урока
- Организационный момент.
- Проверка домашнего задания (усвоение материала предыдущего урока)
- Закрепление ранее изученного материала
- Самостоятельная работа обучающего характера
- Постановка домашнего задания.
- Подведение итогов урока.
Ход урока
1. Организационный момент
Сообщаем тему урока. Поясняем важность рассматриваемого на уроке материала, говорим о том, что сведения последних уроков по площадям имеют широкое применение, сегодня на уроке используем их при решении задач.
Для эффективности работы в начале проверим домашнее задание и повторим изученный теоретический материал.
2. Проверка домашнего задания
Опрос учащихся у доски:
- доказательство теоремы о площади ?.
- доказательство следствий из неё
- решение номеров домашнего задания.
В это время с классом работаем устно, по слайдам заранее подготовленной презентации.
3) Если AM=MC, то сравните площади этих треугольников.
Записать вывод в тетрадь:
Медиана делит треугольник на два равновеликих (равных по площади) треугольника, и площадь каждого из которых равна половине площади данного треугольника.
ВМ – медиана 
ВК – медиана 
Найдите отношение площадей
5) Известно, что SABС=20см 2 (по условию предыдущего задания)
Чему равно отношение площадей двух треугольников, имеющих общее основание?
Записываем вывод в тетради:
Площади треугольников, имеющих общее основание, относятся как высоты, проведенные к основанию.
Далее заслушиваем и обсуждаем теоретические ответы учащихся по ДЗ.
3. Закрепление ранее изученного материала.
1. Выполняем задание №40 стр. 18-19 рабочей тетради по геометрии для 8 кл.
На рисунке точка М делит сторону АС 
Площадь 
2. Решаем задачу №475 учебника.
Начертите 
Обсуждаем решение, используя слайды презентации
4. н/о (если позволяет время)
Данный параллелограмм разделите на три равновеликие части прямыми, выходящими из одной вершины.
Аналогично, ВВ2 делит 
4. Самостоятельная работа обучающего характера
Вариант -1
1) СК – медиана 
SСКВ = 32 см 2 . Найти SABС
2) SКDM = 40 см 2
На стороне КМ отмечена точка А так, что КА : АМ = 2 :3
Вариант — 2
1) АМ – медиана 
Найти площадь 
2) SDРК = 60 см 2
На стороне DК отмечена точка А так, что DА : АK = 3 :1
5. Постановка домашнего задания
Д.З. по учебнику стр. 124-125 № 473; 506; 511(а)
6. Подведение итогов урока
Литература
1. Геометрия 7-9. / Л.С. Атанасян, В.Ф. Бутузов и др./ “ Просвещение”, ОАО “Московский учебник”,М., 2008;
2. Рабочая тетрадь для 8 кл. об/об учреждений. Геометрия. / Атанасян Л.С. и др. / “Просвещение”, М, 2005;
2. Полонский В.Б., Рабинович Е.М., Якир М.С. / Геометрия: Задачник к школьному курсу М.: АСТ-ПРЕСС: Магистр-S, 1998.
Источник

 .
.  .
.


 , то
, то 

 .
.






