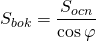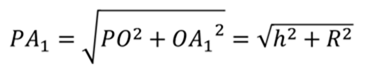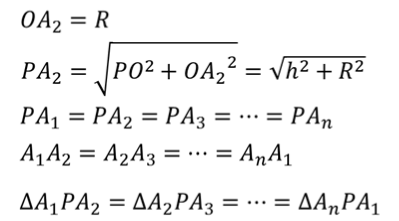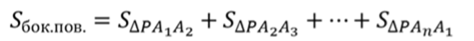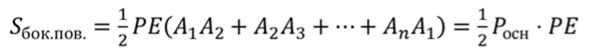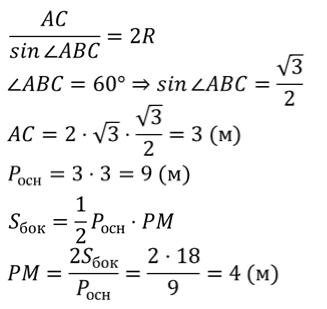Если пирамида правильная что это значит

Что такое правильная пирамида: определение, виды, свойства

В данной публикации мы рассмотрим определение, виды (треугольная, четырехугольная, шестиугольная) и основные свойства правильной пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение правильной пирамиды

Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

Самые распространенные разновидности правильных пирамид: треугольная, четырехугольная и шестиугольная. Рассмотрим их подробнее.

Виды правильной пирамиды

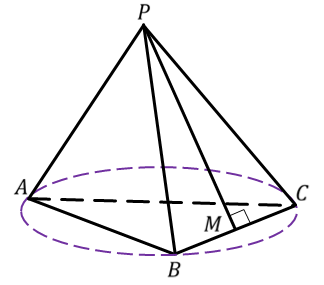
Правильная треугольная пирамида

• Основание – правильный/равносторонний треугольник ABC.
• Боковые грани – одинаковые равнобедренные треугольники: ADC, BDC и ADB.

Примечание: если у правильной треугольной пирамиды все ребра равны, она также называется правильным тетраэдром.

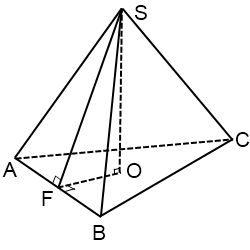
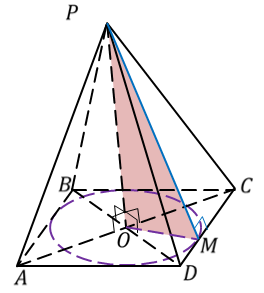
Правильная четырехугольная пирамида

• Основание – правильный четырехугольник ABCD, другими словами, квадрат.
• Боковые грани – равные равнобедренные треугольники: AEB, BEC, CED и AED.
• Проекция вершины E на основание – точка O, является точкой пересечения диагоналей квадрата ABCD.
• EO – высота фигуры.
• EN и EM – апофемы (всего их 4, на рисунке в качестве примера изображено только два).

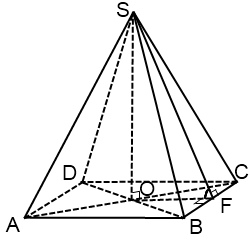
Правильная шестиугольная пирамида

• Основание – правильный шестиугольник ABCDEF.
• Боковые грани – равные равнобедренные треугольники: AGB, BGC, CGD, DGE, EGF и FGA.
• Проекция вершины G на основание – точка O, является точкой пересечения диагоналей/биссектрис шестиугольника ABCDEF.
• GO – высота пирамиды.
• GN – апофема (всего их должно быть шесть).

Свойства правильной пирамиды

1. Все боковые ребра фигуры равны. Другими словами вершина пирамиды находится на одинаковом расстоянии от всех углов ее основания.
2. Угол между всеми боковыми ребрами и основанием одинаковый.
3. Все грани наклонены к основанию под одним и тем же углом.
4. Площади всех боковых граней равны.
5. Все апофемы равны.
6. Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения перпендикуляров, проведенных к серединам боковых ребер.

Примечание: Формулы для нахождения площади поверхности, а также объема пирамиды представлены в отдельных публикациях.

Источник

Геометрические фигуры. Правильная пирамида.

Правильная пирамида — когда основанием пирамиды является правильный многоугольник, а высота проецируется в центр основания (или проходит через него).

В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.

Правильная пирамида обладает следующими свойствами:

• боковые рёбра правильной пирамиды имеют равную величину;
• в правильной пирамиде каждая боковая грань — конгруэнтный равнобедренный треугольник;
• во все правильные пирамиды можно как вписать, так и описать вокруг неё сферу;
• когда центры вписанной и описанной сферы совпадают, значит, сумма плоских углов у вершины пирамиды равняется , а всякий из них соответственно , где n — число сторон многоугольника основания;
• площадь боковой поверхности правильной пирамиды равняется ½ произведения периметра основания на апофему.

Формулы для правильной пирамиды.

V — объем пирамиды,

S — площадь основания пирамиды,

h — высота пирамиды,

Sb — площадь боковой поверхности пирамиды,

a — апофема (не путать с α) пирамиды,

P — периметр основания пирамиды,

n — число сторон основания пирамиды,

b — длина бокового ребра пирамиды,

α — плоский угол при вершине пирамиды.

Ниже указанная формула определения объема используется лишь для правильной пирамиды:

V — объем правильной пирамиды,

h — высота правильной пирамиды,

n — количество сторон правильного многоугольника, основания правильной пирамиды,

a — длина стороны правильного многоугольника.

Боковое ребро правильной пирамиды находят по формуле:

где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),

n — количество сторон правильного многоугольника (основание правильной пирамиды),

a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) — основания правильной пирамиды,

h — высота правильной пирамиды (OS).

Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.

Нужно разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.

Правильная треугольная пирамида.

Правильная треугольная пирамида — это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.

Формулы для правильной треугольной пирамиды.

Формула для нахождения объема правильной треугольной пирамиды:

V — объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,

h — высота правильной пирамиды,

a — длина стороны основания правильной пирамиды.

Так как правильная треугольная пирамида — это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.

Еще одним частным случаем правильно пирамиды является тетраэдр.

Источник

Узнать ещё

Знание — сила. Познавательная информация

Правильная пирамида

Среди задач на пирамиду правильная пирамида встречается чаще других. Чтобы легко решать такие задачи, нужно знать свойства правильной пирамиды.

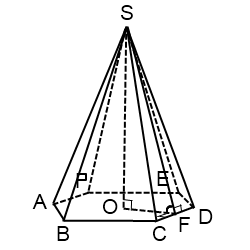
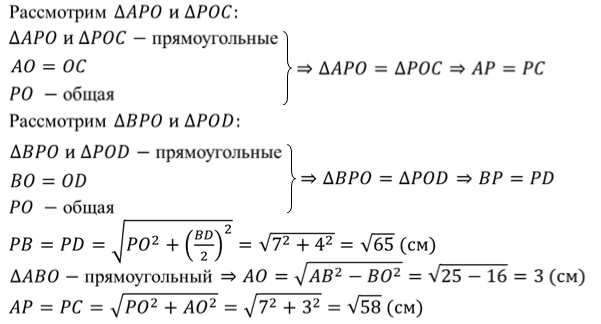
Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.

Высота боковой грани, проведенная из вершины правильной пирамиды, называется апофемой.

— двугранный угол при основании пирамиды

SO — высота пирамиды

Свойства правильной пирамиды

— боковые ребра равны;

— боковые грани равны (все — равнобедренные треугольники);

— двугранные углы при основании равны;

— боковые ребра одинаково наклонены к плоскости основания;

— основание высоты пирамиды является центром вписанной и описанной около основания окружностей;

— каждая точка высоты правильной пирамиды равноудалена от вершин основания;

— каждая точка высоты правильной пирамиды равноудалена от боковых граней;

— высота правильной пирамиды образует с апофемами равные углы.

Боковая поверхность правильной пирамиды

В правильной пирамиде основание является ортогональной проекцией боковой поверхности. Поэтому

где φ — двугранный угол при основании. Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле

Еще одна формула боковой поверхности правильной пирамиды:

где P — периметр основания, l — апофема пирамиды.

Источник

Пирамида. Правильная пирамида

Урок 27. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Пирамида. Правильная пирамида»

С пирамидой мы с вами знакомились в курсе геометрии базовой школы. Давайте вспомним, какой многогранник мы назвали пирамидой и основные элементы пирамиды.

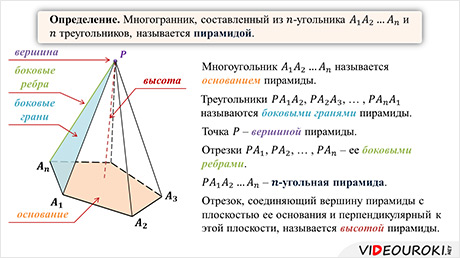
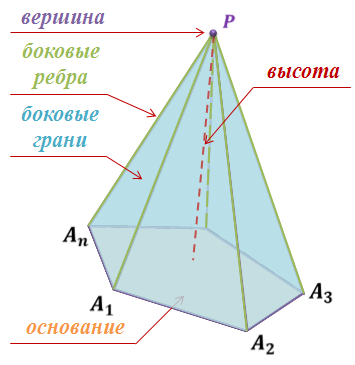
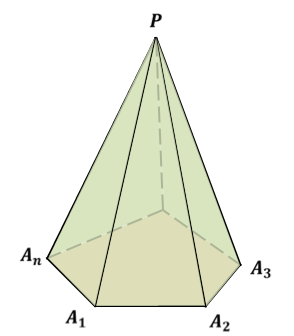
Итак, рассмотрим многоугольник A₁A₂…A_n и точку P, не лежащую в плоскости этого многоугольника. Соединим точку ПЭ отрезками с вершинами многоугольника. В итоге получим n треугольников: PA₁A₂, PA₂A₃, …, PA_nA₁. Многогранник, составленный из n-угольника A₁A₂…A_n и этих n треугольников, называется пирамидой.

Многоугольник A₁A₂…A_n называется основанием пирамиды. Треугольники PA₁A₂, PA₂A₃, …, PA_nA₁ называются боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA₁, PA₂,…, PA_n – ее боковыми ребрами.

Пирамиду с вершиной P и основанием A₁A₂…A_n называют n-угольной пирамидой и обозначают так: PA₁A₂…A_n.

Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

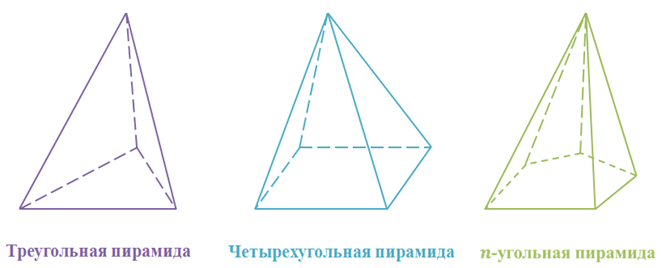
Пирамида в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то пирамида называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.

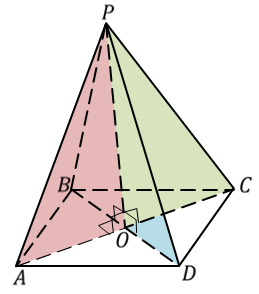
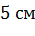
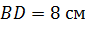
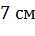
Задача. Основанием пирамиды является ромб, сторона которого равна , а одна из диагоналей равна . Найти длину боковых ребер пирамиды, если высота пирамиды проходит через точку пересечения диагоналей основания и равна .

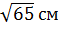
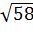
Ответ. , см.

Давайте дадим определение правильной пирамиды.

Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

На сегодняшнем уроке мы подробно рассмотрим правильные пирамиды.

Сейчас давайте попробуем доказать одно из свойств правильной пирамиды. А именно докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

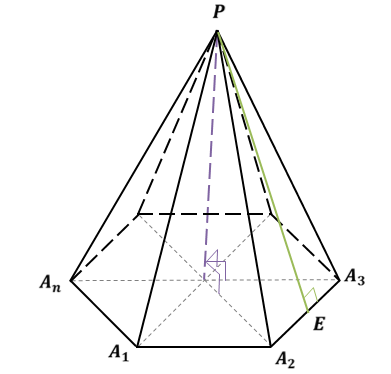
Рассмотрим правильную пирамиду PA₁A₂…A_n. Сначала докажем, что все боковые ребра этой пирамиды равны. Проведем высоту пирамиды.

Поскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA₁, то OP равно h, OA₁ равно R.

Таким образом, мы доказали, что боковые ребра правильной пирамиды равны. А значит, боковые грани правильной пирамиды – это равнобедренные треугольники. Поскольку в основании лежит правильный многоугольник, значит, основания боковых граней равны между собой. То есть боковые грани равны между собой по трем сторонам.

Что и требовалось доказать.

Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Запишем формулу для вычисления площади боковой поверхности правильной пирамиды.

Мы уже доказали, что боковые грани правильной пирамиды – равные равнобедренные треугольники. Высоты этих треугольников равны апофеме пирамиды. Тогда площадь боковой грани находится по формуле .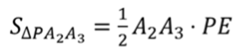

Подставим эти площади в формулу площади боковой поверхности. Вынесем половину апофемы за скобки, тогда в скобках получим периметр основания.

Что и требовалось доказать.

Решим несколько задач.

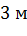
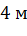
Задача. Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен , высота пирамиды равна . Найти площадь боковой поверхности пирамиды.

Решим еще одну задачу.

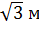
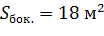
Задача. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен . . Найти длину апофемы.

Подведем итоги урока.

Сегодня на уроке мы вспомнили, какая фигура называется пирамидой. Какие пирамиды называются правильными. Познакомились со свойствами правильных пирамид. Решили несколько задач.

Источник