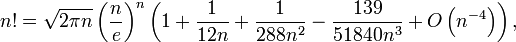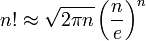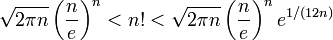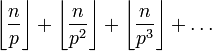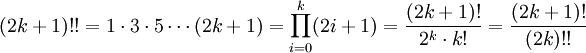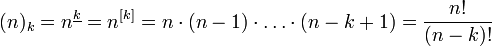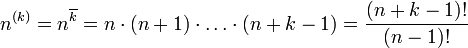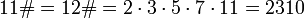Двойной факториал что это значит

Двойной факториал

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

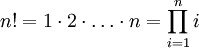
По определению полагают 0! = 1 . Факториал определён только для целых неотрицательных чисел.

Иногда словом «факториал» неформально называют восклицательный знак.

Содержание

Свойства

Комбинаторное определение

В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества <A,B,C,D> можно линейно упорядочить 4!=24 способами:

Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .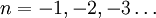

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые в степени

,

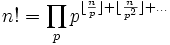
где произведение берется по всем простым числам.

Другие свойства

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

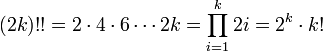
По определению полагают 0!! = 1 .

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал дает число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Примориал (англ. Primorial ) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов начинается так:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

Суперфакториалы

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

Последовательность суперфакториалов начинается (с n = 0 ) с

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial ), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0 ) равны:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал n — произведение первых n (m − 1) -уровневых факториалов, то есть

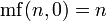
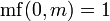
где для n > 0 и .

Субфакториал

Субфакториал 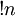определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

Ссылки

См. также

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Двойной факториал» в других словарях:

Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия

Двойной крестик — Одинарный и двойной крестики разными шрифтами Типографский крестик (†, в Юникоде U+2020, в dagger;), иногда его называют «кинжалом», «обелиском», «даггером», типографический знак. Двойной крестик (‡, в Юникоде U+2021, в Dagger;) вариант «кинжала… … Википедия

Праймориал — Факториал числа n (обозначается n!, произносится эн факториал) произведение всех натуральных чисел до n включительно: . По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Эта функция часто используется в… … Википедия

Примориал — Факториал числа n (обозначается n!, произносится эн факториал) произведение всех натуральных чисел до n включительно: . По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Эта функция часто используется в… … Википедия

Восклицательный знак — ! Именно так должен выглядеть этот символ Юникод U+00 … Википедия

Список интегралов от экспоненциальных функций — Ниже приведён список интегралов (первообразных функций) от экспоненциальной функции. Для более полного списка интегралов смотрите таблицу интегралов и другие списки интегралов. Заметим, что везде опущена аддитивная константа интегрирования. для … Википедия

Гиперсфера — Стереографическая проекция поверхности 3 сферы на трёхмерное пространство. На рисунке изображены три координатных направления на 3 сфере: параллели (красный), меридианы (синий) и гипермеридианы (зелёный). В исход … Википедия

Эллиптический интеграл — В интегральном исчислении, эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно и Леонардом Эйлером. В современном представлении, эллиптический интеграл это некоторая… … Википедия

Tcl — Запрос «TCL» перенаправляется сюда; о минидистрибутиве Linux см. Tiny Core Linux. Tcl Семантика: императивный … Википедия

TCL — Семантика: императивный, скриптовый Тип исполнения: интерпретатор Появился в: 1988 г. Автор(ы): Джон Остераут Последняя версия: 8.5.7 / 15 апреля 2009 … Википедия

Источник

В математике есть 9 (. ) факториалов. Все они — в этой статье

Приветствую Вас, уважаемые Читатели! Итак, сегодня хочу рассказать об удивительном математическом зоопарке факториалов. Оказывается, кроме привычной для всех операции, есть еще целых 8 вариантов. Поехали!

1. Факториал

Возникает естественным образом в комбинаторике — науке, в которой изучаются задачи, связанные с выбором и расположением различных элементов чаще всего конечных множеств. Подробнее о его происхождении здесь.

2. Двойной факториал

Этот факториал имеет просто громадное количество приложений в комбинаторике и достоин отдельного материала. Впервые он использовался при выводе замечательного произведения Уоллиса , связывающего натуральные числа и число π:

3. Субфакториал

Этот представитель семейства в отличие от обычного факториала, который определяет количество перестановок, определяет количество беспорядков. Подробнее — в моём недавнем материале.

Дальше — математическая экзотика

4. Праймориал

Определяется как произведение простых чисел, меньших или равных данному. Подробная информация и особенности его применения — здесь .

5. Суперфакториал Слоуна

Название дано создателем уникальной в своём роде Онлайн Энциклопедии Целочисленных Последовательностей (OEIS) . Определяется как произведение факториалов чисел, меньших или равных заданному.

6. Суперфакториал Пиковера

Удивительно быстрорастущая функция. Для числа 3 — это уже вот такая невообразимая башня:

7. Экспоненциальный факториал

По сравнению с предыдущим представителем растет «медленно». Например, для выражения выше — это 262144. Правда, для числа 6 в результате уже 10^183230 нулей.

8. Гиперфакториал

Растет еще медленнее, чем предшествующие два. Только лишь на 14 шаге число нулей приближается к гуголу .

9. Фиббоначиал (бонус)

Равняется произведению первых n чисел Фибоначчи.

P.S. Кроме перечисленных существуют еще возрастающие и убывающие факториалы, но они являются частным случаем факториала обычного.

А еще есть факториал дробного числа! Читайте о нём в моём увлекательном материале! Еще можете заглянуть сюда и узнать, что такое числа-факторионы , и почему их всего 4 !

Спасибо за внимание! Статьте «Нравится» этому материалу и подписывайтесь на канал!

• TELEGRAMиFacebook— там я публикую не только интересные статьи, но иматематический юмор и многое другое.

Источник

В школе такому не учат. Что такое двойной факториал?

Привет, любители математики!

Многие из нас, а я всерьез полагаю, что даже все, знают что такое факториал числа.

Факториал натурального числа n — это произведение всех натуральных чисел от n до 1. Или от 1 до n. Разницы никакой

Этому учат еще в школе и сложного совершенно ничего нет. Но, оказывается, факториалы бывают разные.

В данной статье я хочу вкратце поведать о двойном факториале.

На самом деле, несмотря на свое название, он не удваивает значение, суть его совершенно в другом. Двойным его прозвали, потому что запись двойного факториала выглядит так:

Двойной факториал — это произведение всех натуральных чисел в интервале от 1 до n, имеющих ту же четность, что и n.

Как все это выглядит в живую?

Например, если мы хотим взять двойной факториал 7, то нужно проделать следующие действия:

Ну, а двойной факториал четного, например 6, вычисляют по следующей схеме:

Как видите, все предельно просто. Четное число — перемножаем четные числа, нечетное — нечетные.

Из интересностей, двойной факториал нуля равен:

Хотя, если копать глубже и немного разобраться в комбинаторике, с которой факториалы неразлучные друзья, то окажется, что когда у вас на столе ничего нет и комбинировать то нечем — это единственная возможная комбинация, т.е. факториал нуля — единица. Об этом на моем канале есть целая публикация .

Статья создавалась исключительно в познавательных целях и для обычного пользователя не несет никакой практической пользы! Надеюсь, было просто интересно и познавательно. Расширять кругозоры — дело тоже полезное 🙂

Подписывайтесь на меня в соц сетях. Там, надеюсь, тоже будет много интересного 🙂

Источник

Двойной факториал — Double factorial

В математика, то двойной факториал или же полуфакторный из числа п , обозначаемый п‼ , [1] это продукт всех целые числа от 1 до п которые имеют то же самое паритет (нечетное или четное) как п . [2] То есть,

п ! ! = ∏ k = 0 ⌈ п 2 ⌉ − 1 ( п − 2 k ) = п ( п − 2 ) ( п − 4 ) ⋯ . < displaystyle n !! = prod _ ^ < left lceil < frac <2>> right rceil -1> (n-2k) = n (n-2) (n-4) cdots.>

Даже для п , двойной факториал

п ! ! = ∏ k = 1 п 2 ( 2 k ) = п ( п − 2 ) ( п − 4 ) ⋯ 4 ⋅ 2 , < displaystyle n !! = prod _ ^ < frac <2>> (2k) = n (n-2) (n-4) cdots 4 cdot 2 ,, >

и для нечетных п это

п ! ! = ∏ k = 1 п + 1 2 ( 2 k − 1 ) = п ( п − 2 ) ( п − 4 ) ⋯ 3 ⋅ 1 . < Displaystyle п !! = prod _ ^ < frac <2>> (2k-1) = n (n-2) (n-4) cdots 3 cdot 1 ,.>

Например, 9‼ = 9 × 7 × 5 × 3 × 1 = 945 . Нулевой двойной факториал 0‼ = 1 как пустой продукт. [3] [4]

В последовательность двойных факториалов для четных п = 0, 2, 4, 6, 8. начинается как

1, 2, 8, 48, 384, 3840, 46080, 645120, . (последовательность A000165 в OEIS)

Последовательность двойных факториалов для нечетных п = 1, 3, 5, 7, 9. начинается как

1, 3, 15, 105, 945, 10395, 135135, . (последовательность A001147 в OEIS)

Период, термин нечетный факториал иногда используется для двойного факториала нечетного числа. [5] [6]

Содержание

История и использование

Месерв (1948) [7] (возможно, самая ранняя публикация, использующая двойную факториальную нотацию) [8] утверждает, что двойной факториал был первоначально введен для того, чтобы упростить выражение некоторых тригонометрические интегралы которые возникают при выводе Уоллис продукт. Двойные факториалы также возникают при выражении объема гиперсфера, и у них есть много приложений в перечислительная комбинаторика. [2] [9] Они происходят в Студенты т -распределение (1908), хотя Госсет не использовала нотацию с двойным восклицательным знаком.

Отношение к факториалу

Поскольку двойной факториал включает только половину множителей обычного факториал, его значение не намного больше квадратного корня из факториала п! , и он намного меньше повторного факториала (п!)! .

Факториал ненулевого п может быть записано как произведение двух двойных факториалов: [3]

п ! = п ! ! ⋅ ( п − 1 ) ! ! , < Displaystyle п! = п !! cdot (п-1) !! ,,>

п ! ! = п ! ( п − 1 ) ! ! = ( п + 1 ) ! ( п + 1 ) ! ! , < displaystyle n !! = < frac <(n-1) !!>> = < frac <(n + 1)!><(n + 1) !!>> ,,>

где знаменатель отменяет нежелательные множители в числителе. (Последняя форма также применяется, когда п = 0 .)

Для четного неотрицательного целого числа п = 2k с k ≥ 0 , двойной факториал может быть выражен как

п ! ! = 2 k k ! . < Displaystyle п !! = 2 ^ к! ,.>

Для нечетных п = 2k − 1 с k ≥ 1 , объединение двух представленных выше дисплеев дает

п ! ! = ( 2 k ) ! 2 k k ! = ( 2 k − 1 ) ! 2 k − 1 ( k − 1 ) ! . < displaystyle n !! = < frac <(2k)!> <2 ^ k!>> = < frac <(2k-1)!> <2 ^ (k-1 )!>> ,.>

Для нечетного положительного целого числа п = 2k − 1 с k ≥ 1 , двойной факториал может быть выражен через k -перестановки 2k в качестве [2] [8]

( 2 k − 1 ) ! ! = 2 k п k 2 k = ( 2 k ) k _ 2 k . < displaystyle (2k-1) !! = < frac <_ <2k>P_ > <2 ^ >> = < frac <(2k) ^ < underline >> < 2 ^ >> ,.>

Приложения в перечислительной комбинаторике

Двойные факториалы мотивированы тем фактом, что они часто встречаются в перечислительная комбинаторика и другие настройки. Например, п‼ для нечетных значений п считает

• Идеальное соответствие из полный графикK_{п + 1} для нечетных п . В таком графе любая единственная вершина v имеет п возможен выбор вершины, с которой он может быть сопоставлен, и после того, как этот выбор сделан, остается проблема выбора идеального сопоставления в полном графе с двумя меньшими вершинами. Например, полный граф с четырьмя вершинами а, б, c, и d имеет три идеальных соответствия: ab и CD, ac и bd, и объявление и до н.э. [2] Идеальное соответствие можно описать несколькими другими эквивалентными способами, включая инволюции без неподвижных точек на множестве п + 1 Предметы (перестановки в котором каждый цикл — пара) [2] или хордовые диаграммы (наборы аккордов набора п + 1 точки, равномерно расположенные на окружности, так что каждая точка является концом ровно одной хорды, также называемой Брауэр диаграммы). [9][10][11] Количество совпадений в полных графах, без ограничения совпадений, чтобы быть идеальным, вместо этого задается телефонные номера, которое может быть выражено как суммирование двойных факториалов. [12]
• Перестановки Стирлинга, перестановки мультимножество чисел 1, 1, 2, 2, . k , k в котором каждая пара равных чисел разделена только большими числами, где k = п + 1 / 2 . Две копии k должны быть смежными; удаление их из перестановки оставляет перестановку, в которой максимальный элемент k − 1 , с п позиции, в которые соседняя пара k значения могут быть размещены. Из этой рекурсивной конструкции по индукции следует доказательство того, что перестановки Стирлинга подсчитываются двойными перестановками. [2] В качестве альтернативы, вместо ограничения на то, что значения между парой могут быть больше, чем она, можно также рассмотреть перестановки этого мультимножества, в которых первые копии каждой пары появляются в отсортированном порядке; такая перестановка определяет соответствие на 2k позиции перестановки, так что снова количество перестановок может быть подсчитано с помощью двойных перестановок. [9]
• Упорядоченные в куче деревья, деревья с k + 1 узлы помечены 0, 1, 2, . k , так что корень дерева имеет метку 0, каждый другой узел имеет метку большего размера, чем его родительский, и так, что дочерние элементы каждого узла имеют фиксированный порядок. An Эйлер тур дерева (с удвоенными ребрами) дает перестановку Стирлинга, и каждая перестановка Стирлинга представляет дерево таким образом. [2][13]
• Бинарные деревья без корней с п + 5 / 2 маркированные листья. Каждое такое дерево может быть образовано из дерева, у которого на один лист меньше, путем подразделения одного из п ребра дерева и сделав новую вершину родительской для нового листа.
• Бинарные деревья с корнями с п + 3 / 2 маркированные листья. Этот случай аналогичен случаю без корней, но количество ребер, которые могут быть подразделены, является четным, и в дополнение к подразделению ребра можно добавить узел к дереву с одним меньшим листом, добавив новый корень, два дочерних элемента которого меньшее дерево и новый лист. [2][9]

Каллан (2009) и Дейл и Луна (1993) перечислить несколько дополнительных объектов с таким же последовательность подсчета, в том числе «трапециевидные слова» (цифры в смешанный корень система с увеличивающимися нечетными основаниями), с меткой высоты Дайковые тропы, упорядоченные деревья с пометкой высоты, «нависающие пути» и определенные векторы, описывающие листового потомка с наименьшим номером каждого узла в корневом двоичном дереве. За биективные доказательства что некоторые из этих объектов равны, см. Руби (2008) и Марш и Мартин (2011). [14] [15]

Четные двойные факториалы дают номера элементов гипероктаэдрические группы (знаковые перестановки или симметрии гиперкуб)

Расширения

Отрицательные аргументы

Обычный факториал, расширенный до гамма-функция, имеет столб для каждого отрицательного целого числа, предотвращая определение факториала для этих чисел. Однако двойной факториал нечетных чисел может быть расширен до любого отрицательного нечетного целочисленного аргумента, инвертируя его отношение повторения

п ! ! = п × ( п − 2 ) ! ! < Displaystyle п !! = п раз (п-2) !!>

п ! ! = ( п + 2 ) ! ! п + 2 . < Displaystyle п !! = < гидроразрыва <(п + 2) !!><п + 2>> ,.>

Используя эту обратную рекуррентность, (−1)‼ = 1, (−3)‼ = −1 и (−5)‼ = 1 / 3 ; отрицательные нечетные числа с большей величиной имеют дробные двойные факториалы. [2] В частности, это дает, когда п нечетное число,

( − п ) ! ! × п ! ! = ( − 1 ) п − 1 2 × п . < displaystyle (-n) !! times n !! = (- 1) ^ < frac <2>> times n ,.>

Сложные аргументы

Игнорируя приведенное выше определение п‼ для четных значений п , двойной факториал для нечетных целых чисел может быть расширен до большинства действительных и комплексных чисел z отмечая, что когда z является положительным нечетным целым числом, то [16] [17]

z ! ! = z ( z − 2 ) ⋯ 3 ⋅ 1 = 2 z − 1 2 ( z 2 ) ( z − 2 2 ) ⋯ ( 3 2 ) = 2 z − 1 2 Γ ( z 2 + 1 ) Γ ( 1 2 + 1 ) = 2 z + 1 π Γ ( z 2 + 1 ) = ( z 2 ) ! 2 z + 1 π . < displaystyle < begin z !! & = z (z-2) cdots 3 cdot 1 & = 2 ^ < frac <2>> left ( < frac <2>> right) left ( < frac <2>> right) cdots left ( < frac <3><2>> right) & = 2 ^ < frac <2>> < frac < Gamma left (< frac <2>> + 1 right)> < Gamma left (< frac <1 ><2>> + 1 right)>> & = < sqrt < frac <2 ^ > < pi>>> Gamma left ( < frac <2 >> + 1 right) = left ( < frac <2>> right)! < Sqrt < frac <2 ^ > < pi>>> ,. конец <выровнен>>>

Отсюда можно вывести альтернативное определение z‼ для неотрицательных четных целых значений z :

( 2 k ) ! ! = 2 π ∏ я = 1 k ( 2 я ) = 2 k k ! 2 π , < displaystyle (2k) !! = < sqrt < frac <2>< pi>>> prod _ ^ (2i) = 2 ^ k! < sqrt < frac <2>< pi>>> ,,>

со значением 0‼ в этом случае

0 ! ! = 2 π ≈ 0.797 884 5608 … . < displaystyle 0 !! = < sqrt < frac <2>< pi>>> приблизительно 0,797 , 884 , 5608 dots ,.>

Найденное выражение для z‼ определен для всех комплексных чисел, кроме отрицательных четных целых чисел. Используя его как определение, объем из п -размерный гиперсфера радиуса р можно выразить как [18]

V п = 2 ( 2 π ) п − 1 2 п ! ! р п . < displaystyle V_ = < frac <2 (2 pi) ^ < frac <2>>> > R ^ ,.>

Дополнительные удостоверения

Для целых значений п ,

∫ 0 π 2 грех п ⁡ Икс d Икс = ∫ 0 π 2 потому что п ⁡ Икс d Икс = ( п − 1 ) ! ! п ! ! × < 1 если п странно π 2 если п даже. < displaystyle int _ <0>^ < frac < pi><2>> sin ^ x , dx = int _ <0>^ < frac < pi><2>> cos ^ x , dx = < frac <(n-1) !!>> times < begin 1 & < text > n < text < нечетно>> < frac < pi><2>> & < text > n < text <четно.>> end >>

Используя вместо этого расширение двойного факториала нечетных чисел до комплексных чисел, формула

∫ 0 π 2 грех п ⁡ Икс d Икс = ∫ 0 π 2 потому что п ⁡ Икс d Икс = ( п − 1 ) ! ! п ! ! π 2 . < displaystyle int _ <0>^ < frac < pi><2>> sin ^ x , dx = int _ <0>^ < frac < pi><2>> cos ^ x , dx = < frac <(n-1) !!>> < sqrt < frac < pi><2>>> ,.>

Двойные факториалы также могут использоваться для вычисления интегралов от более сложных тригонометрических полиномов. [7] [19]

Двойные факториалы нечетных чисел связаны с гамма-функция по личности:

( 2 п − 1 ) ! ! = 2 п ⋅ Γ ( 1 2 + п ) π = ( − 2 ) п ⋅ π Γ ( 1 2 − п ) . < displaystyle (2n-1) !! = 2 ^ cdot < frac < Gamma left (< frac <1><2>> + n right)> < sqrt < pi>>> = (- 2) ^ cdot < frac < sqrt < pi>> < Gamma left (< frac <1><2>> — n right)>> ,. >

Некоторые дополнительные тождества, включающие двойные факториалы нечетных чисел: [2]

( 2 п − 1 ) ! ! = ∑ k = 1 п − 1 ( п k + 1 ) ( 2 k − 1 ) ! ! ( 2 п − 2 k − 3 ) ! ! , ( 2 п − 1 ) ! ! = ∑ k = 0 п ( 2 п − k − 1 k − 1 ) ( 2 k − 1 ) ( 2 п − k + 1 ) k + 1 ( 2 п − 2 k − 3 ) ! ! , ( 2 п − 1 ) ! ! = ∑ k = 1 п ( п − 1 ) ! ( k − 1 ) ! k ( 2 k − 3 ) ! ! . < displaystyle < begin (2n-1) !! & = sum _ ^ < binom > (2k-1)! ! (2n-2k-3) !! ,, (2n-1) !! & = sum _ ^ < binom <2n-k-1>> < frac <(2k-1) (2n-k + 1)>> (2n-2k-3) !! ,, (2n-1) !! & = sum _ ^ < frac <(n-1)!><(k-1)!>> k (2k-3) !! ,. end <выровнено>>>

Приближение для отношения двойного факториала двух последовательных целых чисел:

( 2 п ) ! ! ( 2 п − 1 ) ! ! ≈ π п . < displaystyle < frac <(2n) !!><(2n-1) !!>> приблизительно < sqrt < pi n>>.>

Это приближение становится более точным, поскольку п увеличивается.

Обобщения

Определения

Точно так же, как двойной факториал обобщает понятие единственный факториал, следующее определение целочисленных множественных факториальных функций (многофакторность), или же α -факториальные функции, расширяет понятие двойной факториальной функции для α ∈ ℤ + :

0\,;\\1&<\text< if >>-\alpha п ! ( α ) = < п ⋅ ( п − α ) ! ( α ) если п >0 ; 1 если − α п ≤ 0 ; 0 иначе. < displaystyle n! _ <( alpha)>= < begin n cdot (n- alpha)! _ <( alpha)>& < text > n> 0 ,; 1 & < text > — alpha 0 ,; 1 & < text > — alpha

Альтернативное расширение многофакторной

В качестве альтернативы многофакторный п!_(α) может быть расширен до большинства действительных и комплексных чисел п отмечая, что когда п на единицу больше, чем положительное кратное α тогда

п ! ( α ) = п ( п − α ) ⋯ ( α + 1 ) = α п − 1 α ( п α ) ( п − α α ) ⋯ ( α + 1 α ) = α п − 1 α Γ ( п α + 1 ) Γ ( 1 α + 1 ) . < Displaystyle < begin n! _ <( alpha)>& = n (n- alpha) cdots ( alpha +1) & = alpha ^ < frac < alpha>> left ( < frac < alpha>> right) left ( < frac < alpha>> right) cdots left ( < frac < alpha +1>< alpha>> right) & = alpha ^ < frac < alpha>> < frac < Gamma left (< frac < alpha>> + 1 right)> < Gamma left (< frac <1>< alpha>> + 1 right)>> ,. end <выравнивается>>>

Это последнее выражение имеет гораздо более широкое определение, чем исходное. Таким же образом п! не определен для отрицательных целых чисел, и п‼ не определен для отрицательных целых чисел, п!_(α) не определен для отрицательных кратных α . Однако он определен для всех других комплексных чисел. Это определение согласуется с более ранним определением только для тех целых чисел п удовлетворение п ≡ 1 мод α .

В дополнение к расширению п!_(α) к самым сложным числам п , это определение работает для всех положительных действительных значений α . Кроме того, когда α = 1 , это определение математически эквивалентно Π (п) функция, описанная выше. Кроме того, когда α = 2 , это определение математически эквивалентно альтернативное расширение двойного факториала.

Обобщенные числа Стирлинга, расширяющие многофакторные функции

Класс обобщенных Числа Стирлинга первого рода определяется для α > 0 следующим треугольным рекуррентным соотношением:

[ п k ] α = ( α п + 1 − 2 α ) [ п − 1 k ] α + [ п − 1 k − 1 ] α + δ п , 0 δ k , 0 . < displaystyle left [< begin n k end > right] _ < alpha>= ( alpha n + 1-2 alpha) left [ < begin > n-1 k end > right] _ < alpha>+ left [ < begin n-1 k-1 end > right] _ < alpha>+ delta _ delta _ ,.>

Эти обобщенные α -факторные коэффициенты затем сгенерируйте различные символические полиномиальные произведения, определяющие множественный факториал, или α -факторные функции, (Икс − 1)!_(α) , так как

( Икс − 1 | α ) п _ := ∏ я = 0 п − 1 ( Икс − 1 − я α ) = ( Икс − 1 ) ( Икс − 1 − α ) ⋯ ( Икс − 1 − ( п − 1 ) α ) = ∑ k = 0 п [ п k ] ( − α ) п − k ( Икс − 1 ) k = ∑ k = 1 п [ п k ] α ( − 1 ) п − k Икс k − 1 . < displaystyle < begin (x-1 | alpha) ^ < underline > &: = prod _ ^ left (x-1-i alpha right) = (x-1) (x-1- alpha) cdots < bigl (>x-1- (n-1) alpha < bigr)>& = sum _ < k = 0>^ left [ < begin n k end > right] (- alpha) ^ (x-1) ^ & = sum _ ^ left [ < begin n k end > right] _ < alpha>(- 1) ^ x ^ ,. end <выровнено>>>

Различные полиномиальные разложения в предыдущих уравнениях фактически определяют α -факторные произведения для нескольких различных случаев наименьших остатков Икс ≡ п₀ мод α за п₀ ∈ <0, 1, 2, . α − 1> .

Обобщенный α -факторные полиномы, σ (α)
п (Икс) куда σ (1)
п (Икс) ≡ σ_п(Икс) , которые обобщают Полиномы свертки Стирлинга от однофакторного случая к многофакторному, определяются как

σ п ( α ) ( Икс ) := [ Икс Икс − п ] ( α ) ( Икс − п − 1 ) ! Икс ! < displaystyle sigma _ ^ <( alpha)>(x): = left [ < begin x xn end > right] _ <( alpha)> < frac <(xn-1)!>>>

за 0 ≤ п ≤ Икс . Эти многочлены имеют особенно красивую замкнутую форму обычная производящая функция данный

∑ п ≥ 0 Икс ⋅ σ п ( α ) ( Икс ) z п = е ( 1 − α ) z ( α z е α z е α z − 1 ) Икс . < displaystyle sum _ x cdot sigma _ ^ <( alpha)>(x) z ^ = e ^ <(1- alpha) z>left (< frac < alpha ze ^ < alpha z>> -1>> right) ^ ,.>

Другие комбинаторные свойства и разложения этих обобщенных α -факторные треугольники и полиномиальные последовательности рассматриваются в Шмидт (2010). [20]

Точные конечные суммы с участием нескольких факториальных функций

Предположим, что п ≥ 1 и α ≥ 2 целочисленные. Затем мы можем разложить следующие одиночные конечные суммы, включающие многофакторную, или α -факторные функции, (αn − 1)!_(α) , с точки зрения Символ Поххаммера и обобщенные рациональнозначные биномиальные коэффициенты в качестве

( α п − 1 ) ! ( α ) = ∑ k = 0 п − 1 ( п − 1 k + 1 ) ( − 1 ) k × ( 1 α ) − ( k + 1 ) ( 1 α − п ) k + 1 × ( α ( k + 1 ) − 1 ) ! ( α ) ( α ( п − k − 1 ) − 1 ) ! ( α ) = ∑ k = 0 п − 1 ( п − 1 k + 1 ) ( − 1 ) k × ( 1 α + k − п k + 1 ) ( 1 α − 1 k + 1 ) × ( α ( k + 1 ) − 1 ) ! ( α ) ( α ( п − k − 1 ) − 1 ) ! ( α ) , < displaystyle < begin ( alpha n-1)! _ <( alpha)>& = sum _ ^ < binom > (- 1) ^ times left ( < frac <1>< alpha>> right) _ <- (k + 1)>left ( < frac <1>< alpha>> — n right) _ times < bigl (>alpha (k + 1) -1 < bigr)>! _ <( alpha)> < bigl (>альфа (nk-1) -1 < bigr)>! _ <( alpha)>& = sum _ ^ < binom > (- 1) ^ times < binom << frac <1>< alpha>> + kn> > < binom << frac <1>< alpha >> — 1> > times < bigl (>alpha (k + 1) -1 < bigr)>! _ <( Alpha)> < bigl (>alpha (nk- 1) -1 < bigr)>! _ <( Alpha)>,, end >>

и, кроме того, у нас аналогично есть разложения этих функций в двойную сумму, заданные формулой

( α п − 1 ) ! ( α ) = ∑ k = 0 п − 1 ∑ я = 0 k + 1 ( п − 1 k + 1 ) ( k + 1 я ) ( − 1 ) k α k + 1 − я ( α я − 1 ) ! ( α ) ( α ( п − 1 − k ) − 1 ) ! ( α ) × ( п − 1 − k ) k + 1 − я = ∑ k = 0 п − 1 ∑ я = 0 k + 1 ( п − 1 k + 1 ) ( k + 1 я ) ( п − 1 − я k + 1 − я ) ( − 1 ) k α k + 1 − я ( α я − 1 ) ! ( α ) ( α ( п − 1 − k ) − 1 ) ! ( α ) × ( k + 1 − я ) ! . < displaystyle < begin ( alpha n-1)! _ <( alpha)>& = sum _ ^ sum _ ^ < k + 1> < binom > < binom > (- 1) ^ alpha ^ ( альфа i-1)! _ <( alpha)> < bigl (>alpha (n-1-k) -1 < bigr)>! _ <( alpha)>times (n-1-k ) _ & = sum _ ^ sum _ ^ < binom < к + 1>> < binom > < binom > (- 1) ^ alpha ^ ( alpha i-1)! _ <( alpha)> < bigl (>alpha (n-1-k) -1 < bigr)>! _ <( alpha)>times ( k + 1-i)!. end >>

Первые две суммы выше по форме похожи на известные некруглый комбинаторное тождество для двойной факториальной функции, когда α := 2 данный Каллан (2009).

( 2 п − 1 ) ! ! = ∑ k = 0 п − 1 ( п k + 1 ) ( 2 k − 1 ) ! ! ( 2 п − 2 k − 3 ) ! ! . < displaystyle (2n-1) !! = sum _ ^ < binom > (2k-1) !! (2n-2k-3 ) . >

Дополнительные разложения по конечной сумме сравнений для α -факторные функции, (αn − d)!_(α) , по модулю любого заданного целого числа час ≥ 2 для любого 0 ≤ d даны Шмидт (2017). [21]

Источник

Читайте также:  Что значит двухсотый убитый