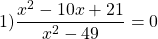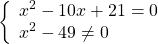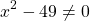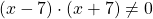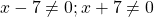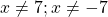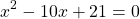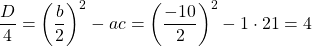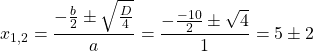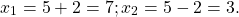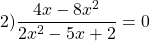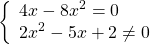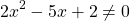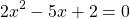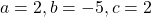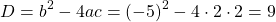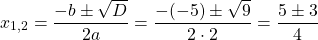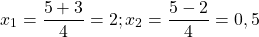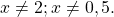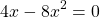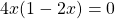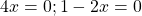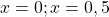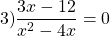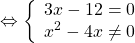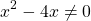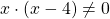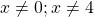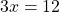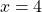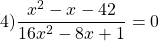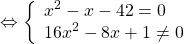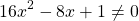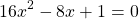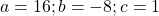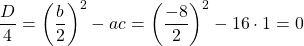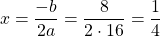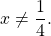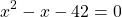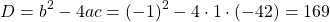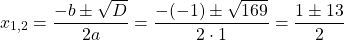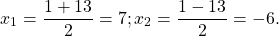Дробь равна нулю что это значит

Содержание

Решение уравнений «дробь равна нулю», описание метода, примеры
В чем состоит метод решения и на чем он базируется?
Обоснование метода
Алгоритм решения уравнений «дробь равна нулю»
Решение примеров
Дробь равна нулю

Решение уравнений «дробь равна нулю», описание метода, примеры

Отдельного внимания заслуживают уравнения «дробь равна нулю», то есть, уравнения f(x)/g(x)=0 , где f(x) и g(x) – произвольные выражения с переменной x . В этой статье мы, во-первых, разберем, в чем состоит метод решения таких уравнений, на чем он базируется и как обосновывается. А во-вторых, запишем алгоритм решения уравнений «дробь равна нулю» и решим несколько характерных примеров.

В чем состоит метод решения и на чем он базируется?

Метод решения уравнений «дробь равна нулю», то есть уравнений, имеющих вид f(x)/g(x)=0 , состоит в нахождении решения через решение уравнения «числитель равен нулю», то есть, через решение уравнения f(x)=0 . Пример для наглядности: решение уравнения можно найти через решения уравнения (x−1)·(x 2 −4)=0 .

Базируется метод на следующем утверждении:

Множество решений уравнения f(x)/g(x)=0 совпадает с множеством решений уравнения f(x)=0 на ОДЗ для уравнения f(x)/g(x)=0 . В частности, решением уравнения 0/g(x)=0 является любое число из ОДЗ для этого уравнения, а уравнение C/g(x)=0 , где С – отличное от нуля число, не имеет решений.

Докажем это утверждение в следующем пункте.

Обоснование метода

В основе доказательства утверждения из предыдущего пункта лежит хорошо известный факт: дробь a/b , b≠0 равна нулю тогда и только тогда, когда ее числитель есть нуль. Этот факт вытекает из определения дроби (дробь a/b , b≠0 есть такое число c , что b·c=a ) и из того, что произведение двух чисел тогда и только тогда равно нулю, когда одно из чисел есть нуль.

Начнем с доказательства частных случаев.

Докажем, что решение уравнения 0/g(x)=0 есть ОДЗ для него. В силу того, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, равенство 0/g(x₀)=0 является верным для любого числа x₀ , при котором оно имеет смысл. Очевидно, что равенство 0/g(x₀)=0 имеет смысл тогда и только тогда, когда x₀ принадлежит ОДЗ для уравнения 0/g(x)=0 . Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.

Докажем, что уравнение C/g(x)=0 , где С – отличное от нуля число, не имеет решений. Так как дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, то равенство C/g(x₀)=0 , C≠0 не может быть верным ни для какого числа x₀ . Следовательно, уравнение C/g(x)=0 , C≠0 не имеет решений.

Теперь будем считать, что числитель дроби f(x)/g(x) есть выражение с переменной, а не число, и докажем, что множество решений уравнения f(x)/g(x)=0 совпадает с множеством решений уравнения f(x)=0 на ОДЗ для уравнения f(x)/g(x)=0 . Для этого достаточно доказать два момента: первый — что любой корень уравнения f(x)/g(x)=0 является корнем уравнения f(x)=0 , второй — что любой корень уравнения f(x)=0 , принадлежащий ОДЗ для уравнения f(x)/g(x)=0 , является корнем уравнения f(x)/g(x)=0 .

Приступаем к доказательству первой части. Пусть x₀ – корень уравнения f(x)/g(x)=0 . Тогда f(x₀)/g(x₀)=0 – верное числовое равенство. Из этого неравенства и из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что f(x₀)=0 . А это равенство означает, что x₀ – корень уравнения f(x)=0 .

Первая часть доказана. Приступаем к доказательству второй части.

Пусть x₀ принадлежит ОДЗ для уравнения f(x)/g(x)=0 и при этом x₀ — корень уравнения f(x)=0 . Так как x₀ принадлежит ОДЗ для уравнения f(x)/g(x)=0 , то дробь f(x₀)/g(x₀) имеет смысл. Так как x₀ – корень уравнения f(x)=0 , то f(x₀)=0 – верное числовое равенство. Из этих результатов, а также из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что дробь f(x₀)/g(x₀) равна нулю, то есть, f(x₀)/g(x₀)=0 . А это равенство означает, что x₀ – корень уравнения f(x)/g(x)=0 .

Так доказана вторая часть и все утверждение в целом.

Алгоритм решения уравнений «дробь равна нулю»

Доказанное утверждение позволяет записать алгоритм решения уравнений «дробь равна нулю»:

Если уравнение имеет вид 0/g(x)=0 , то надо найти область допустимых значений для этого уравнения – она и есть искомое решение уравнения.
Если уравнение имеет вид C/g(x)=0 , C – отличное от нуля число, то сразу записываем ответ – нет решений.
Если уравнение имеет вид f(x)/g(x)=0 , где f(x) – выражение с переменной, а не число, то
- приравниваем числитель к нулю и решаем полученное уравнение f(x)=0 ,
- отсеиваем посторонние корни (отбрасываем все корни, не принадлежащие ОДЗ для исходного уравнения, как посторонние).

Заметим, что записанный алгоритм находится в полном согласии с принципами решения дробно-рациональных уравнений, имеющих вид «дробь равна нулю». Принципы решения таких уравнений раскрываются на уроках алгебры в 8 классе. Оттуда нам известно, что для решения дробно-рационального уравнения, имеющего вид f(x)/g(x)=0 нужно приравнять к нулю числитель, решить полученное уравнение и отбросить те корни, при которых обращается в нуль знаменатель [1, с.26-30]. По сути, отбрасывание значений, при которых обращается в нуль знаменатель решаемого дробно-рационального уравнения f(x)/g(x)=0 , есть отсеивание посторонних корней по ОДЗ, так как в этом случае ОДЗ определяется условием g(x)≠0 .

Решение примеров

Рассмотрим решения трех характерных уравнений «дробь равна нулю»: с нулем в числителе, с отличным от нуля числом в числителе, и с выражением с переменной в числителе. Ими мы закроем все три типичные ситуации.

Сначала решим уравнение с нулем в числителе: .

Решите уравнение

Теперь решим уравнение , в числителе которого отличное от нуля число.

Решите уравнение

Осталось рассмотреть решение уравнения «дробь равна нулю» в случае, когда в числителе находится выражение с переменной, а не число. В этом случае, согласно алгоритму, нужно приравнять к нулю числитель, решить полученное уравнение и отсеять посторонние корни.

Решите уравнение

Источник

Дробь равна нулю

Когда дробь равна нулю?

Дробная черта — это знак деления. При делении нуля на любое число, кроме нуля, получим нуль. На нуль делить нельзя.

Таким образом, дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля.

Решение многих задач в алгебре сводится к решению дробно рациональных уравнений, которые, в свою очередь, сводятся к уравнению типа «дробь равна нулю».

Схематически решение уравнения типа «дробь равна нулю» можно изобразить так:

Таким образом, чтобы решить уравнение типа «дробь равна нулю», надо:

1) Найти значения переменной, при которых знаменатель обращается в нуль.

2) Приравнять к нулю числитель и решить получившееся уравнение.

3) Проверить, нет ли среди корней уравнения «числитель равен нулю» значений, при которых знаменатель обращается в нуль. Если есть, их следует исключить.

4) Записать ответ.

Дробь равна нулю, если числитель равен нулю, а знаменатель — отличен от нуля, поэтому это уравнение равносильно системе

Находим значения переменной, при которых знаменатель обращается в нуль:

Можно приравнять выражение, стоящее в левой части неравенства, к нулю, и решать как обычное неполное квадратное уравнение. Можно решать как уравнение, только вместо знака равенства каждый раз писать «≠».