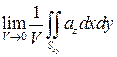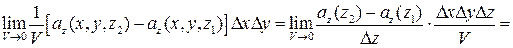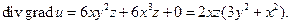Дивергенция, гравитация и Пуассон
Мы уже обсуждали неизбежность закона обратных квадратов в самых естественных предположениях. Ну, если пространство плоско, изотропно и однородно, а силовое поле, создаваемое точечной массой симметрично, потенциально и бездивергентно (в пустом пространстве), то эта сила обратно пропорциональна расстоянию r до тяготеющей массы, а потенциал пропорционален 1/ r . Любые отклонения от этого закона связаны с нарушением каких-то из этих предположений.
И закон Ньютона, и закон Кулона под эту простую схему подпадают.
Теперь рассмотрим более общий случай (хотя одно к другому сводится, конечно). Заодно познакомимся с уравнением Пуассона.
Итак, пусть есть распределение масс: скалярное поле плотности ρ . В каждой точке задано значений плотности. Она создает силу притяжения: силовое поле. В каждой точке задана сила f . Что можно про эту силу сказать?
Пока что угодно! Но пусть поле потенциально, то есть является градиентом некоторого скалярного поля потенциала g (это практически потенциальная энергия). Если поле не потенциально, то в нем нет понятия энергии, работа по замкнутому контуру может быть ненулевой: в общем, это нефизично. Сила трения такая. А гравитация не такая.
Теперь вспомним, что такое дивергенция . Это характеристика векторного поля, показывающая расходимость силовых линий. В терминах потоков (если вектор имеет смысл скорости течения) это поток через границу достаточно малой окрестности точки. Иными словами, дивергенция описывает источники: жидкости или силы. Если силу представить как поток частиц (квантов, гравитонов), то все становится совсем ясно. Источник и производит эти частицы.
Но у нас источниками является плотность. Если непрерывную плотность представить как много-много маленьких тел, материальных точек, то каждая является источником. Тогда можно записать
означает «пропорционально». Подставим одно в другое и получим
Операция divgrad называется оператором Лапласа, а все уравнение — уравнением Пуассона.
Нам даже пока не надо знать, как эти операции выписываются в координатах! Но уравнение уже есть.
Проверим, что все согласуется. Возьмем в качестве ρ дельта-функцию . Если «по-простому», то это такая величина, что она везде нуль, кроме начала координат, но интеграл по любой области, куда это начало входит, равен единице. А если не входит, то равен нулю, естественно. Дельта-плотность соответствует материальной точке: точечной массе или точечному заряду.
Возьмем какой-нибудь шар с центром у нуле и вычислим интеграл по нему от левой и правой части нашего уравнения. Справа получим единицу по «определению» дельты, а слева воспользуемся теоремой Гаусса-Остроградского. Она гласит: интеграл по объему от дивергенции равен потоку через границу объема . Интуитивно это понятно: сумма продукции всех источников выльется через границу наружу. Куда ей еще деваться, если стоки мы все учли? Значит, поток градиента через любую сферу равен единице.
Поток вектора — это надо перпендикулярную к поверхности компоненту вектора умножить на площадь поверхности и сложить по всем кускам поверхности. Для скорости это очевидно, для силы менее, но силу надо представить как поток частиц-переносчиков. Площадь сферы пропорциональна квадрату радиуса, а значит, градиент обратно пропорционален этому квадрату. Всё сошлось.
Но уравнение Пуассона описывает любые распределения, не только дельтавидные. Причем решение для дельты позволяет выписать решение для любой правой части, потому что дельта играет роль «единицы» и из нее можно сложить любую функцию% об этом в другой раз.
К этому уравнению сводится и уравнение Общей теории относительности в предположениях малых скоростей и малых кривизн — как приближение.
Для дивергенции, градиента, оператора Лапласа и других векторных операций есть выражения в популярных координатных системах, и есть общие способы записать их в любых координатах. Так, в декартовых координатах градиент есть вектор из частных производных, дивергенция есть сумма производных i -ой компоненты вектора по i -ой координате, а оператор Лапласа есть сумма вторых производных по каждой координате.
Оператор Лапласа инвариантен относительно вращений: не меняется при вращениях. Он «один» такой, поэтому и встречается во «всех» уравнениях: волновом, теплопроводности/диффузии, Шрёдингера, Пуассона, четырехмерная разновидность появляется в ОТО. Всегда надо смотреть на симметрию! В ней ключ ко всему.
Источник
Просто о градиенте, дивергенции и роторе #96
Есть такие заклинания, которые многие якобы умные люди любят произносить, чтобы «закопать» собеседника, убедив его, что он мало образован. И меня самого не так давно пытались по тому же принципу отправить к изучению уравнений в частных производных. Благо с этими уравнениями я провёл не одну бессонную ночь, потому знаний вполне хватает. Кроме того, эти термины нам пригодятся, чтобы разобраться с новой теорией элементарных частиц и строения атомного ядра .
Для простоты всё будем рассматривать на плоскости и относительно конкретной ситуации, изображённой на рисунке.
Пусть в раковине стоит банка с водой. В боку у неё дырка. Из этой дырки постепенно вытекает вода в объёме порядка двух литров в минуту. А из крана в ту самую банку заливается 3 литра в минуту. Тогда с помощью дифференциальных операторов можно математически довольно точно описать происходящее внутри банки.
Начнём с самого простого, с дивергенции . Её часто записывают, как div F . Сейчас больше употребляют запись вида ∇ ⋅ F . По определению это изменение потока в пределах малого объёма . Т.е. нам нужно собрать всё, что из этого малого объёма (из банки) выходит и вычесть из этого всё, что в этот малый объём входит . Из картинки ясно видно, что имеется 3 литра в минуту входящего потока и 2 литра в минуту – выходящего. Отсюда имеем, что дивергенция внутри банки будет равна -1 . Т.е. выходит на литр меньше, чем заходит. И всё. Никакой магии. Если мы захотим углубиться в этот вопрос, то можно будет привлекать ещё и размеры банки. Т.е. этот объём воды, который притекает в банку, будет как-то распределён по её объёму. Но в данном случае это нам не нужно.
С ротором ( rot F или ∇ × F ) дело несколько сложнее. По определению это циркуляция по малому контуру . Т.е. то, насколько в конкретной точке поток поворачивается . Мы в прошлый раз говорили о векторе угловой скорости. Так вот ротор — это именно угловая скорость, умноженная на два. Как и вектор угловой скорости, ротор направлен перпендикулярно рассматриваемой плоскости, в которой происходит вращение. А величина определяется тем сколько потока при прохождении через банку мы потеряли по Y и сколько приобрели по X. В нашем случае это 3 + 2 = 5 единиц. И если мы взглянем на жёлтую вертушку на рисунке, её будет вращать по направлению фиолетовой стрелки как раз с интенсивностью в 5 наших условных единиц. Сам вектор будет направлен на нас. Т.е. ротором мы называем просто меру поворота некоторого потока . Ничего хитрого.
Ну и наконец градиент ( grad ф или ∇ F . Не путать с дивергенцией ∇ ⋅ F! ). Для начала отметим, что в отличие от ротора и дивергенции градиент характеризует не поток, а некоторую величину вроде температуры или давления и ставит ей в соответствие некоторое векторное поле, которое вполне можно понимать, как некоторый поток. Т.е. ситуация, в общем, обратная. Но мы попробуем за эту величину взять интенсивность нашего потока. Обратимся к определению: градиент – вектор, указывающий направление наибольшего возрастания величины потока, равный по величине изменению этого потока . Т.е. если мы внимательно глянем на нашу банку, то поймём, что справа от банки у нас скорость потока 2 единицы по оси X, а сверху – 3 единицы против оси Y. Т.е. поток изменился на единицу. Значит, длина вектора составит 1. А направление будет совпадать с направлением вектора (-2,3), т.к. интенсивность потока возрастает против его течения.
Если бы мы рассматривали некоторую комнату, в каждой точке внутри которой задано давление, то градиент можно представить, как направление наискорейшего роста давления. Вообще говоря в описанной ситуации против этого градиента будет дуть ветер . И метеорологи определяют направление движения воздушных масс именно с помощью таких градиентов.
Что бы вам не пытались говорить о сложности уравнений в частных производных и прочих понятий, в их основе всегда лежат адекватные достаточно простые положения. И если вам говорят обратное, то скорее всего они либо сами не разобрались, либо просто пытаются ввести вас в заблуждение. Ну а сами роторы и дивергенции — это не более чем удобный способ описания природы, чтобы можно было делать достаточно точные расчёты и делать далеко идущие выводы.
Источник
Дивергенция векторного поля



Особый интерес представляет случай, когда вычисляется поток через замкнутую поверхность. Обычно в таких случаях за положительную сторону поверхности принимают ее внешнюю поверхность. Поверхностный интеграл в этом случае обозначается следующим образом:
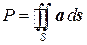
Когда векторное поле a представляет собой поле скоростей жидкости, величина потока P дает разность между количеством жидкости, вытекающей из внутренней области, ограниченной поверхностью S, и количеством, втекающей в эту область. Если P=0, то во внутреннюю область втекает столько же жидкости, сколько и вытекает. Если же P>0, то вытекает больше, чем втекает. Это означает, что внутри области имеются источники, питающие поток жидкости. В случае электрического поля, это означает, что внутри области находятся электрические заряды. Если P
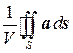
Найдем теперь предел этого отношения, при условии что область, ограниченная поверхностью S, стягивается в точку M, т.е. при V®0. Этот предел называется дивергенцией векторного поля a в точке M:
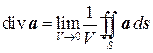
Ясно, что если предел существует, то он не зависит от формы поверхности S.
Дивергенция характеризует мощность источника или стока. Например, если в каждой точке поля скоростей жидкости дивергенция равна нулю, то это означает не только отсутствие источников и стоков, но и то, что жидкость не сжимается и не расширяется. Этим свойством, в частности, обладает воздух при скоростях, не превышающих примерно половины скорости звука. Однако при скоростях близких или превосходящих скорость звука, воздух ведет себя как сжимаемый газ. Тогда дивергенция такого газа будет уже отлична от нуля. Точно также дивергенция отлична от нуля, если в текущем газе возникают химические реакции (например, горение), изменяющие его плотность. В случае гравитационных или электрических полей дивергенция будет пропорциональна плотности масс или зарядов, соответственно.
Выведем теперь формулу для дивергенции в декартовой системе координат. Пусть поверхность S имеет вид прямоугольного параллелепипеда со сторонами Dx, Dy, Dz, параллельного координатным осям (см. рис.6.6). Распишем поверхностный интеграл в определении дивергенции в виде суммы трех двойных интегралов:
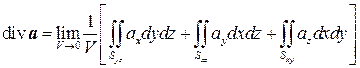
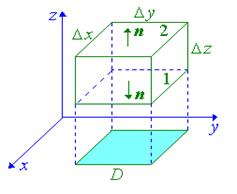 |
| Рис. 6.6 |
Рассмотрим третье слагаемое:
Грани 1 и 2 проецируются в одну и ту же область D на плоскости xOy (боковые грани можно не учитывать, т.к. они перпендикулярны плоскости xOy), однако их внешние нормали направлены в противоположные стороны. Считая, что уравнения граней z=z1 и z=z2, получим
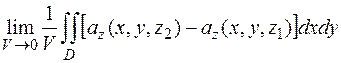
Исходя из геометрического смысла двойного интеграла (это есть объем находящийся между координатной плоскостью и поверхностью, описываемой подынтегральной функцией):
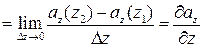
Аналогично можно получить формулы для первого и второго слагаемого в выражении
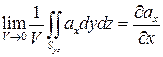
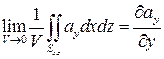
Таким образом, мы доказали следующую теорему:
Теорема. В декартовой системе координат дивергенция векторного поля a = axi+ayj+azk вычисляется по формуле:
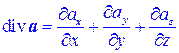
1) Пусть дано однородное поле:a = Ai+Bj+Ck, где A, B, C – постоянные величины. Тогда
div a = 0.
Это означает, что если все части жидкости имеют одну и ту же скорость (т.е. жидкость движется поступательно, как твердое тело), то в таком потоке не может быть ни источников, ни стоков.
2) Пусть твердое тело вращается с постоянной угловой скоростью w. Как известно из теоретической механики линейная скорость равна v=w´r, где r – радиус-вектор точки относительно точки вращения. Если неподвижную точку взять в качестве начала координат, а ось Oz направить вдоль оси вращения, то получим w=wk, r=xi+yj+zk. Тогда
v = –wyi + wxj. (6.8)
Это есть поле линейных скоростей вращающегося твердого тела. Вычислим дивергенцию этого поля:
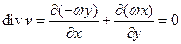
Это означает, что есть представить себе жидкость, вращающейся как твердое тело, то в таком потоке не может быть ни стоков, ни источников.

Пример 6.4. Найти дивергенцию градиента скалярного поля u=x 3 y 2 z в точке M(1;–1;1).
Решение. Найдем градиент поля
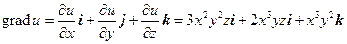
а затем дивергенцию:
Подставляя координаты точки M, получим
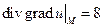
Источник