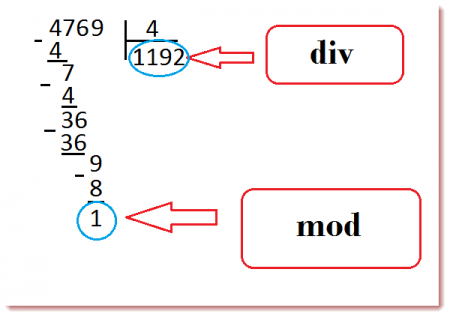
Div 100 mod 10 что значит

Оператор div и оператор mod

В этой статье речь пойдет о целочисленном делении и делении с остатком.

Итак, что такое целочисленное деление вообще? В математике целочисленным делением называют такое деление, при котором одно целое число делится на другое целое число ,а результатом является целая часть их частного.

То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.

Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e

x — число , которое будем делить на y (делимое)
y — число , на которое будем делить число x (делитель)
z — результат целочисленного деления (целочисленное частное)

Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так

z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!

А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.

x — число , которое будем делить на y (делимое)
y — число , на которое будем делить число x (делитель)
z — остаток

Например (40 / 6) с остатком = 4 с оператором mod будет такой

И как результат получим z=1 .

Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.

Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим

Источник

Урок 5. Математические операции, функции и процедуры в Pascal (Часть первая)

Так как в воскресенье на сайте открывается новая рубрика — решение задач, мы с вами должны по-быстрому изучить основную часть математических операций, функций и процедур.

Давайте разберемся, что такое функция и процедура. Это подпрограмма — часть программы, выполняющая определенный алгоритм и допускающая обращение к ней из различных частей общей программы. В чем же разница между процедурой и функцией?

Процедуры — мини-программы.

Процедуры используются в случаях, когда в подпрограмме необходимо получить несколько результатов. Из картинки, расположенной ниже вы видите, как работает процедура. Входных данных может не быть вовсе, а может быть сто.

Например, программист хочет в своем суперкоде между блоками выходящих значений прописывать 20 амперсандов. Чтобы облегчить себе задачу, он напишет простую подпрограмму.

Функции в Паскале — мега переменные.

Функции отличается от процедуры тем, что после выполнения функции на ее месте в коде ставится одно число, буква, строка и т.д. Набор встроенных функций в языке Паскаль достаточно широк. Например, для того, чтобы подсчитать квадрат числа можно воспользоваться стандартной функцией sqr(x). Как вы, наверное, уже поняли sqr(x) требует лишь один фактический параметр — число.

Обратите внимание! Функции необходимо присваивать! Просто написав их в тексте программы, как процедуры, вы ничего не добьетесь!

Структура функции представлена на картинке ниже.

Если в программу необходимо включить новую уникальную функцию, ее надо описать также, как процедуру. Более подробно о том, как делать собственные процедуры и функции, мы поговорим через 10 уроков. Ниже вы видите таблицу основных стандартных функций и процедур в Паскаль.

Имя Тип аргумента Результат вычисления Пример Abs(x) Целый или Вещ. Модуль х Abs(-6) = 6 Sqrt(x) Вещественный Корень из х Sqrt(25)=5 Sqr(x) Целый и Вещ. Квадрат х Sqr(5)=25 Power(x, a) Вещественный Значение х а Power(5,3)=125 Frac(x) Вещественный Дробная часть х Frac(5.67)=0.67 Sin(x) Вещественный Синус х Sin(45)=0.8509 Cos(x) Вещественный Косинус х Cos(45)=0.5253 Arctan(x) Вещественный Арктангенс х Arctan(5)=1.3734 Int(x) Вещественный Целая часть х Int(5.67)=5.0 Random(x) Целый Случайное число (0..х-1) Random(5)=4 Succ(x) Порядковый Следующий Succ(10)=11 Pred(x) Порядковый Предыдущий Pred(‘Z’)=’Y’ Inc(x, a) Целый X:=X+A Inc(5)=6 Dec(x, a) Целый X:=X-A Dec(25,20)=5 Trunc(x) Вещественный Целая часть х Trunc(5.67)=5 Round(x) Вещественный Округление х до целого Round(5.67)=6 Важно! Если х = 5.5, то результат – 6, а если х = 6.5, то результат тоже 6!?

Очень странная ошибка.

Операции div и mod.

Иногда нам требуется найти частное либо же остаток от деления. В такие моменты на помощь нам приходят такие операции, как div и mod. Заметим, что эти операции выполняются только над целыми числами.

Для того, чтобы найти частное от деления, мы используем операцию div.

25 div 20 = 1;
20 div 25 = 0;
39 div 5 = 7;
158 div 3 = 52.

Для того, чтобы найти остаток от деления, мы используем операцию mod.

25 mod 20 = 5;
20 mod 25 = 0;
39 mod 5 = 4;
158 mod 3 = 2.

Чтобы окончательно понять, с чем мы имеем дело, решим следующую задачу:

Задача 1. Найти сумму цифр двухзначного числа.

Так как эта задача очень простая, мы с вами обойдемся блок-схемой и программой.

Блок-схема

Задача 2. Найти сумму цифр трехзначного числа.

Чуть усложненная версия предыдущей задачи. Самая большая сложность — вторая цифра.

Приоритет div и mod больше, чем приоритете + и -. Поэтому в данной программе можно обойтись без скобок.

Источник

Div 100 mod 10 что значит

Рассмотрим подробно арифметические выражения, т. к. именно с их помощью выполняются все вычисления в программе.

Результатом арифметического выражения является целое или вещественное значение. Выражение задает порядок действий над элементами данных и состоит из:

• операндов (констант, переменных, функций);

Арифметические операции

Операции определяют действия, которые надо выполнить над операндами. В отличие от традиционной математической записи обязательно указывать все знаки операций.

Например, в выражении (х+у) *5-10 операндами являются переменные х и у , а также константы 5 и 10 ; а +, * — знаки арифметических операций сложения и умножения соответственно. Символ операции умножения — * (звездочка) должен присутствовать в явном виде. Если все объекты, входящие в выражение, определены в момент их использования (в нашем примере — это переменные х и у ), то значение выражения считается определенным.

В простейшем случае выражение может состоять из одной переменной или константы. Круглые скобки ставятся так же, как и в обычных математических выражениях для управления порядком выполнения операций

При использовании двух знаков операций нежелательно, чтобы они стояли рядом: а*-b . Лучше заключить второй операнд в скобки: а*(-b) .

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Операции DIV и MOD

Целочисленное деление div (от division, деление) отличается от обычной операции деления тем, что возвращает целую часть частного, а дробная часть отбрасывается — 13 div 3 = 4 , а не 4,(3). Результат div всегда равен нулю, если делимое меньше делителя.

Взятие остатка от деления mod (от modulus, мера) вычисляет остаток, полученный при выполнении целочисленного деления.

Аргументы операций div и mod — целые числа. Взаимосвязь между операциями div и mod проста. Для а>0 и b>0 справедливо:

A mod b = a – (a div b)*b

(a div b)*b + (a mod b) = a

Обратите внимание — операцию mod можно использовать, чтобы узнать, кратно ли целое а целому b . А именно, а кратно b тогда и только тогда,когда а mod b = 0 (см. лиcтинг 3.6).

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Арифметические процедуры и функции

В арифметических выражениях часто используются следующие стандартные функции (табл. 3.1).

Стандартная функция	Выполняемое действие	Тип
		аргумента	результата
abs (x)	\|x\|	real	real
		integer	integer
sqr (x)	x 2	real	real
		integer	integer
sqrt (x)	x 1/2	real	real
		integer	real
exp (x)	e x	real	real
		integer	real
ln (x)	ln (x)	real	real
		integer	real
sin (x)	sin (x)	real	real
		integer	real
cos (x)	cos (x)	real	real
		integer	real
arctan (x)	arctg (x)	real	real
		integer	real
pi	число Π	—	real

Вызов стандартной функции осуществляется путем указания в нужном месте программы имени функции ( аbs, ln, ехр и др.) и ее аргумента, заключенного в круглые скобки. После вычисления значения функции ее вызов заменяется результатом, и расчет содержащего ее выражения продолжается дальше (см. листинг 3.1).

• аргумент прямых тригонометрических функций sin и соs задается в радианах. Для преобразования значения угла из радианной меры в градусную необходимо умножить величину угла на число 180/рi . Для перевода значения угла из градусной меры в радианную необходимо умножить величину угла на число pi/180 (см. листинг 3.1);

• результат функции агсtаn получается в радианах.

Кроме приведенных в табл.3.1 также используются следующие стандартные процедуры и функции:

• функция random ( диапазон) возвращает случайное число х , удовлетворяющее условию 0 . Тип аргумента и результата — word . В том случае, если нам необходимы целые случайные числа из диапазона b>x>=a ,мы можем получить их, используя выражение random (b-a)+a . Если параметр диапазон не указан, то random возвращает число х в диапазоне 0 . Тип результата — rеа1 . В том случае, если нам необходимы вещественные случайные числа из другого диапазона: b>x>=а , мы можем задать его при помощи random*b+a . Перед первым обращением к функции random необходимо с помощью вызова процедуры randomize инициализировать программный генератор случайных чисел. В противном случае при каждом запуске программы датчик будет выдавать одни и те же числа. Эту особенность можно использовать при отладке программы;

• процедура dec(х,n) уменьшает значение целочисленной переменной х на n . Например, х:=10; dec (х, 2); <результат: 8>. При отсутствии необязательного параметра n процедура принимает вид deс(х) , а значение х уменьшается на единицу;

• процедура inc(х,n) увеличивает значение целочисленной переменной х на n . Например, х:=10; inc(х,3); <(результат: 13>. При отсутствии необязательного параметра n процедура принимает вид inс (х) , а значение х увеличивается на единицу;

• функция frас(х) вычисляет дробную часть х . Аргумент и результат — rеа1 . Например write (frас(0.25*11) :4:2); <результат 0.75>;

• функция int (х) вычисляет целую часть х . Аргумент и результат — rеа1 . Например, write(int(422.117) :4:2) ; <результат 422.00>. Таким образом, х=int (х) +frас (х) .

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Функции TRUNC и ROUND

При работе с целочисленной арифметикой нельзя смешивать операнды целого и вещественного типов. Пусть i — переменная целого типа, а х — вещественного. Тогда для получения целочисленного результата их суммирования необходимо воспользоваться одной из функций trunc или round : trunc (х) ИЛИ round (х) .

• Функция преобразования типа trunc(х) возвращает ближайшее целое число, меньше или равное вещественному х для х>=0 , и больше или равное х для х (от truncate, усекать). Таким образом, выполняется отбрасывание десятичных знаков после точки. Аргумент — rеа1 , результат — longint .

• Функция преобразования типа round(х) возвращает значение х , округленное до ближайшего целого числа (от round, круглый). Аргумент — rеа1 , результат — longint .

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Возведение в степень

Вычисление степени числа выполняется в Тurbо Раsсаl с использованием свойств логарифмов:

Таким образом, нельзя возвести в степень отрицательное число. Для этого можно использовать операторы циклов.

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Полезные формулы

Для вычисления логарифма с основанием а используем:

В Тurbо Раsсаl определены только три тригонометрические функции: sin, соs, аrсtg (табл. 3.1). Для вычисления остальных тригонометрических, функций необходимо использовать известные соотношения:

&nbspменю &nbsp &nbsp &nbsp &nbsp вверх

Приоритет операций

Последовательность выполнения операций в составе выражения происходит с учетом их приоритета (старшинства). В табл. 3.2 приведен порядок выполнения всех основных операций (арифметических и логических). Подробнее о логических операциях будет рассказано ниже (см. разд. 3.8.1).

Таблица 3.2. Порядок выполнения основных операций

Операция	Приоритет	Вид операции
not, @	Первый (высший)	Унарная операция
*, /, div, mod, and, shl, shr	Второй	Операции типа умножения
+, —, or, xor	Третий	Операции типа сложения
=, , , =, in	Четвертый	Операции отношения

Обратите внимание — операции с равным приоритетом выполняются слева направо. Выражение, заключенное в скобки, перед выполнением вычисляется как отдельный операнд. При наличии вложенных скобок вычисления выполняются, начиная с самых внутренних. В тексте программы необходимо проверять парность расстановки скобок: число открывающих скобок должно быть равно числу закрывающих скобок.

• в выражении 3+4*5 умножение * выполняется перед сложением + , потому что его приоритет выше. Для изменения порядка используйте скобки: (3+4) *5 ;

• выражения а*b/с и (а*b) /с вычисляются одинаково, т. к. приоритеты умножения и деления равны, а знак операции умножения стоит левее знака деления. Для изменения порядка действий необходимы скобки: а*(Ь/с) .

Листинг 3.1 содержит программу вычисления площади треугольника по двум сторонам и углу между ними. Угол вводится в градусах и переводится в радианы.

Процедура clrscr очищает экран и помещает курсор в его левый верхний угол. Для того чтобы процедура clrscr была доступна программе, в ее начало помещается строка uses crt; .

Листинг 3.2 содержит программу, которая вычисляет месячные выплаты m по займу в s рублей на n лет под процент р . Вычисления выполняются по формулам:

Листинг 3.2. Вычисление ежемесячных выплат по займу

Для преобразования числа в денежный формат (выделения рублей и копеек) в программе используются операции div и mod . Обратите внимание, что в тексте программы трижды повторяется пара операторов для выделения значений рублей и копеек ( rub и кор ), при этом меняется только имя переменной: s, m, d (заем, выплата и прибыль). Возникает закономерный вопрос: можно ли записать эти операторы один раз, а затем трижды «вызвать» их для вычисления результата — переменных rub и кор , подставляя каждый раз имена различных исходных данных — переменных s, m и d .

Листинг 3.3 содержит программу, вычисляющую сумму цифр трехзначного числа.

Листинг 3.3. Вычисление суммы цифр трехзначного числа

&nbspпредыдущая&nbsp &nbsp &nbsp &nbsp &nbspменю &nbsp &nbsp &nbsp &nbsp вверх &nbsp &nbsp &nbsp &nbsp &nbspследующая

Источник