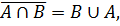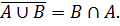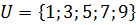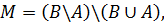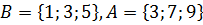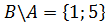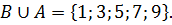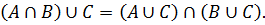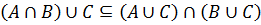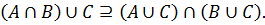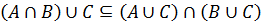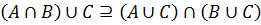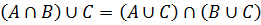Что значит задать множество пересечением элементов

Введение в теорию множеств и комбинаторику

Практическая работа № 1. Способы задания множеств

Вопросы к работе

1. Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.

2. Что значит задать множество?

3. Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.

4. Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.

5. Дайте определение характеристического свойства элементов множества.

Образцы решения заданий

Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.

Ответ: .

Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:

. Ответ: М = <1; 2; 3; 4>.

Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:

Приведите примеры множеств, составленных из объектов следующих видов:

а) неодушевленных предметов;

г) геометрических фигур;

д) населенных пунктов;

ж) политических деятелей.

2. Назовите элементы, принадлежащие множеству:

а) студентов вашей группы;

б) предметов, изучаемых в I семестре вашей специальности;

в) всех частей света;

г) субъектов федерации, входящих в Российскую Федерацию.

3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:

4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:

а) 270 N ; ж) -3 Z ;

б) 0 N ; з) Q ;

в) –3 N ; и) R ;

г) 1 Q ; к) sin 2,3 R ;

д) –7 N ; л) tg R .

е) 22 N ;

6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?

а) Франция Е ; з) Волга Е ;

б) Испания Е ; и) Нигерия А ;

в) Монголия А ; к) Гималаи А ;

г) Индия А ; л) Япония А ;

д) Ирак Е ; м) Альпы Е ;

е) Турция А ; н) Швеция А .

ж) Байкал А ;

7. Запишите перечислением элементов следующие множества:

а) А – множество нечетных чисел на отрезке [1; 15];

б) В – множество натуральных чисел, меньших 8;

в) С – множество натуральных чисел, больших 10, но меньших 12;

г) D – множество двузначных чисел, делящихся на 10;

д) Е – множество натуральных делителей числа 18;

е) F – множество чисел, модуль которых равен .

8. Запишите перечислением элементов следующие множества:

а) множество различных букв в слове «головоломка»;

б) множества цифр числа 134433154.

9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x :

10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:

Прочитайте следующие записи и перечислите элементы каждого из множеств:

Источник

Пересечение, объединение и разность множеств

Пересечение множеств

Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:

Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.

Если A = $\$ — натуральные числа, кратные 3, B = $\$ — натуральные числа, кратные 5, то $A \cap B = $ — натуральные числа, кратные 15.

Если A = , B = , то $A \cap B = \varnothing$.

Объединение множеств

Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:

Если $B \subseteq A$ — подмножество, то $A \cap B = A$ – объединением будет большее множество из двух.

Универсум и отрицание

Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.

В литературе универсум обозначают U.

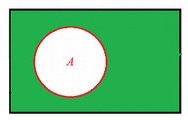
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:

При рассмотрении целочисленных задач, универсум – это множество целых чисел.

При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.

При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.

Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:

У отрицания есть любопытное свойство: $\bar<\bar<Α>> = Α $(два раза «нет» — это «да»).

Если U = $\$ — все действительные числа, A = $\$ — все положительные действительные числа, то $ \bar = \$.

Свойства операций пересечения и объединения

$A \cap B = B \cap A$

$ A \cup B = B \cup A $

$(A \cap B) \cap C = A \cap (B \cap C)$

$ (A \cup B) \cup C = A \cup ( B \cup C) $

$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$

$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $

Взаимодействие с отрицанием, пустым множеством и универсумом

$A \cap \varnothing = \varnothing$

$A \cup \varnothing = A$

Законы де Моргана

$ (A \cup B) \cap A = A $

$ (A \cap B) \cup A = A $

Разность множеств

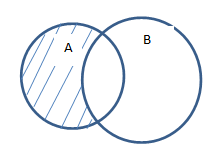
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:

Читается «A без B».

На диаграммах Эйлера разности для пересекающихся множеств выглядят так:

Получается, что отрицание – частный случай разности: $ \bar = \ $= U\A

«Не A» — это «универсум без A».

Формулы включений и исключений

Рассмотрим два конечных пересекающихся множества A и B.

Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.

Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?

Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:

$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$

Выведем аналогичную формулу для трёх пересекающихся конечных множеств.

Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».

$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$

$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$

Примеры

Пример 1. Найдите пересечение данных множеств:

Источник

Пересечение и объединение множеств — свойства, операции и примеры решения

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств. Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.

То, из чего состоит множество, называется его элементами.

Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.

Что такое пересечение множеств

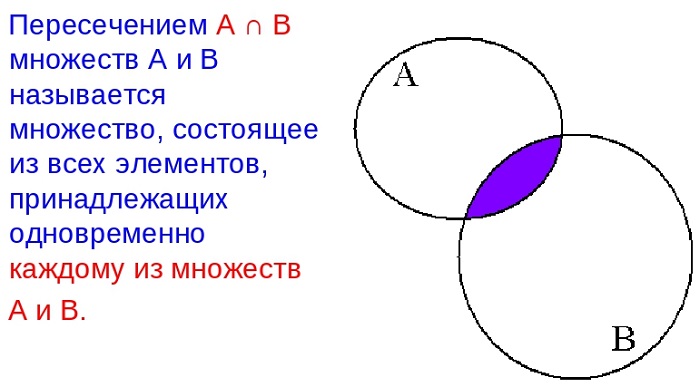
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.

С помощью кругов Эйлера-Венна пересечение можно изобразить так:

Часто применяется для определения решений систем уравнений и неравенств.

Ассоциируется с обычным умножением двух числовых объектов.

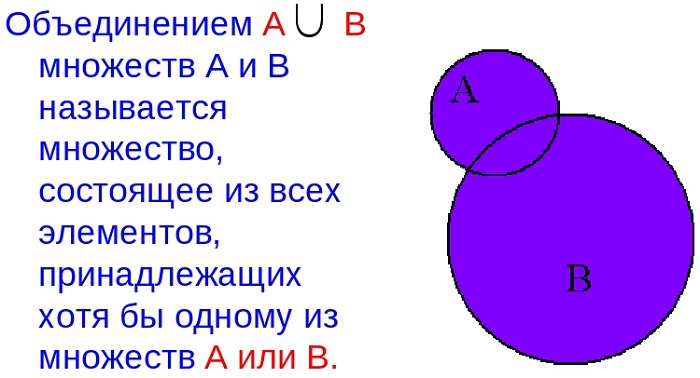
Что такое объединение множеств

Изображение кругами Эйлера выглядит следующим образом:

Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.

В обычной математике близко по смыслу с операцией, называемой «сложение».

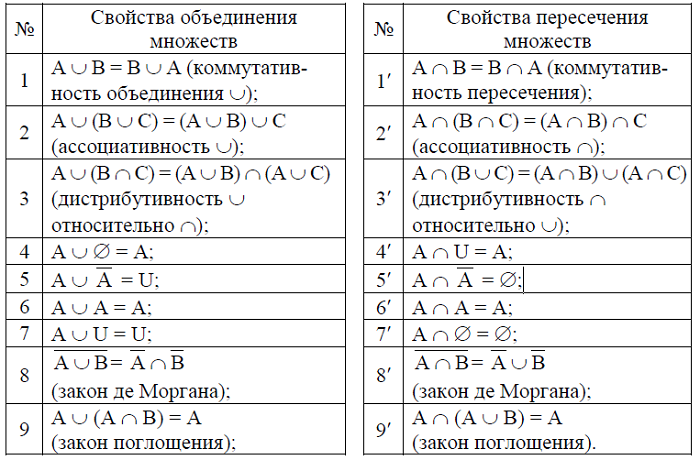
Свойства пересечения и объединения множеств

Для решения задач нужно знать о следующих свойствах:

1. Коммутативность (перестановочность):

Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.

2. Ассоциативность (расстановка скобок):

(A ∩ B) ∩ C = A ∩ (B ∩ C);

(A ∪ B) ∪ C = A ∪ (B ∪ C).

Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.

3. Дистрибутивность (раскрытие скобок):

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).

4. Закон идемпотентности (идентичности):

Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø

Выполнение операций с Ø:

Прослеживается аналог со сложением и умножением на ноль.

Операции над множествами

Помимо объединения и пересечения существуют другие операции:

Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:

Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:

Благодаря этой операции свойства объединения и пересечения можно расширить/

Закон де Моргана:

Примеры решения задач

Задача №1

Выписать все элементы множества

При поиске M операции выполняются последовательно.

B \ A состоит из всех элементов B, которые не принадлежат A, поэтому:

B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:

M = (B \ A) \ (B ∪ A) состоит из всех элементов B \ A, которые не принадлежат B ∪ A, следовательно, M = Ø.

Задача №2

Доказать методом включений тождество:

Необходимо доказать выполнение включений:

Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.

Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.

Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).

Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).

Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:

Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).

По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.

Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.

Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.

Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть

Из пунктов 1 и 2 вытекает, что

Источник