Что значит высота пирамиды

Высота пирамиды

Объем пирамиды коротко о главном

Пирамида – это многогранник, который состоит из любого плоского многоугольника (основание пирамиды), точки, не лежащей в плоскости основания, (вершина пирамиды) и всех отрезков, соединяющих вершину пирамиды с точками основания.

Треугольники, в которые «сливаются» эти отрезки, называются боковыми гранями, а отрезки, проведённые к вершинам основания — это боковые ребра.

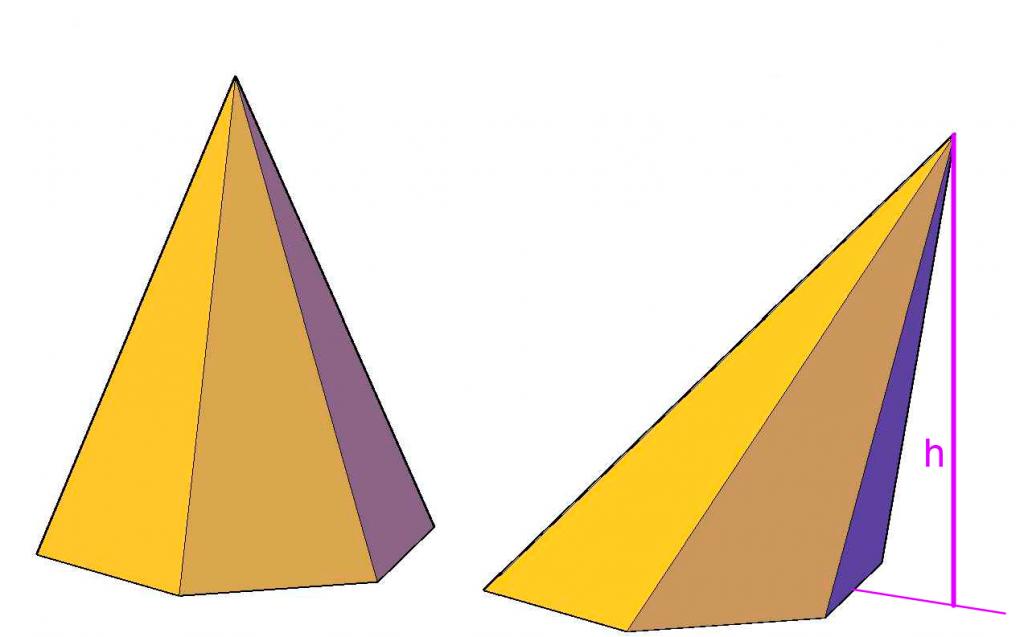
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Правильная пирамида — пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

• В правильной пирамиде все боковые рёбра равны.
• Все боковые грани – равнобедренные треугольники и все эти треугольники равны.

Элементы пирамиды

Элементами этой геометрической фигуры являются:

Место, куда сходятся все боковые грани фигуры, является вершиной.

Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.

Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.

Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.

На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.

Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.

У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.

Объем пирамиды

Главная формула объема пирамиды

Откуда взялась именно \( \displaystyle \frac<1><3>\)?

Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac<1><3>\), а у цилиндра – нет.

Теперь давай посчитаем объем самых популярных пирамид.

Свойства правильной пирамиды

У такой фигуры можно отметить особые свойства.

У правильной пирамиды все боковые треугольники одинаковы.

Каждая из них является равнобедренным треугольником.

Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.

Снаружи возможна сфера, касающаяся всех вершин.

Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.

Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.

Формулы для высоты правильной пирамиды

Существует четыре основных линейных характеристики для любой пирамиды правильной:

• сторона основания;
• боковое ребро;
• апофема боковой грани;
• высота фигуры.

Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — hb и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:

h = √(ab2 — a2/4);h = √(b2 — a2/2).

Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.

Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:

Источник

Высота пирамиды: определение, формулы, расчеты

Одной из объемных фигур, изучаемых в курсе пространственной геометрии, является пирамида. Важной характеристикой этой фигуры является ее высота. В статье дадим определение высоты пирамиды и приведем формулы, через которые она связана с другими линейными характеристиками.

Что собой представляет пирамида

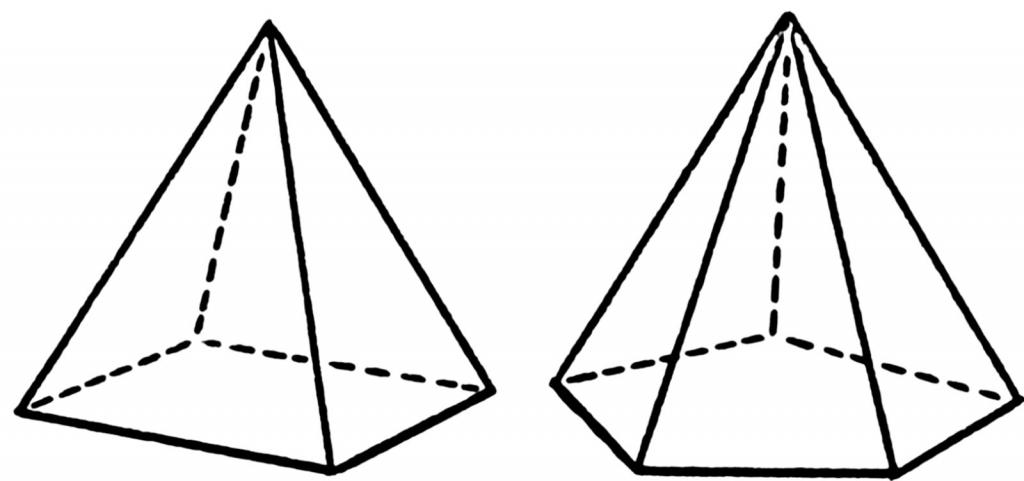
Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.

Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.

Высота фигуры

Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды — это единственный перпендикуляр, который является одной из важных ее линейных характеристик.

Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма — точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.

Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.

Важными свойствами всех правильных пирамид являются следующие:

• все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
• длины боковых ребер и апофем являются одинаковыми.

Формулы для высоты правильной пирамиды

Существует четыре основных линейных характеристики для любой пирамиды правильной:

• сторона основания;
• боковое ребро;
• апофема боковой грани;
• высота фигуры.

Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — h_b и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:

Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.

Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:

Решение задачи с шестиугольной пирамидой

Предположим, что нам дана пирамида правильная с шестиугольным основанием. Известно, что высота основания пирамиды равна 13 см. Зная, что длина ее бокового ребра равна 10 см, необходимо вычислить объем и высоту правильной шестиугольной пирамиды.

Рисунок ниже показывает, как выглядит правильный шестиугольник.

Расстояние между любыми его двумя параллельными сторонами называется высотой. Не сложно показать, что эта высота h_a связана с длиной стороны фигуры следующей формулой:

Подставляя в выражение значение h_a, находим, что сторона основания a равна 7,51 см.

Высоту h фигуры можно определить, если рассмотреть прямоугольный треугольник, находящийся внутри пирамиды и состоящий из двух катетов (высота пирамиды и половина диагонали шестиугольного основания) и гипотенузы (боковое ребро). Тогда значение h будет равно:

Объем пирамиды определяется как третья часть от произведения высоты фигуры на площадь ее основания. Площадь правильного шестиугольника равна:

S₆ = n/4*a 2 *ctg(pi/n) = 6/4*a 2 *ctg(pi/6) = 3*√3/2*a 2 = 3*√3/2*56,4 ≈ 146,53 см 2 .

Использованная для вычисления S₆ формула является универсальной для произвольного правильного n-угольника.

Для определения объема фигуры остается подставить в соответствующую формулу найденные параметры:

Мы получили значение высоты пирамиды и рассчитали ее объем. Таким образом, поставленная задача решена.

Источник

Объем пирамиды (ЕГЭ 2022)

В этой статье вы поймете что такое пирамида и какими они бывают.

Вы научитесь вычислять объем пирамиды, высоту и другие ее параметры.

Вы научитесь решать задачу на доказательство (ЕГЭ №14) и записывать доказательства так, чтобы не сняли баллы на ЕГЭ.

Объем пирамиды — коротко о главном

Определение пирамиды:

Пирамида – это многогранник, который состоит из любого плоского многоугольника (основание пирамиды), точки, не лежащей в плоскости основания, (вершина пирамиды) и всех отрезков, соединяющих вершину пирамиды с точками основания.

Треугольники, в которые «сливаются» эти отрезки, называются боковыми гранями, а отрезки, проведённые к вершинам основания — это боковые ребра.

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Правильная пирамида — пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

Свойства правильной пирамиды:

• В правильной пирамиде все боковые рёбра равны.
• Все боковые грани – равнобедренные треугольники и все эти треугольники равны.

Объем пирамиды:

Что такое пирамида

Как она выглядит?

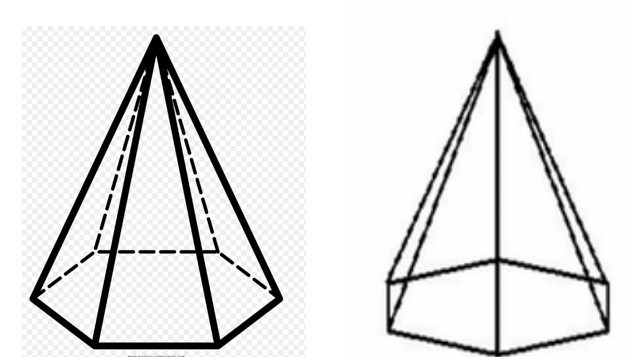
Вместо того, чтобы читать длинное определение, достаточно просто посмотреть на картинку:

Видишь: у пирамиды внизу (говорят «в основании») какой-нибудь многоугольник, и все вершины этого многоугольника соединены с некоторой точкой в пространстве (эта точка называется «вершина»).

У всей этой конструкции ещё есть боковые грани, боковые рёбра и рёбра основания.

Ещё раз нарисуем пирамиду вместе со всеми этими названиями:

Некоторые пирамиды могут выглядеть очень странно, но всё равно это – пирамиды.

Вот, например, совсем «косая» пирамида.

И ещё немного о названиях: если в основании пирамиды лежит треугольник, то пирамида называется треугольной, если четырёхугольник, то четырёхугольной, а если стоугольник, то … догадайся сам.

Высота пирамиды

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

При этом точка, куда oпустилась высота, называется основанием высоты.

Обрати внимание, что в «кривых» пирамидах высота может вообще оказаться вне пирамиды.

И ничего в этом страшного нет. Похоже на тупоугольный треугольник.

Правильная пирамида

Правильной называется такая пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

Много сложный слов?

Давай расшифруем: «В основании – правильный многоугольник» — это понятно.

А теперь вспомним, что у правильного многоугольника есть центр – точка, являющаяся центром и вписанной, и описанной окружности.

Ну вот, а слова «вершина проецируется в центр основания» означают, что основание высоты попадает как раз в центр основания. Смотри, как ровненько и симпатично выглядит правильная пирамида.

Шестиугольная правильная пирамида

В основании – правильный шестиугольник, вершина \( \displaystyle S\) проецируется в центр основания.

Четырехугольная правильная пирамида

В основании – квадрат, вершина \( \displaystyle S\) проецируется в точку пересечения диагоналей этого квадрата.

Треугольная правильная пирамида

В основании – правильный треугольник, вершина \( \displaystyle S\) проецируется в точку пересечения высот (они же и медианы, и биссектрисы) этого треугольника.

Очень важные свойства правильной пирамиды

В правильной пирамиде:

• Все боковые ребра равны
• Все боковые грани – равнобедренные треугольники и все эти треугольники равны.

Объем пирамиды

Главная формула объема пирамиды

Откуда взялась именно \( \displaystyle \frac<1><3>\)?

Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac<1><3>\), а у цилиндра – нет.

Теперь давай посчитаем объем самых популярных пирамид.

Объем правильной треугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle <_<осн>>\) и \( \displaystyle H\).

\( \displaystyle <_<осн>>\) – это площадь правильного треугольника \( \displaystyle ABC\).

Вспомним, как искать эту площадь.

Используем формулу площади:

\( \displaystyle S=\frac<1><2>ab\cdot \sin \gamma \)

У нас «\( \displaystyle a\)» – это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60<>^\circ =\frac<\sqrt<3>><2>\)

Теперь найдем \( \displaystyle H\).

По теореме Пифагора для \( \displaystyle \Delta SOC\)

Чему же равно \( \displaystyle OC\)?

Это радиус описанной окружности в \( \displaystyle \Delta ABC\), потому что пирамида правильная и, значит, \( \displaystyle O\) — центр \( \displaystyle \Delta ABC\)

Найдем \( \displaystyle OC\) (Подробнее смотри в теме «Правильный треугольник»).

\( \displaystyle OC=\frac<2><3>CK\), так как \( \displaystyle O\) — точка пересечения и медиан тоже.

\( \displaystyle C<^<2>>=A<^<2>>-A<^<2>>\) (теорема Пифагора для \( \displaystyle \Delta ACK\))

Подставим \( \displaystyle OC\) в формулу для \( \displaystyle H\).

И подставим все в формулу объема:

Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:

Объем правильной четырехугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).

Здесь \( \displaystyle <_>\) и искать не нужно; ведь в основании – квадрат, и поэтому \( \displaystyle <_>=<^<2>>\).

Найдем \( \displaystyle H\). По теореме Пифагора для \( \displaystyle \Delta SOD\)

Известно ли нам \( \displaystyle OD\)? Ну, почти. Смотри:

Подставляем \( \displaystyle OD\) в формулу для \( \displaystyle H\):

А теперь и \( \displaystyle H\) и \( \displaystyle <_>\) подставляем в формулу объема.

Объем правильной шестиугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).

Как найти \( \displaystyle <_>\)? Смотри, шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете объема правильной треугольной пирамиды, здесь используем найденную формулу.

Теперь найдем \( \displaystyle H\) (это \( \displaystyle SO\)).

По теореме Пифагора для \( \displaystyle \Delta SOE\)

Но чему же равно \( \displaystyle OE\)? Это просто \( \displaystyle a\), потому что \( \displaystyle \Delta EOF\) (и все остальные тоже) правильный.

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео мы разобрали следующие вопросы:

• Как нарисовать шестиугольную пирамиду и как исправить рисунок, если грани пирамиды сливаются.
• Как правильно подписать вершины пирамиды.
• Как доказать пункты А и Б задания №14 из ЕГЭ и записать доказательство так, чтобы не сняли баллы на экзамене.
• Как найти площадь основания пирамиды (чтобы найти объем) и правильно записать решение.
• Как найти объем пирамиды.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь попробуй ты!

Мы рассказали тебе все о пирамидах. Не о тех, что строили инопланетяне и рептилоиды, но все же… Сделали это не хуже всяких конспирологических каналов!

Теперь ты можешь быть уверен, что у тебя есть хорошая база для решения большинства задач стереометрии. И ты не зайдешь в тупик прямо со слов «В правильном тетрадэдре PABCD…»

А теперь слово тебе. Расскажи нам, понравилась ли тебе статья? Были ли трудности?

Напиши нам ниже в комментариях!

А еще можешь задавать любые вопросы. Мы читаем все и обязательно ответим.

Источник

Читайте также:  Что значит высокие гранулоциты