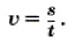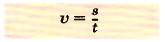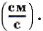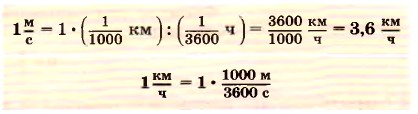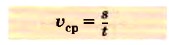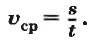Что значит выразить скорость тела

§ 16. Скорость. Единицы скорости

Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Например, по шоссе шагает турист, мчится автомобиль, в воздухе летит самолёт. Допустим, что все они движутся равномерно, тем не менее движение этих тел будет отличаться.

Автомобиль движется быстрее пешехода, а самолёт быстрее автомобиля. В физике величиной, характеризующей быстроту движения тел, является скорость.

Предположим, что турист за 1 ч проходит 5 км, автомобиль 90 км, а самолёт пролетает 850 км. Тогда говорят, что скорость туриста 5 км в час, скорость автомобиля 90 км в час, а скорость самолёта 850 км в час.

Скорость при равномерном движении тела показывает, какой путь оно прошло в единицу времени.

Таким образом, используя понятие скорости, мы можем теперь сказать, что турист, автомобиль и самолёт движутся с различными скоростями.

При равномерном движении скорость тела остаётся постоянной.

Если велосипедист проезжает в течение 5 с путь, равный 25 м, то его скорость будет равна 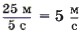(5 метров в секунду).

Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени.

Скорость обозначают буквой υ, путь — s, время — t.

Формула для нахождения скорости будет иметь вид:

• Скорость тела при равномерном движении — это величина, равная отношению пути ко времени, за которое этот путь пройден.

В Международной системе (СИ) скорость измеряют в метрах в секунду

Это значит, что за единицу скорости принимается скорость такого равномерного движения, при котором за 1 секунду тело проходит путь, равный 1 метру.

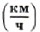
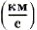
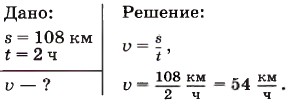
Скорость тела можно измерять также в километрах в час ; километрах в секунду ; сантиметрах в секунду

П р и м е р. Поезд, двигаясь равномерно, за 2 ч проходит путь, равный 108 км. Вычислите скорость движения поезда.

Запишем условие задачи и решим её.

Выразим скорость поезда в единицах СИ, т. е. километры переведём в метры, а часы в секунды:

Таким образом, числовое значение скорости зависит от выбранной единицы.

Скорость, кроме числового значения, имеет и направление.

Если требуется узнать, где будет находиться через 2 ч самолёт, вылетевший из Владивостока, то необходимо знать не только значение его скорости, но и её направление.

Величины, которые, кроме числового значения (модуля), имеют ещё и направление, называют векторными.

Скорость — это векторная физическая величина.

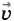
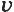
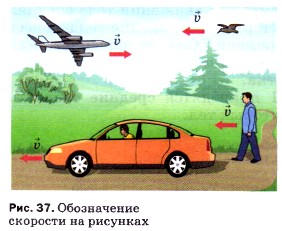
Все векторные величины обозначают соответствующими буквами со стрелочкой. Например, скорость обозначается буквой со стрелочкой, а её значение — модуль скорости той же буквой, но без стрелочки .

На рисунках стрелкой показывают направление скорости, т. е. направление движения тела (рис. 37).

Некоторые физические величины не имеют направления. Они характеризуются только числовым значением. Это путь, время, объём, длина и др. Они являются скалярными величинами.

Если при движении тела его скорость изменяется от одного участка пути к другому, то такое движение является неравномерным.

Для характеристики неравномерного движения тела вводят понятие средней скорости.

Например, поезд от Москвы до Санкт-Петербурга идёт со скоростью 80 км/ч. Какую скорость имеют в виду? Ведь скорость поезда на остановках равна нулю, после остановки — увеличивается, а перед следующей остановкой — уменьшается.

В данном случае поезд движется неравномерно, а значит, скорость, равная 80 км/ч, — это средняя скорость движения поезда. Она определяется почти так же, как и скорость при равномерном движении.

Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на всё время движения:

Следует напомнить, что только при равномерном движении отношение 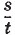за любой промежуток времени будет постоянно.

При неравномерном движении тела средняя скорость характеризует движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в различные моменты времени этого промежутка.

В таблице 1 приводятся средние скорости движения некоторых тел.

Вопросы

1. Что показывает скорость тела при равномерном движении?
2. По какой формуле определяют скорость тела, если известен его путь и время, за которое он пройден?
3. Какова единица измерения скорости в СИ?
4. Чем, кроме числового значения, характеризуется скорость тела?
5 Как определяют среднюю скорость при неравномерном движении?

Упражнение 3

1. Выразите скорости тел: 90км/ч и 36 км/ч в м/с.
2. Поезд идёт со скоростью 72 км/ч. Выразите его скорость в м/с.
3. Гоночный автомобиль за 10 мин проезжает путь, равный 50 км. Определите его среднюю скорость.
4. Лучшие конькобежцы дистанцию 1500 м пробегают за 1 мин 52,5 с. С какой средней скоростью они проходят эту дистанцию?
5. Лыжник, спускаясь с горы, проходит 50 м за 5 с. Спустившись с горы и продолжая двигаться, он до полной остановки проходит ещё 30 м за 15 с. Найдите среднюю скорость лыжника за всё время движения.

Задание

Найдите с помощью Интернета фамилии советских лётчиков, совершивших впервые в мире беспосадочный перелёт Москва—Северный полюс—США. Известно, что расстояние 8582 км они пролетели за 63 ч 16 мин. Определите, с какой скоростью летел самолёт.

Источник

Как переводить скорость в систему СИ

Приборы для измерения скорости автомобилей измеряют скорость в километрах в час. В системе СИ принято измерять скорость в метрах в секунду. Разберем, как переводить скорости в систему СИ.

Примечания:

• Прибор, измеряющий скорость автомобиля, называется спидометром;
• Скорость — это один из параметров, описывающих движение. Движение может быть равномерным, или равнопеременным, или более сложным, например, колебательным.

Километры в час в метры в секунду

Рассмотрим два способа перевода единиц, один – с помощью формулы, второй – с помощью заранее подготовленного списка.

Способ 1 – с помощью формулы

\( \displaystyle v_ \left( \frac<\text<км>><\text<ч>> \right) \) – скорость, выраженная в километрах в час;

\( \displaystyle v_ \left( \frac<\text<м>> \right) \) – скорость, выраженная в метрах в секунду;

В одном километре помещается 1000 метров.

В одном часе содержится 3600 секунд.

Пример 1. Самолет движется со скоростью 420 километра в час. Переведем эту скорость в метры в секунду.

Решение:

Для удобства разложим числа на множители:

\[ \large v_ = 6 \cdot 7 \cdot 10 \cdot \frac<10> <6 \cdot 6>\]

Произведем сокращения и получим точный ответ:

\[ \large v_ = 7 \cdot 10 \cdot \frac<5> <3>= \frac<350> <3>\]

В некоторых случаях точный ответ можно округлить:

Ответ:

\[ \displaystyle \large v_ = 116<,>67 \left( \frac<\text<м>> \right)\]

Способ 2 – с помощью списка

Километры в час в метры в секунду можно достаточно быстро переводить в уме, применяя такой список:

\[ \large \boxed < \begin3<,>6 \left( \frac<\text<км>> <ч>\right) = 1 \left( \frac<\text<м>> \right) \\ 7<,>2 \left( \frac<\text<км>> <ч>\right) = 2 \left( \frac<\text<м>> \right) \\ 10<,>8 \left( \frac<\text<км>> <ч>\right) = 3 \left( \frac<\text<м>> \right) \\ 14<,>4 \left( \frac<\text<км>> <ч>\right) = 4 \left( \frac<\text<м>> \right) \end > \]

\[ \large \boxed < \begin18 \left( \frac<\text<км>> <ч>\right) = 5 \left( \frac<\text<м>> \right) \\ 36 \left( \frac<\text<км>> <ч>\right) = 10 \left( \frac<\text<м>> \right) \\ 54 \left( \frac<\text<км>> <ч>\right) = 15 \left( \frac<\text<м>> \right) \\ 72 \left( \frac<\text<км>> <ч>\right) = 20 \left( \frac<\text<м>> \right) \end > \]

Пример 2. Автомобиль движется по трассе со скоростью 108 километров в час. Переведем эту скорость в метры в секунду.

Решение:

108 км/ч = 72 км/ч + 36 км/ч = 20 м/с + 10 м/с

Ответ:

Переводим метры в секунду обратно в километры в час

Иногда возникает необходимость перевести скорость из метров в секунду в километры в час. Чтобы проделать это, используем такую формулу:

Скорости более медленных объектов

Скорость движения медленных объектов, например, некоторых живых существ – улиток, измеряется в сантиметрах в минуту. Перевести такие единицы в систему СИ также, достаточно легко.

\( \displaystyle v_ \left( \frac<\text<км>><\text<ч>> \right) \) – скорость, выраженная в сантиметрах в минуту;

\( \displaystyle v_ \left( \frac<\text<м>> \right) \) – скорость, выраженная в метрах в секунду;

В одном метре помещается 100 сантиметров. А 1 сантиметр – это 0,01 метра.

В одной минуте содержится 60 секунд.

Пример 3. Улитка перемещается со скоростью 6 сантиметров в минуту. Переведем эту скорость в метры в секунду.

Решение:

Раскладываем числа на множители:

Сократим числа и получим ответ:

Ответ:

\[ \displaystyle \large v_ = 0<,>001 \left( \frac<\text<м>> \right)\]

Выводы

Для перевода скорости в систему СИ можно использовать любой удобный прием – либо воспользоваться формулой перевода, либо, заранее подготовить список некоторых значений скоростей, а затем представить переводимую скорость в виде суммы, складывая числа из списка;

Источник

Скорость. Единицы скорости

Содержание

Механическое движение имеет множество характеристик. Вы уже узнали, что оно относительно и бывает разных видов: прямолинейное и криволинейное, равномерное и неравномерное.

Тела движутся по воображаемым линиям, которые называются траекториями, а длина траектории – это путь, который проходит тело.

В этом уроке мы рассмотрим новую физическую величину, характеризующую движение – скорость.

Скорость при равномерном движении

Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?

Рисунок 1. Разные физические тела, совершающие равномерное движение.

В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь, в физике, появляется такая величина, как скорость.

Скорость – это физическая величина, характеризующая быстроту движения тел

В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, т.е. движутся с различными скоростями.

Скорость при равномерном движении тела показывает, какой путь проходит тело в единицу времени

Скорость при равномерном движении постоянна

Как вычислить скорость

Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:

$$\upsilon = \large \frac$$

где $\upsilon$ – скорость, $S$ – путь, $t$ – время.

Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.

Соответственно, если автомобиль проезжает в течение 10 с путь, равный 20 метрам, то его скорость будет равна $\frac<20 м> <10 с>= 2 \frac<м><с>$ (2 метра в секунду).

Скорость при неравномерном движении

При неравномерном движении тело проходит разные пути за равные промежутки времени, т.е. скорость тела изменяется от одного участка пути к другому.

Как же определить скорость на всем пути? Здесь нам поможет понятие средней скорости.

Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:

Отметим, что средняя скорость описывает движение тела за весь промежуток времени. В это время тело можно замедляться, разгоняться, останавливаться.

Например, если вы выезжаете на автомобиле из Москвы в Санкт-Петербург (рисунок 2), то весь путь займет у вас 10 ч. В это время машина будет то набирать скорость, то тормозить, сделает остановку. Общий путь, который вы при этом проедите, будет равен 600 км.

Средняя скорость движения автомобиля будет равна:
$\upsilon_ <ср>= \frac = \frac<600 км> <10 ч>= 60 \frac<км><ч>$.

Рисунок 2. Пример неравномерного движения.

Взгляните на таблицу 1, где приведены различные средние скорости.

Тело	Скорость	Тело	Скорость
Улитка	0,0014	Пассажирский самолет	220
Черепаха	0,05-0,14	Звук в воздухе при $0 \degree C$	332
Муха	5	Пуля автомата Калашникова	760
Пешеход	1,5	Луна вокруг Земли	1000
Конькобежец	13	Молекула водорода при $0 \degree C$	1693
Скворец	20	Молекула водорода при $25 \degree C$	1770
Страус	22	Земля вокруг Солнца	30 000
Автомобиль	20	Свет и радиоволны	300 000 000

Средние скорости движения некоторых тел, скорость звука, радиоволн и света, $\frac<м><с>$.

Единицы измерения скорости

В Международной системе (СИ) скорость измеряется в метрах в секунду $\frac<м><с>$.

За за единицу скорости принимают скорость такого равномерного движения, при котором за 1 секунду тело проходит путь длиной 1 метр.

Следственно, скорость в системе СИ – количество метров, которое тело пройдёт за 1 секунду.

В повседневной жизни мы чаще видим, что скорость измеряют в километрах в час $\frac<км><ч>$. Также можно использовать километры в секунду $\frac<км><с>$ и сантиметры в секунду $\frac<см><с>$.

Наиболее часто встречаемое ограничение скорости в городах – $ 60 \frac<км><ч>$. Переведем это значение в $\frac<м><с>$:

Так мы увидели, что числовое значение скорости зависит от выбранной единицы измерения.

Скорость как вектор

Логично, что, кроме числового значения, скорость имеет и направление. Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.

Физические величины делятся на те, которые имеют направление и те, которые его не имеют – на векторные и скалярные:

1. Векторные величины – это величины, которые, кроме числового значения (модуля), имеют еще и направление.

Скорость – это векторная физическая величина

Векторные величины обозначаются буквами со стрелочками. Скорость обозначается как $\vec<\upsilon>$, а модуль скорости – $\upsilon$.

На рисунке 3 стрелкой показано направление скорости (направление движение тела).

Рисунок 3. Направление скорости для различных тел.

2. Скалярные величины – это физические величины, которые не имеют направления и характеризуются только числовым значением. Это путь, объем, время, длина, масса и др.

Примеры задач на нахождение скорости

1. Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.

Дано:
$S = 152 км$
$t = 3 ч$

Найти:
$\upsilon -?$

Показать решение и ответ

Решение:
$\upsilon = \frac$
$\upsilon = \frac<152> <3>\frac<км> <ч>\approx 51 \frac<км> <ч>$.

Выразим в единицах СИ:
$51 \frac<км> <ч>= \frac<51 000> <3600>\frac<м> \approx 14 \frac<м>$.

Ответ: $\upsilon = 14 \frac<м><с>$.

2. Скорость лыжника первую часть пути составляла $20 \frac<км><ч>$ в течение 15 мин. Следующие 45 мин его скорость была $10 \frac<км><ч>$. Найдите среднюю скорость лыжника.

Обозначим первую часть пути как $s_1$, вторую как $s_2$. Время, соответствующее движению на этих участках, $t_1$ и $t_2$ (рисунок 4). Скорости – $\upsilon_1$ и $\upsilon_2$.

Рисунок 4. Схема движения лыжника.

Дано:
$\upsilon_1 = 20 \frac<км><ч>$
$t_1 = 15$ мин
$\upsilon_2 = 10 \frac<км><ч>$
$t_2 = 45$ мин

Найти:
$\upsilon_ <ср>-?$

Показать решение и ответ

Решение:
Скорость лыжника на первой и второй частях пути:
$\upsilon_1 = \frac$; $\upsilon_2 = \frac$.

Выразим из этих уравнений неизвестные $s_1$ и $s_2$:
$s_1 = \upsilon_1t_1$; $s_2 = \upsilon_2t_2$

Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:
$\upsilon_ <ср>= \frac = \frac<\upsilon_1t_1+\upsilon_2t_2>< t_1+t_2>$.

Выпишем отдельно часть выражения и переведем в часы:
$t_1+t_2 = 15$ мин $+$ $45$ мин = $1$ ч.

Тогда:
$t_1 = \frac<1><4>$ ч $= 0,25$ ч
$t_2 = \frac<3><4>$ ч $= 0,75$ ч

Ответ: $\upsilon_ <ср>= 12,5 \frac<км><ч>$.

Источник

Читайте также:  Что значит мобильный билет