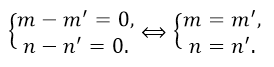Что значит выписать координаты векторов

Содержание

Как найти координаты вектора
Предварительные сведения
Готовые работы на аналогичную тему
Координаты вектора
Линейные операции над векторами
Пример задачи на нахождение координат вектора
Метод координат (ЕГЭ 2022)
Метод координат — коротко о главном
Система координат
Векторы
Координаты вектора
Действия с векторами
Расстояние между двумя точками на координатной плоскости
Координаты середины отрезка
Умножение векторов

Как найти координаты вектора

Вы будете перенаправлены на Автор24

Предварительные сведения

Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.

Доказательство.

Возможны два случая:

Из этого всего следует, что $\overrightarrow=k\overrightarrow$.

Из этого всего следует, что $\overrightarrow=k\overrightarrow$.

Лемма доказана.

Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:

Доказательство.

Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:

Вектор $\overrightarrow$ коллинеарен (к примеру) вектору $\overrightarrow$.

По лемме 1, будем иметь

Значит, если число $m=0$, то получим

Вектор $\overrightarrow$ не коллинеарен векторам $\overrightarrow$ и $\overrightarrow$.

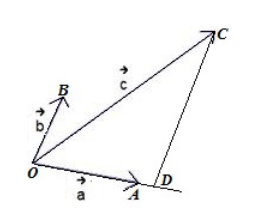
Возьмем произвольную точку $O$ и отложим от нее векторы $\overrightarrow=\overrightarrow,\ \overrightarrow=\overrightarrow$ и $\overrightarrow=\overrightarrow$. Пусть Проведем прямую $CD||OB$ (рис. 1)

Рисунок 1. Иллюстрация теоремы 1

По правилу треугольника для сложения векторов, получим

Готовые работы на аналогичную тему

Следовательно, разложение единственно.

Теорема доказана.

Координаты вектора

Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $\overrightarrow$, а в направлении оси $Oy$ отложим вектор $\overrightarrow$, длины которых равны единице.

Векторы $\overrightarrow$ и $\overrightarrow$ называются координатными векторами.

Так как векторы $\overrightarrow$ и $\overrightarrow$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $\overrightarrow=m\overrightarrow+n\overrightarrow$.

Коэффициенты разложения вектора $\overrightarrow=m\overrightarrow+n\overrightarrow$ называются координатами данного вектора в данной системе координат, то есть

Линейные операции над векторами

Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.

Доказательство.

Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow=\left\$, $\overrightarrow=\$, тогда

Теорема доказана.

Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.

Доказательство.

Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow=\left\$, $\overrightarrow=\$, тогда

Теорема доказана.

Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.

Доказательство.

Теорема доказана.

Пример задачи на нахождение координат вектора

Решение.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2021

Источник

Метод координат (ЕГЭ 2022)

Метод координат — это твоя «палочка-выручалочка»! Он позволит тебе свести многие задачи по геометрии к простой алгебре.

Метод в особенности хорош, когда ты неуверенно чувствуешь себя в построении пространственных фигур, сечений и т. д.

Конечная цель статьи – научить тебя пользоваться методом координат, чтобы решать задачи ЕГЭ повышенной сложности для трехмерных фигур.

Давай с ним разберемся!

Метод координат — коротко о главном

Вектор – направленный отрезок. $ \displaystyle A$ — начало вектора, $ \displaystyle B$-конец вектора.
Вектор обозначается $ \displaystyle a$ или $ \displaystyle \overline$.

Абсолютная величина вектора – длина отрезка, изображающего вектор. Обозначается, как $ \displaystyle \left| a \right|$.

Координаты вектора $ \displaystyle a$:

Произведение векторов: \( \displaystyle \lambda \overline(<_<1>>,\text< ><_<2>>)\text< >=

Скалярное произведение векторов: Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними:

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв).

Система координат

С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.

Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции $ y=ax+b$, например, $ y=2-3$.

Напомню, ты строил ее по точкам. Помнишь?

Ты выбирал произвольное число $ x$, подставлял ее в формулу $ y=2-3$ и вычислял таким образом $ y$.

Например, если $ x=0$, то $ y=2\cdot 0-3=-3$, если же $ x=1$, то $ y=2\cdot 1-3=-1$и т. д.

Что же ты получал в итоге?

А получал ты точки с координатами: $ A\left( 0,-3 \right)$ и $ B\left( 1,-1 \right)$.

Далее ты рисовал «крестик» (систему координат $ X0Y$), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции $ y=2-3$.

Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:

Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке;

Принято, что ось $ \displaystyle X$ идет слева направо, а ось $ \displaystyle Y$ – cнизу вверх;

Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой $ \displaystyle O$;

В записи координаты точки, например $ \displaystyle A\left( 0,-3 \right)$, слева в скобках стоит координата точки по оси $ \displaystyle X$, а справа, по оси $ \displaystyle Y$. В частности, $ \displaystyle A\left( 0,-3 \right)$ просто означает, что у точки $ \displaystyle A$ $ \displaystyle x=0,

y=-3.$;
Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа);

Для любой точки, лежащей на оси $ \displaystyle Ox,$, $ \displaystyle y=0.$;

Для любой точки, лежащей на оси $ \displaystyle Oy$, $ \displaystyle x=0.$;

Ось $ \displaystyle Ox$ называется осью абсцисс;

Ось $ \displaystyle Oy$ называется осью ординат.

Векторы

Теперь давай с тобой сделаем следующий шаг: отметим две точки $ \displaystyle A\left( <_<1>>,<_<1>> \right)$ $ \displaystyle B\left( <_<2>>,<_<2>> \right)$.

Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки $ \displaystyle A$ к точке $ \displaystyle B$:

То есть мы сделаем наш отрезок направленным!

Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!

Вектором называется направленный отрезок, имеющий начало и конец.

Таким образом, если мы соединим точку $ \displaystyle A$ c точкой $ \displaystyle B$, причем началом у нас будет точка A, а концом – точка B, то мы получим вектор $ \displaystyle \overrightarrow$.

Это построение ты тоже делал в 8 классе, помнишь?

Координаты вектора

Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора.

Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты?

Оказывается, что да! И делается это очень просто:

Координаты вектора = координаты точки конца – координаты точки начала.

Таким образом, так как в векторе $ \displaystyle \overrightarrow$ точка $ \displaystyle A\left( <_<1>>,<_<1>> \right)$ – начало, а $ \displaystyle B\left( <_<2>>,<_<2>> \right)$ – конец, то вектор $ \displaystyle \overrightarrow$ имеет следующие координаты:

Например, если $ \displaystyle A\left( 2,0 \right)$$ \displaystyle B\left( 1,2 \right)$, то координаты вектора $ \displaystyle \overrightarrow$

$ \displaystyle \overrightarrow\left( 1-2,2-0 \right)=\overrightarrow\left( -1,2 \right)$

Теперь давай сделаем наоборот, найдем координаты вектора $ \displaystyle \overrightarrow$.

Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке $ \displaystyle B$, а конец – в точке $ \displaystyle A$.

$ \displaystyle \overrightarrow\left( 2-1,\text< >\!\!

Посмотри внимательно, чем отличаются векторы \( \displaystyle \overrightarrow$ и $ \displaystyle \overrightarrow$?

Единственное их отличие – это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:

Иногда, если не оговаривается специально, какая точка является началом вектора, а какая – концом, то векторы обозначают не двумя заглавными буквами, а одной строчной, например: $ \displaystyle <\vec>$, $ \displaystyle <\vec
>$ и т. д.

Еще больше о векторах и проекциях (эту тему мы непременно затронем) ты можешь прочитать в статье по физике «Большая теория по векторам» 🙂

Теперь немного потренируйся сам и найди координаты следующих векторов:

K\left( 0,-3 \right)\);
$ \displaystyle \overrightarrow

K\left( 2,3 \right)$;
$ \displaystyle \overrightarrow

C\left( 0,\sqrt <2>\right),

Проверка:

\( \displaystyle \overrightarrow\left( -1,-5 \right)$;

$ \displaystyle \overrightarrow\left( 3,3 \right)$;

$ \displaystyle \overrightarrow\left( -2,\sqrt<2>-3 \right)$.

А теперь реши задачку чуть посложнее:

Вектор $ \displaystyle \overrightarrow$ с началом в точке $ \displaystyle A\left( 2;

4 \right)$ имеет координаты $ \displaystyle \left( 6;

2 \right)$. Найдите абсциссу точки $ \displaystyle B$.

Решение:

Все тоже довольно прозаично: пусть $ \displaystyle (x,y)$ – координаты точки $ \displaystyle B$. Тогда

Систему я составил по определению того, что такое координаты вектора. Тогда точка $ \displaystyle B$ имеет координаты $ \displaystyle \left( 8,6 \right)$. Нас интересует абсцисса. Тогда

Ответ: $ \displaystyle 8$

Действия с векторами

Что еще можно делать с векторами?

Да почти все то же самое, что и с обычными числами:

Векторы можно складывать друг с другом;

Векторы можно вычитать друг из друга;

Векторы можно умножать (или делить) на произвольное ненулевое число;

Векторы можно умножать друг на друга.

Что же происходит при выполнении этих действий с координатами векторов?

1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты.

2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:

Сложение и вычитание векторов (визуализация)

Кстати, все эти операции имеют вполне наглядное геометрическое или визуальное представление.

Например, правило треугольника (или параллелограмма) для сложения и вычитания.

Сложение векторов по правилу треугольника:

Вычитание векторов по правилу треугольника:

Сложение векторов по правилу параллелограмма:

Вектор растягивается или сжимается или меняет направление при умножении или делении на число:

Например:

Найдите сумму координат вектора $ \vec+\vec$.

Вектор растягивается или сжимается или меняет направление при умножении или делении на число:

Давай вначале найдем координаты каждого из векторов.

Оба они имеют одинаковое начало – точку начала координат. Концы у них разные.

Тогда сумма координат полученного вектора равна $ 20$.

Ответ: $ 20$

Теперь реши сам следующую задачу:

Найти сумму координат вектора $ 3\vec-2\vec$

Ответ: $ 0$

Расстояние между двумя точками на координатной плоскости

Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?

Обозначим расстояние между ними через $ d$. Давай сделаем для наглядности следующий чертеж:

А также из точки $ <
_<1>>$ провел линию, параллельную оси $ Ox$, а из точки $ <
_<2>>$ провел линию, параллельную оси $ Oy$.

Они пересеклись в точке $ R$, образовав при этом замечательную фигуру. Чем она замечательна?

Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!

Искомый отрезок – это гипотенуза этого треугольника, а отрезки $ <
_<1>>R,

Чему равны координаты точки \( R$?

Да, их несложно найти по картинке: $ R\left( <_<2>>,<_<1>> \right).

Так как отрезки \( <
_<1>>R,

<
_<2>>R$ параллельны осям $ Ox$ и $ Oy$ соответственно, то их длины легко найти: если обозначить длины отрезков $ <
_<1>>R,

<
_<2>>R$ соответственно через \( \left| <
_<1>>R\left| ,

Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:

Таким образом, расстояние между двумя точками – это корень из суммы квадратов разностей из координат.

Или же – расстояние между двумя точками – это длина отрезка, их соединяющего.

Легко заметить, что расстояние между точками не зависит от направления.

Отсюда делаем три вывода:

Длина вектора = корень из суммы квадратов его координат;

Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);

Длины векторов, соединяющих две точки в разном направлении, равны.

Давай немного поупражняемся в вычислении расстояния между двумя точками:

Например, если $ A\left( 1,2 \right),

B\left( 3,4 \right)$, то расстояние между $ A$ и $ B$ равно

Или пойдем по-другому: найдем координаты вектора $ \overrightarrow$

$ \overrightarrow\left( 3-1,4-2 \right)=\overrightarrow\left( 2,2 \right)$

И найдем длину вектора:

Как видишь, одно и то же!

Теперь немного потренируйся сам:

Задание. Найти расстояние между указанными точками:

B\left( 5,2\sqrt <3>\right)\);
$ C\left( 2,4 \right),

D\left( 1,-5 \right)$;
$ F\left( \sqrt<12>,1 \right),

Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:

1. Найдите квадрат длины вектора \( \vec-\vec$.

2. Найдите квадрат длины вектора $ \overrightarrow$

Я так думаю, ты с ними без труда справился? Проверяем:

1. А это на внимательность) Мы уже нашли координаты векторов $ \displaystyle <\vec>$ и $ \displaystyle <\vec>$ ранее: $ \displaystyle \vec\left( 2,6 \right),

2. Найдем координаты вектора \( \displaystyle \overrightarrow=\overrightarrow\left( 8-2,6-4 \right)=\overrightarrow\left( 6,2 \right)$

Тогда квадрат его длины равен

Ничего сложного, правда? Обычная арифметика, не более того.

Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.

Задача 1. Найдите синус угла наклона отрезка, соединяющего точки $ \displaystyle O\left( 0;

0 \right)$,$ \displaystyle A\left( 6;

8 \right)$ с осью абсцисс.

Как мы будем поступать здесь?

Нужно найти синус угла между $ \displaystyle OA$ и осью $ \displaystyle Ox$.

А где мы умеем искать синус? Верно, в прямоугольном треугольнике.

Так что нам нужно сделать? Построить этот треугольник!

Поскольку координаты точки $ \displaystyle A-6$ и $ \displaystyle 8$, то отрезок $ \displaystyle OB$ равен $ \displaystyle 6$, а отрезок $ \displaystyle AB-8$.

Нам нужно найти синус угла $ \displaystyle \angle AOB$.

Напомню тебе, что синус – это отношение противолежащего катета к гипотенузе, тогда

$ \displaystyle sin\angle AOB=\frac$

Что нам осталось сделать?

Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!).

Я пойду вторым путем:

$ \displaystyle sin\angle AOB=\frac=\frac<8><10>=0.8$

Ответ: $ \displaystyle 0.8$

Следующая задача покажется тебе еще проще. Она – на координаты точки.

Задача 2. Из точки $ \displaystyle A\left( 6;8 \right)$ опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.

Давай сделаем рисунок:

Основание перпендикуляра – это та точка, в которой он пересекает ось абсцисс (ось $ \displaystyle Ox$) у меня это точка $ \displaystyle B$.

По рисунку видно, что $ \displaystyle B$ имеет координаты: $ \displaystyle B\left( 6,0 \right)$.

Нас интересует абсцисса – то есть «иксовая» составляющая. Она равна $ \displaystyle 6$.

Ответ: $ \displaystyle 6$.

Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки $ \displaystyle A$ до осей координат.

Задача – вообще элементарная, если знать, что такое расстояние от точки до осей.

Я надеюсь, но все же напомню тебе:

Расстояние от точки до осей координат – это длины перпендикуляров, опущенных из точки к осям.

Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр. К какой он оси?

К оси $ \displaystyle Ox$.

И чему же равна тогда его длина?

Она равна $ \displaystyle 8$.

Теперь сам проведи перпендикуляр к оси $ \displaystyle Oy$ и найди его длину. Она будет равна $ \displaystyle 6$, ведь так?

Тогда их сумма равна $ \displaystyle 14$.

Ответ: $ \displaystyle 14$.

Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке $ \displaystyle A$ относительно оси абсцисс.

Я думаю, тебе интуитивно ясно, что такое симметрия?

Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д.

Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой.

А что тогда такое ось?

Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии – прямая $ \displaystyle l$):

Теперь давай вернемся к нашей задаче.

Нам известно, что мы ищем точку, симметричную относительно оси $ \displaystyle Ox$.

Тогда эта ось – ось симметрии.

Попробуй сам отметить такую точку. А теперь сравни с моим решением:

У тебя получилось так же?

Хорошо! У найденной точки нас интересует ордината.

Она равна $ \displaystyle -8$

Ответ: $ \displaystyle -8$

А теперь скажи мне, подумав $ \displaystyle 10$ секунд, чему будет равна абсцисса точки, симметричной точке A относительно оси ординат?

Каков твой ответ? Правильный ответ: $ \displaystyle -6$.

В общем случае правило можно записать вот так:

Ну и теперь совсем страшная задача: найти координаты точки, симметричной точке $ \displaystyle A$, относительно начала координат.

Ты вначале подумай сам, а потом посмотри на мой рисунок!

Ответ: $ \displaystyle \left( -6,-8 \right)$

Теперь задачка на параллелограмм:

Задача 5. Точки $ \displaystyle O\left( 0;

$ являются вершинами параллелограмма. Найдите ординату точки $ \displaystyle B$.

Можно решать эту задачу двумя способами: логикой и методом координат.

Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.

Совершенно ясно, что абсцисса точки $ \displaystyle B$ равна $ \displaystyle 6$. (она лежит на перпендикуляре, проведенной из точки $ \displaystyle A$ к оси абсцисс).

Нам нужно найти ординату.

Воспользуемся тем, что наша фигура – параллелограмм, это значит, что $ \displaystyle CA=OB$.

Найдем длину отрезка $ \displaystyle CA$, используя формулу расстояния между двумя точками:

Опускаем перпендикуляр, соединяющий точку $ B$ с осью $ Ox$.

Точку пересечения обозначу буквой $ D$.

Длина отрезка $ OD$ равна $ 6$. (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка $ BD$ по теореме Пифагора:

Длина отрезка – в точности совпадает с его ординатой.

Ответ: $ 2$.

Другое решение (я просто приведу рисунок, который его иллюстрирует)

Провести $ CE$;

Найти координаты точки $ E$ и длину $ AE$;

Доказать, что $ BD=AE$.

Еще одна задачка на длину отрезка:

2 \right)\) являются вершинами треугольника. Найдите длину его средней линии $ CD$, параллельной $ OA$.

Ты помнишь, что такое средняя линия треугольника?

Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника – это линия, которая соединяет середины противоположных сторон.

Она параллельна основанию и равна его половине.

Основание – это отрезок $ OA$.

Его длину нам приходилось искать ранее, оно равно $ 10$.

Тогда длина средней линии вдвое меньше и равна $ 5$.

Ответ: $ 5$.

Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.

А пока – вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!

1. Точки $ O\left( 0;

6 \right)$ являются вершинами трапеции. Найдите длину ее средней линии $ DE$.

2. Точки $ O\left( 0;

6 \right)$ и $ A$ являются вершинами параллелограмма. Найдите ординату точки $ A$.

3. Найдите длину отрезка, соединяющего точки $ A\left( 6 ;

8 \right)$ и $ B\left( -2;

4. Найдите площадь закрашенной фигуры на координатной плоскости.

5. Окружность с центром в начале координат проходит через точку \( \displaystyle P\left( 8;\text< >6 \right)$. Найдите ее радиус.

6. Найдите радиус окружности, описанной около прямоугольника $ \displaystyle ABCD$, вершины которого имеют координаты соответственно $ \displaystyle \left( -2;

Решения:

1. Известно, что средняя линия трапеции равна полусумме ее оснований.

Основание \( \displaystyle CB$ равно $ \displaystyle 6$, а основание $ \displaystyle OA-10$.

Тогда $ \displaystyle ED=\frac<2>=\frac<16><2>=8$

Ответ: $ \displaystyle 8$

2. Проще всего решить эту задачу так: заметить, что $ \displaystyle \overrightarrow=\overrightarrow+\overrightarrow$ (правило параллелограмма).

Вычислить координаты векторов $ \displaystyle \overrightarrow$ и $ \displaystyle \overrightarrow$ не представляет труда: $ \displaystyle \overrightarrow\left( 2,6 \right),

\overrightarrow\left( 8,2 \right)$.

При сложении векторов координаты складываются.

Тогда $ \displaystyle \overrightarrow$ имеет координаты $ \displaystyle \left( 10,8 \right)$.

Эти же координаты имеет и точка $ \displaystyle A$, поскольку начало вектора $ \displaystyle \overrightarrow$ – это точка с координатами $ \displaystyle \left( 0,0 \right)$.

Нас интересует ордината. Она равна $ \displaystyle 8$.

Ответ: $ \displaystyle 8$

3. Действуем сразу по формуле расстояния между двумя точками:

Ответ: $ \displaystyle 10$

4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область?

Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького.

Сторона маленького квадрата – это отрезок, соединяющий точки $ \displaystyle \left( 0,2 \right)$ и $ \displaystyle \left( 2,0 \right).$ Его длина равна

Тогда площадь маленького квадрата равна

Точно так же поступаем и с большим квадратом: его сторона – это отрезок, соединяющий точки $ \displaystyle \left( 0,4 \right)$ и $ \displaystyle \left( 4,0 \right).$

Его длина равна

Тогда площадь большого квадрата равна

Площадь искомой фигуры найдем по формуле:

Ответ: $ \displaystyle 24$

5. Если окружность имеет в качестве центра начало координат и проходит через точку $ \displaystyle P$, то ее радиус $ \displaystyle R$ будет в точности равен длине отрезка $ \displaystyle OP$ (сделай рисунок и ты поймешь, почему это очевидно).

Найдем длину этого отрезка:

Ответ: $ \displaystyle 10$

6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали.

Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)

$ \displaystyle R=\frac<1><2>\left| AC \right|=5$

Ответ: $ \displaystyle 5$

Ну что, ты со всем справился?

Было не очень сложно разобраться, ведь так? Правило здесь одно – уметь сделать наглядную картинку и просто «считать» с нее все данные.

Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить:

как найти координаты середины отрезка и

Координаты середины отрезка

Давай попробуем решить вот такую нехитрую задачку.

Пусть даны две точки $ \displaystyle A\left( <_<1>>,<_<2>> \right)

Найти координаты середины отрезка \( \displaystyle AB$. Решение этой задачки следующее: пусть точка $ \displaystyle D$ – искомая середина, тогда $ \displaystyle D$ имеет координаты:

То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.

Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:

1. Найдите ординату середины отрезка, соединяющего точки $ \displaystyle A\left( 6,

$ и $ \displaystyle B\left( -2,

2. Точки \( \displaystyle O\left( 0;

6 \right)$ являются вершинами четырехугольника. Найдите ординату точки $ \displaystyle P$ пересечения его диагоналей.

3. Найдите абсциссу центра окружности, описанной около прямоугольника $ \displaystyle ABCD$, вершины которого имеют координаты соответственно $ \displaystyle \left( -2;

Решения:

1. Первая задачка – просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты \( \displaystyle \left( \frac<6-2><2>,

Ордината равна \( \displaystyle 5$.

Ответ: $ \displaystyle 5$

2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой.

Что я знаю про параллелограмм?

Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей – это что?

Это середина любой из диагоналей!

Выберу, в частности диагональ $ \displaystyle OA$. Тогда точка $ \displaystyle P$ имеет координаты $ \displaystyle \left( \frac<6+0><2>,\frac<8+0> <2>\right)=\left( 3,4 \right).$

Ордината точки $ \displaystyle P$ равна $ \displaystyle 4$.

Ответ: $ \displaystyle 4$

3. С чем совпадает центр описанной около прямоугольника окружности?

Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника?

Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей.

Возьму, например, диагональ $ \displaystyle AC$. Тогда если $ \displaystyle P$ – центр описанной окружности, то $ \displaystyle P$ – середина $ \displaystyle AC$.

Ищу координаты: $ \displaystyle P\left( \frac<-2+6><2>,\frac<-2+4> <2>\right)=P\left( 2,1 \right).$ Абсцисса равна $ \displaystyle 2$.

Ответ: $ \displaystyle 2$

Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.

1. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты $ \displaystyle \left( 8;

2. Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты \( \displaystyle \left( 8;

3. Какого радиуса должна быть окружность с центром в точке \( \displaystyle P\left( 8;

6 \right),$ чтобы она касалась оси абсцисс?

4. Найдите ординату точки пересечения оси $ \displaystyle Oy$ и отрезка, соединяющего точки $ \displaystyle A\left( 6;\text< >8 \right)$ и $ \displaystyle B\left( -6;\text< >0 \right).$

$ \displaystyle 5$;

$ \displaystyle 3$;

$ \displaystyle 6$;

$ \displaystyle 4$.

Умножение векторов

Все удалось? Очень на это надеюсь! Теперь – последний рывок.

Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат, но также встречается повсеместно и в задачах повышенной сложности.

Какое из своих обещаний я еще не сдержал?

Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл?

Забыл! Забыл объяснить, что значит умножение векторов.

Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:

Скалярное произведение (результат – число);

Векторное произведение (результат – вектор).

Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим чуть позже. А пока мы остановимся на скалярном произведении.

Есть аж два способа, позволяющих нам его вычислить:

Через координаты векторов;

Через длины векторов и угол между ними.

Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:

Источник

Читайте также: Что значит смена времени года это