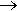Что значит все корни левые

Что означает, если на рентгене корни легких расширены

Туберкулез – одно из самых страшных заболеваний, которое ежегодно уносит тысячи человеческих жизней по всему земному шару. Не зря прохождение флюорографии обязательный пункт в прохождении медицинского осмотра, ведь именно с ее помощью болезнь можно диагностировать на ранней стадии. Если раньше туберкулез поражал только бездомных людей, которые живут впроголодь, то теперь все чаще им болеет вполне обеспеченные и респектабельнее граждане.

Осмотр рентгеновского снимка

Социальное положение не является лекарством от всех болезней, поэтому не стоит игнорировать прохождение флюорографии. Однако, зачастую получив на руки заключение врача — рентгенолога, мы не можем разобраться, что там написано. Поэтому важно иметь базовые знания о рентгенологии, чтобы не впадать преждевременно в панику.

Общая информация о флюорографии и какие проблемы выявляет

Рентген – один из самых дешевых и простых способов обнаружить заболевания в грудной клетке. Плотности органов может сказать о многом, отклонения от нормы чаще всего являются первым симптомом болезни. Соединительная ткань в легких отличается высокой прочностью, она постоянно развивается. От того, каким способом это происходит и в каких местах она скапливается, можно определить начало той или иной проблемы.

Человек, страдающий от астмы или бронхита, увидит на рентгеновском снимке уплотненные стенки сосудов и бронхов. Полости в легких также имеют свой уникальный вид, особенно в тех случаях, когда наполняются жидкостью. Расширенные и уплотненные корни легких быстро сможет обнаружить только опытный рентгенолог.

Флюорография может вывить такие патологии, как:

• Наличие новообразований;
• Чужеродные тела во внутренних органах;
• Уплотнения;
• Воспаления.

Если после прохождения медицинского осмотра вам спокойно выдали на руки медкнижку и отправили домой, значит у вас все в порядке со здоровьем. При обнаружении каких-либо отклонений медицинский работник обязан вас о них уведомить и направить на дополнительное обследование.

Расширенные корни легких

Структуры, расположенные на «входе» в легочную систему называются корнями, из них образуются лимфоузлы, сосуды и т.п. Чаще всего корни легких уплотнены и расширены одновременно. Если обнаружено только локальное уплотнение, оно символизирует о наличии хронической болезни и образуется в результате скопления значительного количества соединительной ткани.

Расширенный корень правового (левого) легкого образуется в результате отечности больших сосудов и бронхов, либо при увеличении лимфатических узлов. Уплотнение в совокупности с расширением может иметь обособленный или одновременный характер, причиной такого «комплексного» отклонения становится пневмония или острый бронхит. Подобное явление наблюдается и при других болезнях, но там оно сопровождается очагами воспалениями, полостями и т.д. В этих случаях корни правого (левого) легкого расширены по причине увеличения локальной категории группы лимфатических узлов.

Тяжистые корни

Если в полученном медицинском заключении указано, что корни в легких расширенные и имеют уплотнения, то скорей всего у вас в организме идут воспалительные процессы или «зарождается» бронхит. Такие симптомы чаще всего характерны для людей, страдающих от такой пагубной привычки, как курение. Поскольку дым и табачная смола, попадающая в легкие и бронхи, постоянно их раздражает, как итог происходит уплотнение стенок лимфатических узлов, отвечающих за «уборку» в легких. При этом дискомфортных ощущений у курильщика нет.

Это важно! Если вы чувствуете недомогание, стоит обратиться к участковому терапевту. Да, хронические болезни не становятся препятствием для нормальной жизнедеятельности, но и забывать о них не стоит. Сами по себе они не могут привести к летальному исходу, зато становятся явными вестниками приближающихся смертельных заболеваний.

Фиброз

Четкое проявление фиброзной ткани на рентгеновском снимке – это результат перенесенных заболеваний легких. Ее основное предназначение – заполнить «пустое место» в организме. Если у вас проникающая рана в грудной клетке или вы перенесли хирургическое вмешательство, то фиброзная ткань берет на себя функции соединительной и заполняет образовавшуюся пустоту.

Фиброз – это скорей положительный диагноз, его причиной становится потеря части легочной ткани. Негативных последствий он не несет.

Усиленный легочный рисунок

Помимо расширения и уплотнения корней, симптомом различных острых заболеваний является усиление легочного рисунка. Причиной становится интенсивное снабжение кровью некоторых участков. Любой островоспалительный процесс в организме приводит к изменению рисунка. При пневмонии пациента направляют на повторный рентген, чтобы убедиться в отсутствии пневмонита. На снимках эти заболевания выглядят практически идентично. После того, как воспаление устранено, легочный рисунок приходит в норму примерно через четырнадцать дней.

Флюорография в России далека от идеала, но она выявляет такие опасные заболевания, как рак или туберкулез. В обязательном порядке ее нужно проходить не менее одного раза в пару лет, поскольку у нас в стране идеальные эпидемиологические условия для распространения туберкулеза. Каждый человек априори находится в группе риска. Рентген – это возможность защитить себя от смертельного заболевания, поскольку если его выявить на начальной стадии, гораздо больше шансов сохранить жизнь.

Источник

Алгебраические критерии устойчивости

1. Понятие устойчивости системы

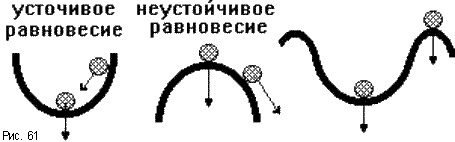
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис.61). Говорят, что система устойчива «в малом», если определен факт наличия устойчивости, но не определены ее границы. Система устойчива «в большом», когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

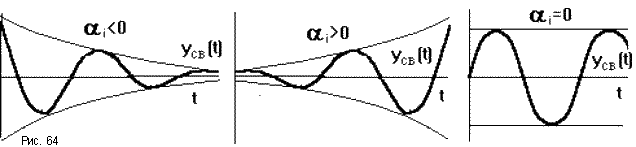
В соответствии с классическим методом решение дифференциального уравнения ищется в виде:

Здесь yсв(t) — общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью:

Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y_вын(t) — частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется вынужденный. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р. После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей y_вын = y(t ). Если внешнее воздействие само будет изменяться по синусоидальному закону P = P _o sin(t + ), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть y_вын = y _max sin(t + y).

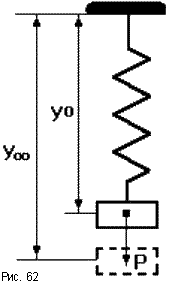
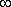
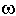
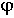
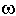
Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t . Свободная составляющая представляет собой сумму из n отдельных составляющих: , где p _i корни характеристического уравнения D(p) = a ₀ p _n + a ₁ p _n -1 + a ₂ p _n -2 + . + a _n = 0. Корни могут быть либо вещественными p _i = a _i , либо попарно комплексно сопряженными p _i = a _i ± ji. Постоянные интегрирования А _i определяются исходя из начальных и конечных условий, подставляя в общее решение значения u, y и их производные в моменты времени t = 0 и t .

Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y_св(t) _i , каждому положительному — экспоненциально расходящаяся, каждому нулевому корню соответствует y_св(t) _i = const (рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой _i , при положительной вещественной части — расходящиеся колебания, при нулевой — незатухающие (рис.64).

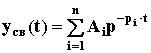
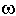
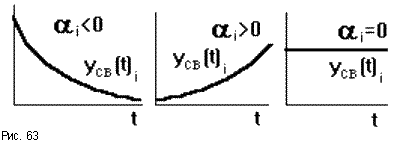
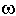
Так как после снятия возмущения y_вын(t) = 0, то устойчивость системы определяется только характером свободной составляющей y_св(t). zПоэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.

Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми, с положительными — правыми (рис.65).

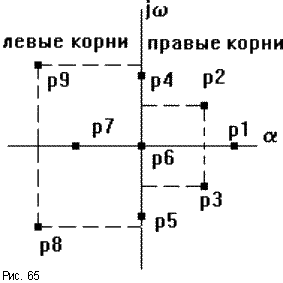
Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a _n = 0), а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости.

Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).

8.2. Алгебраические критерии устойчивости

8.2.1. Необходимое условие устойчивости

Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде

где p ₁ , p ₂ , . p _n — корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней

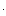
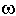
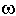
отрицательны, что можно записать как a _i = -|a _i | ₀ (p + |a ₁ |)(p + |a ₂ | — j2)(p + |a ₂ | + j2). = 0.

Перемножая комплексно сопряженные выражения, получим:

a ₀ (p + |a ₁ |)((p + |a ₂ |)2 + (2)2). = 0.

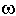
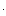
После раскрытия скобок должно получиться выражение

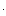
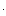
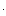
a ₀ p n + a ₁ p n-1 + a ₂ p n-2 + . + a _n = 0.

Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a ₀ ,a ₁ . a _n не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a ₀ > 0, a ₁ > 0, . , a _n > 0. В дальнейшем будем рассматривать только уравнения, где a ₀ > 0. В противном случае уравнение домножается на -1.

Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.

8.2.1. Критерий Рауса

Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке — с нечетными;

3) остальные элементы таблицы определяется по формуле: c _k,i = c _{k+ 1,i — 2} — ric _{k + 1,i — 1} , где ri = c _{1,i — 2} /c _{1,i — 1} , i 3 — номер строки, k — номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.

Источник