- Вращательное движение
- Содержание
- Характеристики вращения тела
- Кинематические характеристики
- Динамические характеристики
- См. также
- Ссылки
- Полезное
- Смотреть что такое «Вращательное движение» в других словарях:
- Вращательное движение
- Связанные понятия
- Упоминания в литературе
- Связанные понятия (продолжение)
- Вращательное движение тела в физике — виды, формулы и определения с примерами
- Движение точки по окружности
- Вращение твердого тела
- Динамика вращательного движения
- Пример
- Кинематика вращательного движения
Вращательное движение
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам.
Содержание
Характеристики вращения тела
Кинематические характеристики
Вращение твердого тела, как целого характеризуется углом 


При равномерном вращении (T оборотов в секунду),
- Частота вращения — число оборотов тела в единицу времени.

- Период вращения — время одного полного оборота. Период вращения T и его частота
связаны соотношением
.
- Линейная скорость точки, находящейся на расстоянии R от оси вращения

- Угловая скорость вращения тела

Динамические характеристики
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергии вращения можно записать в виде 

- Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех nматериальных точек системы на квадраты их расстояний до оси:

где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Кинетическая энергия вращательного движения
где Iz — момент инерции тела относительно оси вращения. 
См. также
Ссылки
- http://physics.ru/courses/op25part1/content/chapter1/section/paragraph23/theory.html
- Б. Яворский А. Детлаф, Физика, М.: Дрофа, 1998.
- Джанибеков демонстрирует пример вращения абсолютно жесткого тела, закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции
- Вращение твёрдых тел в невесомости вокруг разных осей
| Wikimedia Foundation . 2010 . ПолезноеСмотреть что такое «Вращательное движение» в других словарях:ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ — твёрдого тела, 1) В. д. вокруг ос и движение тв. тела, при к ром к. л. две его точки А и В остаются всё время неподвижными (рис.). Прямая АВ, проходящая через эти точки, наз. осью вращения; все точки тела при В. д. описывают окружности в… … Физическая энциклопедия ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ — твердого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси. 2) Вокруг точки движение тела, при котором одна его точка О неподвижна, а все… … Современная энциклопедия ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ — твердого тела . 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси;2)] вокруг точки движение тела, при котором одна его точка О неподвижна, а все … Большой Энциклопедический словарь Вращательное движение — твердого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси. 2) Вокруг точки движение тела, при котором одна его точка О неподвижна, а все… … Иллюстрированный энциклопедический словарь вращательное движение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN rotary motionrotational motion … Справочник технического переводчика Вращательное движение — твёрдого тела, 1) вращательное движение вокруг оси движение твёрдого тела, при котором какие нибудь две его точки А. и В остаются всё время неподвижными (см. рис.). Прямая AB, проходящая через эти точки, называется осью вращения; все… … Большая советская энциклопедия вращательное движение — твёрдого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси; 2) вокруг точки движение тела, при котором одна его точка О неподвижна, а все … Энциклопедический словарь вращательное движение — sukamasis judesys statusas T sritis automatika atitikmenys: angl. rotary motion; rotary movement vok. Drehbewegung, f; Rotation, f; Rotationsbewegung, f; umlaufende Bewegung, f rus. вращательное движение, n pranc. mouvement de rotation, m;… … Automatikos terminų žodynas вращательное движение — sukamasis judėjimas statusas T sritis fizika atitikmenys: angl. rotary motion; rotational motion vok. Drehbewegung, f; Rotationsbewegung, f rus. вращательное движение, n pranc. mouvement de rotation, m; mouvement rotatoire, m … Fizikos terminų žodynas вращательное движение — sukamasis judesys statusas T sritis Kūno kultūra ir sportas apibrėžtis Judesys, vykstantis (atliekamas) kūnui ar jo dalims sukantis apie tašką arba ašį. Viso kūno sukamasis judesys vyksta apie ašį, kuri gali būti kūno viduje arba už kūno. Tokių… … Sporto terminų žodynas Источник Вращательное движение
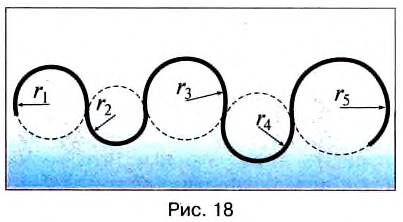
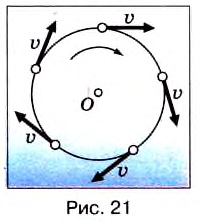
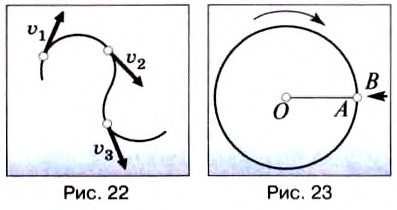
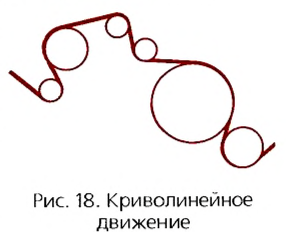
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым. Связанные понятияУпоминания в литературеСвязанные понятия (продолжение)Простейшие механизмы — устройства, служащие для преобразования направления и величины (модуля) силы. Представляют собой элементы более сложных механизмов. Некоторые из простейших механизмов появились в глубокой древности. Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО). В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу; это энергия движения и сопровождающего его взаимодействия. Источник Вращательное движение тела в физике — виды, формулы и определения с примерамиСодержание: Вращательное движение тела: До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18). Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности. Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности. Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги где Направление скорости проще всего определить на опыте. Опыт: К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20). Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом. Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22). Опыт: Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени. Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями. Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения. Период обращения — это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Обозначается период обращения большой латинской буквой Т. Если за время Единицей периода обращения в СИ является одна секунда (1 с). Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с. Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности Обозначается частота обращения малой латинской буквой * В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой Если за время Единицей частоты обращения в СИ является единица, разделённая на секунду Движение точки по окружностиДвижения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным. Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться. Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время где Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки — длина дуги окружности АВ — равна длине радиуса R. Единицей угловой скорости является радиан в секунду (рад/с). 1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад. При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с). Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения. Период вращения (Т) — это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения: где t — время вращения, N — количество выполненных оборотов. Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота): где N — количество совершенных оборотов за время t . Частота вращения измеряется в оборотах за секунду (об/с). Частота вращения Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой Таким образом, длина окружности За один оборот материальная точка осуществляет угловое перемещение 2 Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь Вращение твердого телаТвердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет. Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры. В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких? Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения. Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния — чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т — время одного полного вращения; вращательная частота (частота вращения) Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам. Динамика вращательного движенияПри просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен. Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении. По третьему закону Ньютона: и при вращении появляется также центробежная сила. На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет: Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения. ПримерПри движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки Чтобы тело не упало из точки Кинематика вращательного движенияПри криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке. Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление. Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них. Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота
По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению
Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения
Единица угловой скорости в СИ — радиан в секунду При движении по окружности с постоянной по модулю скоростью v угловая скорость Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:
При совершении полного оборота
Проекции скорости
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным Нормальное ускорение Как и при прямолинейном равноускоренном движении, ускорение
Модуль полного ускорения находится по теореме Пифагора:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. Источник |

 связаны соотношением
связаны соотношением  .
.

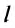
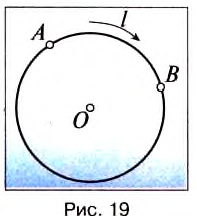
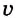 — скорость движения тела по окружности;
— скорость движения тела по окружности; 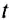 — время движения тела.
— время движения тела.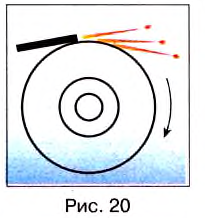
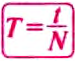
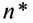 .
.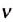 (ню).
(ню). материальная точка совершила N оборотов, то, чтобы определить частоту обращения
материальная точка совершила N оборотов, то, чтобы определить частоту обращения 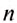 , нужно N поделить на
, нужно N поделить на 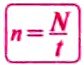 а так как
а так как  .
. 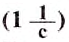 .
. 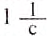 это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду
это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду 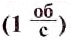 , часто применяют также единицу один оборот в минуту
, часто применяют также единицу один оборот в минуту 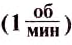 .
.
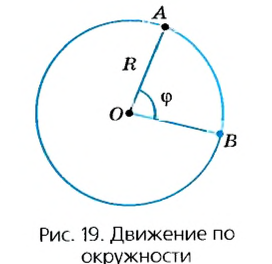
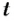 переходит из точки А в точку В. При этом отрезок OA поворачивается на угол
переходит из точки А в точку В. При этом отрезок OA поворачивается на угол  — угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:
— угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:
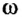 (греческая буква «омега») — угловая скорость;
(греческая буква «омега») — угловая скорость; 

 определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.
определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.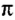 («пи»).
(«пи»).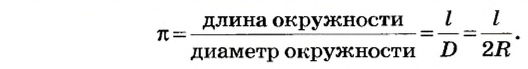
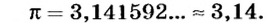
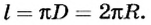
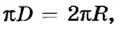 то линейная скорость равномерного движения точки по окружности
то линейная скорость равномерного движения точки по окружности 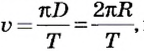 или
или 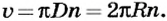
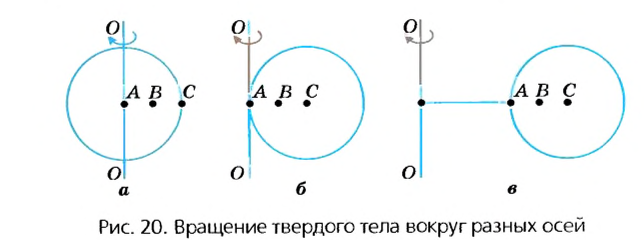
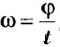 для всех точек данного тела также будет одинаковой.
для всех точек данного тела также будет одинаковой.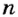 — количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.
— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.
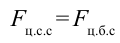
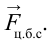
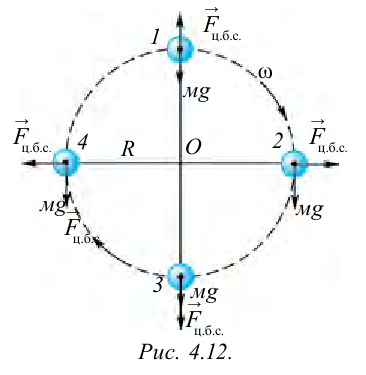
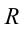 . В точке 1, из-за того что центробежная сила
. В точке 1, из-за того что центробежная сила 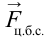 направлена противоположно силе тяжести
направлена противоположно силе тяжести 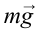 , вес тела уменьшается:
, вес тела уменьшается: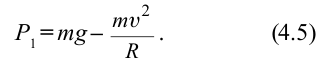


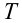 . Скорость тела в точке
. Скорость тела в точке 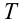 равна 30 м/с.
равна 30 м/с. 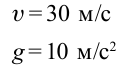
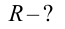
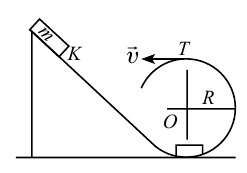
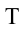 должно
должно 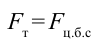 выполняться следующее условие:
выполняться следующее условие: 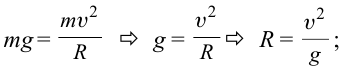
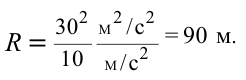
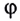 (рис. 25)
(рис. 25)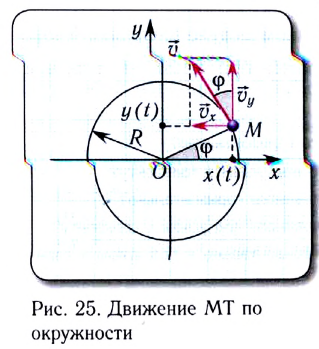

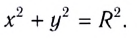
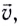 с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).
с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).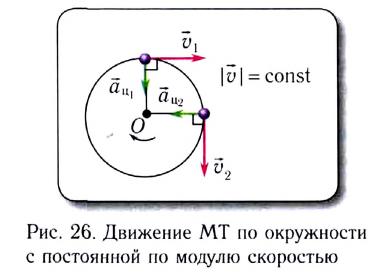
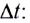
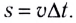
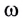 — это отношение угла поворота
— это отношение угла поворота 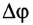 к промежутку времени
к промежутку времени 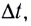 за который этот поворот произошел:
за который этот поворот произошел: 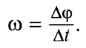
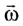 со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).
со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).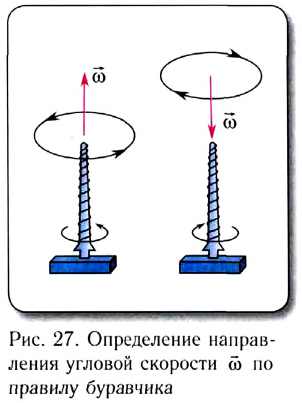
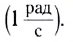
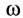 является величиной постоянной и ее модуль равен отношению угла поворота
является величиной постоянной и ее модуль равен отношению угла поворота 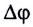 к промежутку времени
к промежутку времени 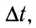 за который этот поворот произошел:
за который этот поворот произошел: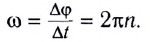
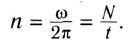
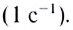 Время совершения одного оборота называется периодом вращения Т.
Время совершения одного оборота называется периодом вращения Т.
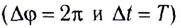 период определяется по формуле
период определяется по формуле

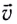 (см. рис. 25) с течением времени изменяются по закону
(см. рис. 25) с течением времени изменяются по закону 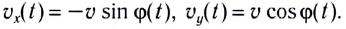
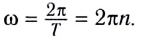

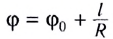 (докажите самостоятельно), где
(докажите самостоятельно), где 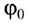 — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид
— угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид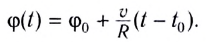
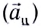 или нормальным
или нормальным 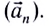 Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости
Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости 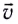 с течением (см. рис. 26). Его модуль определяется формулой
с течением (см. рис. 26). Его модуль определяется формулой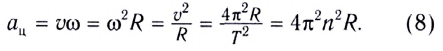
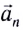 в любой момент времени перпендикулярно скорости
в любой момент времени перпендикулярно скорости 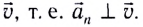
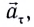 называемое тангенциальным (касательным), совпадает с направлением скорости
называемое тангенциальным (касательным), совпадает с направлением скорости 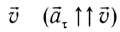 или направлено противоположно ей
или направлено противоположно ей 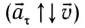 и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение
и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 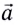 можно представить в виде векторной суммы нормального ускорения
можно представить в виде векторной суммы нормального ускорения 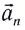 и тангенциального ускорения
и тангенциального ускорения 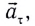 направленного по касательной к окружности в данной точке (рис. 28):
направленного по касательной к окружности в данной точке (рис. 28): 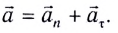
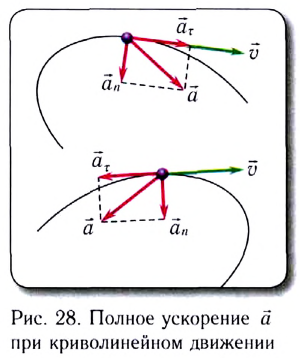
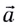 всегда направлено в сторону вогнутости траектории (см. рис. 28).
всегда направлено в сторону вогнутости траектории (см. рис. 28).
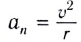 — нормальное ускорение, с которым точка двигалась бы по дуге
— нормальное ускорение, с которым точка двигалась бы по дуге 

