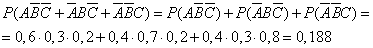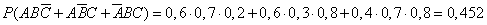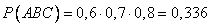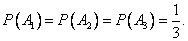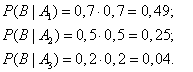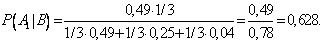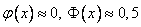- Теория вероятности и комбинаторика
- ХОД УРОКА:
- 1. Вступительное слово учителя.
- 2. Изучение нового материала.
- 3.Закрипление материала.
- Итог урока.
- Теория вероятностей, формулы и примеры
- Основные понятия
- Формулы по теории вероятности
- Случайные события. Основные формулы комбинаторики
- Классическое определение вероятности
- Геометрическое определение вероятности
- Сложение и умножение вероятностей
- Формула полной вероятности и формула Байеса
- Формула Бернулли
- Наивероятнейшее число успехов
- Формула Пуассона
- Теоремы Муавра-Лапласа
Теория вероятности и комбинаторика
Разделы: Математика
ТИП УРОКА: изучение нового материала.
ЦЕЛЬ: создать условия для осознания и осмысления блока новой учебной информации.
- Способствовать запоминанию основной терминологии, умению устанавливать события вероятности и вычислять перестановки и размещения;
- Способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни
- Способствовать воспитанию аккуратности;
НОВЫЕ ПОНЯТИЯ: достоверные события, случайные
ОБОРУДОВАНИЕ: доска, презентация
- Орг.момент – 1 мин.
- Актуализация – 5 мин.
- Мотивация – 2 мин.
- Объяснение нового материала – 5 мин.
- Первичное осмысление и закрепление – 15 мин.
- Решение задач – 10 мин.
- Подведение итогов – 2 мин.
ХОД УРОКА:
1. Вступительное слово учителя.
Вы, наверное, не раз слышали или сами говорили “это возможно”, “это не возможно”, это обязательно случиться”, “это маловероятно”
Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти
Случай , случайность – сними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная ошибка. Этот ряд можно продолжать до бесконечности. Казалось бы, тут нет места для математики – какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности – они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями
Слово “событие” в быту применяют к значительным явлениям ( день рождение, экзамен, свадьба), а в математике – ко всем возможным исходам рассматриваемой ситуации например при бросание игральной кости событие- это выпадение той или иной грани.
2. Изучение нового материала.
События будем обозначать большими латинским буквами А,В,С. вероятность произвольного события (Х) будем обозначать через Р(Х).
События, которые при данных условиях обязательно происходят, называют достоверными (смена дня и ночи) события, которые при данных условиях не могут произойти, называют невозможными события, которые при данных условиях иногда происходят, а иногда не происходят, называются возможными или случайными. События, возможности наступления которых одинаковы называются равновозможными или равновероятными (подкидывание монеты)
Какие из следующих событий – случайные, достоверные, невозможные:
Для каждого из перечисленных событий определите, какое оно: достоверное, возможное, невозможное
8–10 придумайте и запишите в тетрадь события, чтобы они соответствовали знакам в таблице например, событие 8 должно быть очень вероятным.
Достоверное
Возможное
невозможное
ВПЕРВЫЕ ВЕРОЯТНОСТЬ СЛУЧАЙНЫХ СОБЫТИЙ В играх вычислили в XVII в. французские математики Блез Паскаль и Пьер Ферма. Они подсчитали число шансов события из общего возможного числа равновероятных исходов. Давайте проследим за их рассуждениями.
Исход какого либо испытания, опыта или игры выражающийся в событии А, назовем шансом события А. Например, при бросании игральной кости возможно 6 равновероятных исходов А1, А2, А3, А4, А5, А6. – выпадение 1,2,3,4,5,6. пусть событие А (выпадение четного числа очков т.е.2,4,6) в этом случае Р(А)=

Если при каких –либо условиях имеются m равновероятных исходов и из них m приводят к событию А, то вероятность события А равна отношению m n
Пример 1: хорошо перетусуем колоду карт случайно вынем 1 карту. Событие А(вытянута карта червонной масти) и В (вытянут туз) из 36 исходов имеются соответственно 9 и 4 шансов. Поэтому Р(А)=
Пример 2: на экзамене -24 билета. Андрей не разобрался в одном билете и очень биться его вытянуть. Какова вероятность. Что Андрею достанется несчастный билет?
А — достанется несчастливый билет: Исходов -24; Шансы =1, тогда Р(А)=
Пример 3: в лотереи 10 выигрышных билетов и240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?
А — выиграть: Исходов всего 240+10=250; Шансы=10; Р(А)=
Пример 4: в лотереи 100 билетов, из них 5 выигрышных. Какова вероятность проигрыша?
А — проиграть: Исходов 100; Шанс =100-5=95, тогда Р(А)=
В ящике лежат 8 красных,2 синих, 20 зеленых карандашей. Вы наугад вынимаете карандаш. Какова вероятность того, что это красный карандаш? желтый карандаш? Не зеленый карандаш? Какое количество карандашей нужно вытянуть, чтобы с вероятностью, равной 1, среди них был зеленый карандаш?
А — вытянут красный карандаш: Исходов 20+8+2=30;Шансов 8;Р(А)=
В — желтый карандаш: Исходов 30; Шансов 0; Р(В)=0
С — не зеленый карандаш: Шансов 30; Исходов 30-20=10; Р(С)=
А теперь давайте вспомним знаменитую басню Крылова “Квартет” “проказница Мартышка, Осел, Козел да косолапый мишка” устроили любопытный эксперимент: они исследовали влияние взаимного расположения на качество исполнения. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты. Зададим вопрос : сколько существует способов, чтобы рассадить, например в один ряд, четырех музыкантов?
Еще одна ситуация: нас приглашают на некий конкурс с 8 участницами. Одновременно проводиться викторина: нужно угадать, кто займет в конкурсе 1,2,3 место. Сколько всего существует вариантов?
Общее у этих двух задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. Особая примета комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался со слов “Сколькими способами ?
Давайте рассмотрим первую задачу:
Давайте расставим наших участников квартета в ряд, такое упорядоченное положение назовем перестановкой. Попытаемся ответить на вопрос сколько всего возможных перестановок ? число перестановок обозначим Рп, где п — количество объектов( в нашем случае это будет 4) сначала возьмем п=1 ( Мартышку) – имеется 1 способ
П=2 ( мартышка, Осел) – имеется 2 перестановки Р2 = Р1*2 =1*2, добавим теперь Козла, к каждой из перестановок дух объектов можно пристроить третий, тремя различными способами: спереди, сзади, посередине отсюда Р3 = Р2 *3=2*3=6 , и добавим нашего косолапого Мишку Р4= Р3 *4=1*2*3*4=24. значит способов “усесться чинно в ряд” существует 24. давайте запишем общую формулу: Рп =1*2*3*4….*п=п! восклицательным знаком( в математике он называется факториалом) принято обозначать произведение всех натуральных чисел от 1 до п, мы не просто вывили формулу, но одновременно указали способ, как получить все возможные перестановки. Надо отметить, что этот способ далеко не единственный. 0!=1
Давайте попробуем решить задачу про участниц.
Нам в этой задаче нужно отобрать из имеющихся объектов n= 8, произвольное m=3 штук(m Каждое такое упорядоченное расположение называется размещением . Сколько существует размещений при заданных n,m. Ответ на этот вопрос мы дадим основываясь на знание перестановок(задача про квартет)
Обозначим искомое число Аn m . Сначала возьмем любую перестановку всех n(8) объектов и рассмотрим первые m(3) из них. Они образуют размещение m(3) объектов из n(8) имеющихся, тогда как последние n-m(8-3=5) объектов могут быть переставлены Р5 способами. Значит каждому способу можно “пришить” Р5, что порождает столько же перестановок всех n объектов Рn= Аn m * Рn-m отсюда Аn m =
3.Закрипление материала.
1.У нас есть 9 разных книг из серии “Занимательная математика”. Сколькими способами можно:
- Расставить их на полке.
- Подарить три из них победителям школьной олимпиады, занявшим первые три места.
2.Сколькими способами 5 человек могут встать в очередь к билетной кассе.
3.В чемпионате России по футболу участвуют 16 команд. Сколькими способами могут распределиться три призовых места.
1. В 10-м классе изучается 14 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день 7 уроков и все разные. Как называется такая комбинация в комбинаторике.
2. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? Как называется такая комбинация в комбинаторике.
1. На книжную полку влезает только 5 книг из 8. Сколькими способами можно заполнить этими книгами такую полку. Как называется такая комбинация в комбинаторике.
2. В магазине имеется четыре типа диванных подушек: круглые, овальные, прямоугольные и треугольные. Сколькими способами можно расставить их в ряд. Как называется такая комбинация в комбинаторике.
Итог урока.
Домашнее задание: Составить по 2 задачи на вероятность, перестановку и размещение.
Источник
Теория вероятностей, формулы и примеры
О чем эта статья:
Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.
Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.
Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».
Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.
Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.
Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:
- Дискретная случайная величина — величина, которая в результате испытания может принимать определенные значения с определенной вероятностью, то есть образовывать счетное множество.
Элементы множества можно пронумеровать. Они могут быть как конечными, так и бесконечными. Например: количество выстрелов до первого попадания в цель.
Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.
Вероятностное пространство — это тройка (Ω, Σ, Ρ) иногда обрамленная угловыми скобками: ⟨ , ⟩ , где
- Ω — это множество объектов, которые называют элементарными событиями, исходами или точками.
- Σ — сигма-алгебра подмножеств , называемых случайными событиями;
- Ρ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .
Формулы по теории вероятности
Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.
Случайные события. Основные формулы комбинаторики
Классическое определение вероятности
Вероятностью события A в некотором испытании называют отношение:
P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A
- Вероятность достоверного события равна единице.
- Вероятность невозможного события равна нулю.
- Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Таким образом, вероятность любого события удовлетворяет двойному неравенству:
- 0 ≤ P(A) ≤ 1.
Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?
Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:
Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.
Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?
Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).
Геометрическое определение вероятности
Геометрическая вероятность события А определяется отношением:
P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно
Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.
Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?
- A — встреча с другом состоится, х и у — время прихода. Значит:
0 ≤ х, у ≤ 60. - В прямоугольной системе координат этому условию удовлетворяют точки, которые лежат внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть:
x−y y.
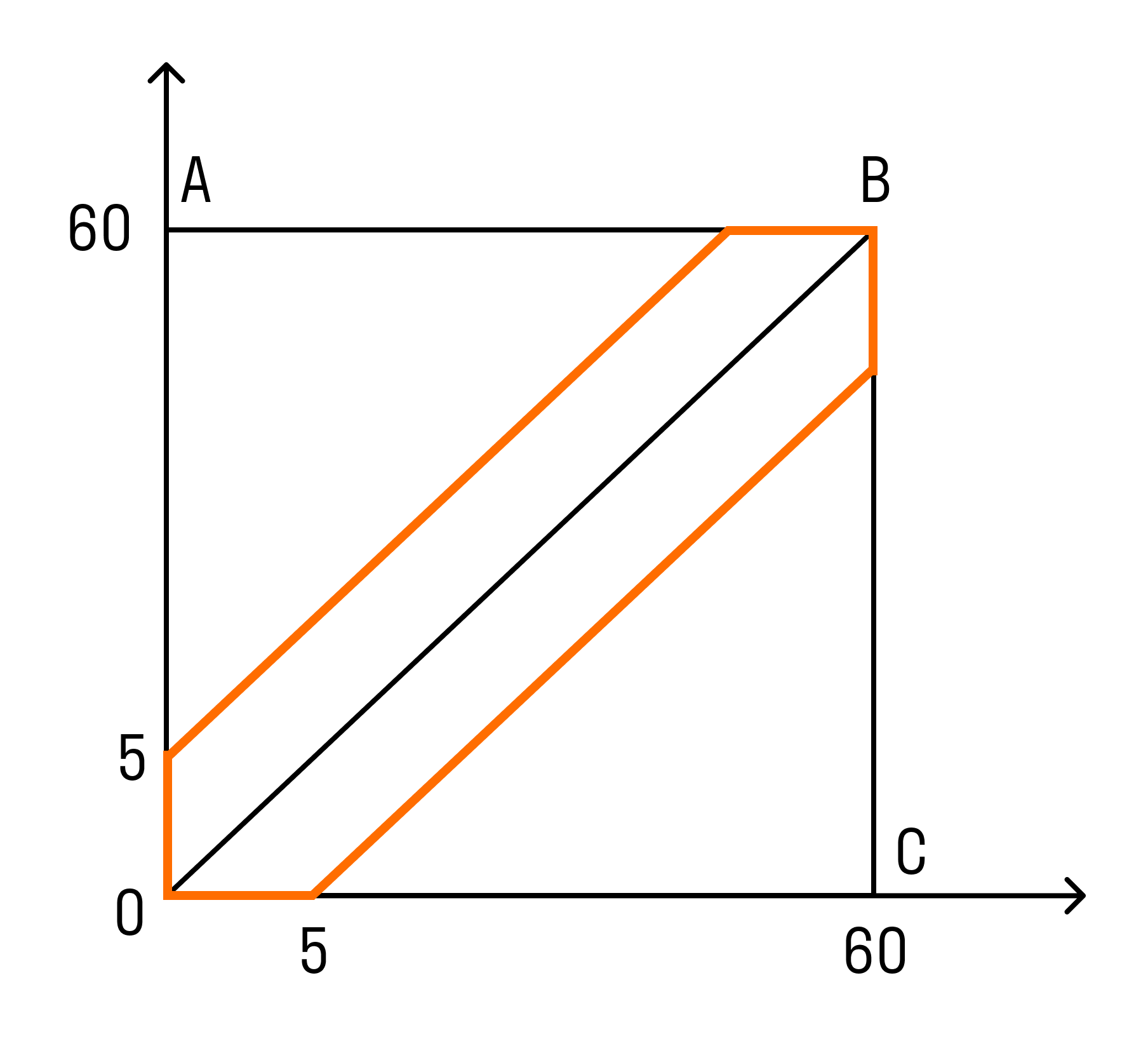
P(A)=SG/SOABC= 60 * 60 — 55 * 5560 * 60 = 23144 = 0,16
У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!
Сложение и умножение вероятностей
- Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
- События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
- Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B)
Эта теорема справедлива для любого числа несовместных событий:
Если случайные события A1, A2. An образуют полную группу несовместных событий, то справедливо равенство:
- P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:
P(A + B) = P(A) + P(B) − P(AB)
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:
P(AB) = P(A) * P(B)
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.
Найдем вероятности того, что формула содержится:
- только в одном справочнике;
- только в двух справочниках;
- во всех трех справочниках.
А — формула содержится в первом справочнике;
В — формула содержится во втором справочнике;
С — формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.
Формула полной вероятности и формула Байеса
Если событие А может произойти только при выполнении одного из событий B1, B2, . Bn, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:
 |
Вновь рассмотрим полную группу несовместных событий B1, B2, . Bn, вероятности появления которых P(B1), P(B2), . P(Bn). Событие А может произойти только вместе с каким-либо из событий B1, B2, . Bn, которые называются гипотезами. Тогда по формуле полной вероятности: если событие А произошло — это может изменить вероятности гипотез P(B1), P(B2), . P(Bn).
По теореме умножения вероятностей:
Аналогично, для остальных гипотез:
Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.
Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
- Возможны три гипотезы:
- А1 — на линию огня вызван первый стрелок,
- А2 — на линию огня вызван второй стрелок,
- А3 — на линию огня вызван третий стрелок.
- Так как вызов на линию огня любого стрелка равно возможен, то
- В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при наших гипотезах равны:
- По формуле Байеса находим вероятность гипотезы А1 после опыта:
Формула Бернулли
При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
- Бросаем игральный кубик, где вероятности выпадения определенной цифры одинаковы в каждом броске.
- Включаем лампы с заранее заданной одинаковой вероятностью выхода из строя каждой.
- Лучник повторяет выстрелы по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой.
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.
- Обозначим вероятность появления события А в единичном испытании буквой р, значит:
p = P(A), а вероятность противоположного события (событие А не наступило) — буквой q
q = P(¯A) = 1 — p.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли:
Pn(k) = Cn k * p k * q n-k , где q = 1 — p.
Биномиальное распределение — распределение числа успехов (появлений события).
Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.
Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:
Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂
Наивероятнейшее число успехов
Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:
np — q ≤ k ≤ np + p, где q=1−p
Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.
Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.
- По условию дано: n = 730, p = 1/365, g = 364/365
- np — g = 366/365
- np + p = 731/365
- 366/365 ≤ m ≤ 731/365
- m = 2
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.
В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:
 |
Здесь λ = np обозначает среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.
События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).
При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.
Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
- По условию дано: n = 1000, p = 0,002, λ = np = 2, k = 3.
- Искомая вероятность после подстановки в формулу:
P1000(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.
Ответ: ориентировочно 0,18.
Теоремы Муавра-Лапласа
Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью p, q = 1 — p (условия схемы Бернулли). Обозначим как и раньше, через Pn(k) вероятность ровно k появлений события А в n испытаниях.
Кроме того, пусть Pn(k1;k2) — вероятность того, что число появлений события А находится между k1 и k2.
Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:
- при больших x верно
Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.
Источник