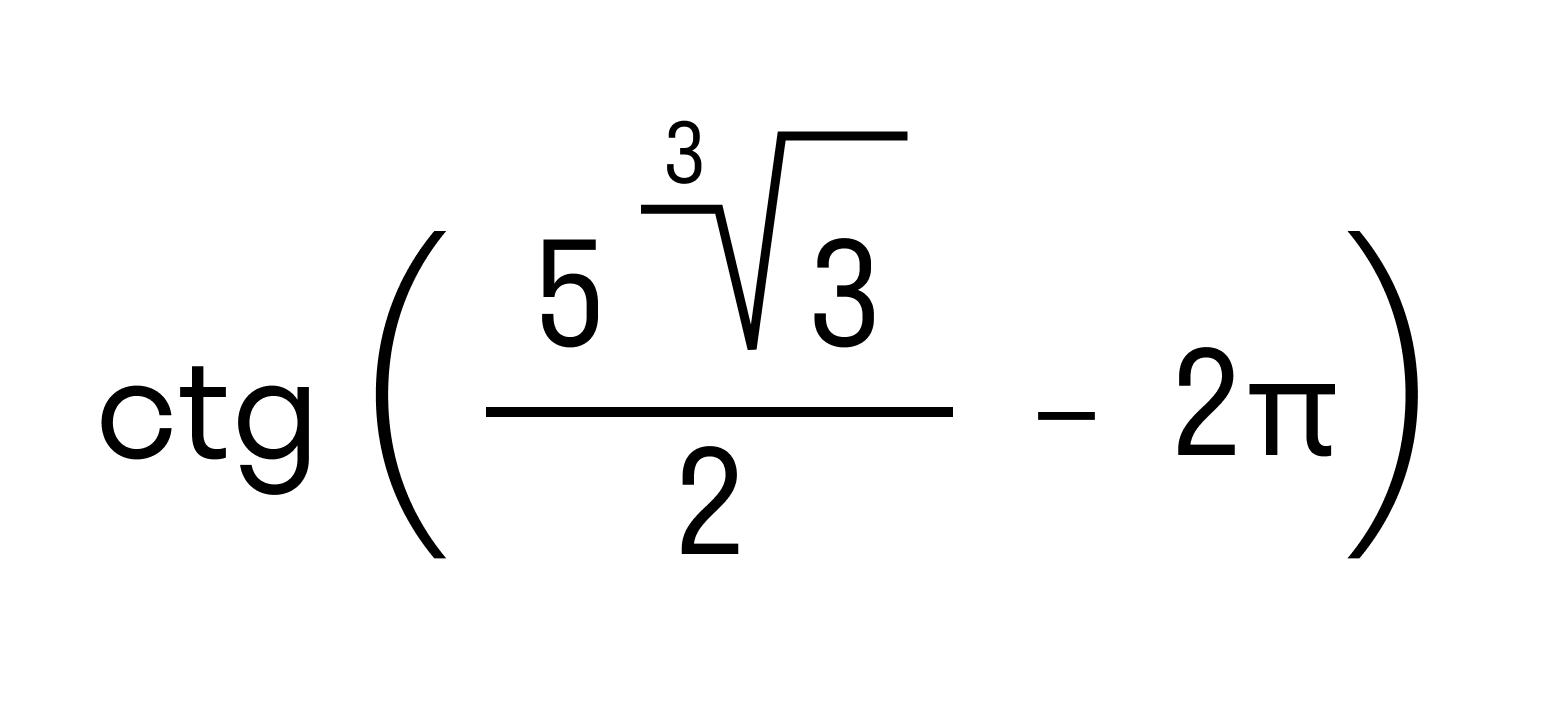Что значит вещественное число пример

Действительные числа

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

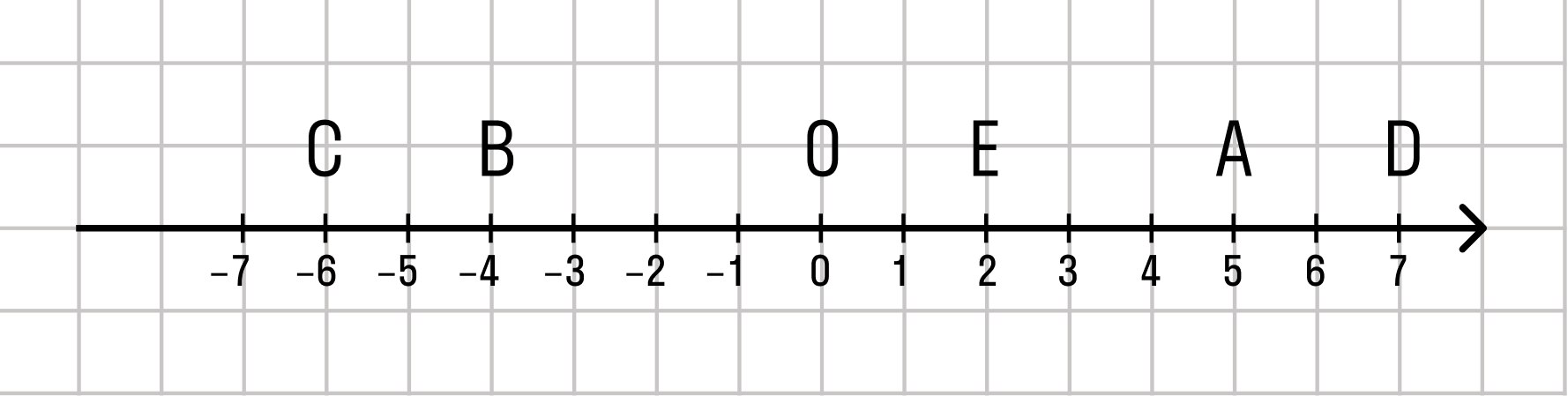
Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Представления действительных чисел

По определению действительными числами являются:

• любое натуральное число;
• любое целое число;
• любая обыкновенная дробь (как положительная, так и отрицательная);
• любое смешанное число;
• любая десятичная дробь (положительная, отрицательная, конечная, бесконечная периодическая, бесконечная непериодическая).

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

На множестве R действительных чисел справедливы формулы сокращенного умножения и привычные нам законы. Например: a^2 — b^2 = (a — b)(a + b) — это было справедливо на множестве рациональных чисел, но все это справедливо и на множестве действительных чисел.

• a + b = b + a; ab = ba — теперь все эти законы справедливы на множестве действительных чисел.

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

1. Из двух действительных чисел a и b большим считается то, которое расположено правее на координатной прямой. Например:
2. √3 > √2; -3 > -5
3. Число a считается больше числа b, если разность a — b > 0.

Аналогично a меньше b тогда и только тогда, когда разность a — b a — b a — b 2, 6 — 2 = 4 > 0

Источник

2.6. Вещественные числа¶

Вещественные, или действительные, числа — это, грубо говоря, и целые и дробные. Они, конечно, нередко возникают в задачах, но при работе с ними возникают серьезные проблемы, которые не в каждой книге по программированию будут описаны.

На самом деле эта тема неожиданно сложная. Постарайтесь понять всё, что написано в этом разделе, но если что-то не поймете по началу, это не страшно. Главное — два правила работы с вещественными числами, которые я напишу ниже.

2.6.1. Запись чисел с плавающей точкой¶

Вы точно знаете, что вещественные числа можно записывать в виде «12.34» — это «двенадцать целых тридцать четыре сотых».

Иногда вместо точки используется запятая, но даже в обычной жизни сейчас, кажется, чаще используют точку, а уж в программировании и подавно почти всегда используется точка. Вообще, в контексте записи вещественных чисел слова «точка» и «запятая» являются синонимами, например, можно сказать, что в числе 12.34 две цифры после запятой, хотя на самом деле я там написал точку. Или, например, фразы «с плавающей точкой» и «с плавающей запятой» обозначают одно и то же.

Но есть также и другой формат записи — так называемая запись чисел «с плавающей точкой». (По идее это должны проходить в школе классе эдак в 8, поэтому я описываю тут это в первую очередь для младшеклассников, а также для тех, кто успел забыть; ну и чтобы четко обозначить термины «мантисса» и «экспонента».)

При записи чисел с плавающей точкой запись имеет следующий вид: 1.234e1. Она состоит из двух частей, разделенных английской буквой e (может использоваться как маленькая, так и заглавная буква, хотя сейчас вроде чаще используют маленькую). Такая запись обозначает: «возьми число 1.234 и сдвинь в нем точку на 1 позицию направо» — соответственно, получается то же 12.34. Аналогично, возможна запись 0.1234e2 — взять число 0.1234 и сдвинуть точку на две позиции направо, это будет то же 12.34. Число после e может быть быть нулем, это значит, что точку сдвигать не надо: 12.34e0 — это то же самое, что 12.34. Число может быть отрицательным, что значит, что точку надо сдвигать влево, а не вправо: 123.4e-1 или 1234e-2 — это все тоже 12.34. (Обратите внимание, что в записи 1234e-2 вообще отсутствует точка — она тогда, конечно, неявно подразумевается на конце записи числа 1234, точно так же, как 1234 и 1234.0 — это одно и то же.)

То есть еще раз: 0.1234e2, 1.234e1, 12.34e0, 12.34, 123.4e-1, 1234e-2, и даже 123400e-4 и 0.001234e4 — это все записи одного и того же числа 12.34. Записи разные, число одно и то же.

Видно, что одно и то же число можно записать разными способами. Чаще пишут так, чтобы либо перед точкой была ровно одна ненулевая цифра (1.234e1), или чтобы перед точкой был ноль, зато сразу после точки шла ненулевая цифра (0.1234e2), но в целом любая из приведенных в предыдущем абзаце записей является правильной, и есть много правильных записей, которые не приведены выше.

Еще примеры: 1.3703599907444e2 и 13703599907444e-11 — это 137.03599907444.

Отрицательные числа записываются, естественно, с минусом перед самим числом: -1.234e1, или -1234e-2 — это то же самое, что и -12.34.

Иногда, особенно в печатной литературе (а до появления компьютеров — особенно часто) вместо записи через e используют эквивалентную запись через умножение на 10 в нужной степени, например, вместо 0.1234e2 пишут \(0.1234\cdot 10^2\) , вместо 123.4e-1 пишут \(1.234\cdot 10^<-1>\) и т.п. Несложно видеть, что это полностью эквивалентные записи, и что умножение на десять в нужной степени полностью эквивалентно сдвигу точки. На самом деле, насколько я понимаю, запись через e появилась как раз когда появились компьютеры, потому что запись через степень десятки довольно сложно, а иногда и невозможно, набирать на клавиатуре. Но сейчас, благодаря повсеместному распространению компьютеров, запись через e уже нередко встречается и в печатной литературе.

Запись чисел с плавающей точкой особенно удобна, когда вам надо хранить очень большие или очень маленькие числа. Например, расстояние от Земли до Солнца примерно 147 миллионов километров, т.е. 147000000000 метров. Так записывать очень неудобно, потому что надо тщательно считать нолики. Намного удобнее написать 147e9 — сразу понятно, что будет девять ноликов, и сразу понятно, что это 147 миллиардов. Или, например, атом водорода весит примерно 1.66e-24 грамм, т.е. 0.00000000000000000000000166 грамм (если я не ошибся в количестве ноликов 🙂 ). Ясно, что первая запись намного удобнее.

Эти две части, составляющие запись числа с плавающей точкой, называются «мантисса» — это часть до e , — и «экспонента» — это число после e . Например, в записи 1.234e1 мантисса равна 1.234, а экспонента равна 1.

2.6.2. Как компьютер хранит вещественные числа¶

Вещественные числа, с которыми может иметь дело компьютер, могут быть как очень большими, так и очень маленькими. С другой стороны, вещественные числа в принципе невозможно хранить абсолютно точно, т.к. в них могут быть очень много знаков (даже бесконечно много) после точки.

Поэтому компьютер хранит числа в записи с плавающей точкой, при этом он хранит мантиссу и экспоненту по отдельности (но рядом в памяти, конечно, и в конечном счете, конечно, для вас как для программиста это будет одна переменная, хранящая вещественное число, а не две отдельных переменных, хранящих мантиссу и экспоненту). Более того, поскольку вообще говоря в вещественных числах в мантиссе может быть бесконечно много цифр, компьютер хранит лишь несколько первых цифр мантиссы.

Вообще, на самом деле компьютер хранит числа в двоичной системе счисления (т.е. на самом деле компьютер хранит не десятичную экспоненту, как это было описано выше, а двоичную), но это вам будет пока не особенно важно, потому что весь ввод-вывод вещественных чисел использует все-таки десятичную экспоненту.

2.6.3. Типы данных¶

Все современные компьютеры умеют работать со следующими тремя типами данных:

• single — хранит 7-8 цифр мантиссы, экспоненту до примерно ±40, занимает в памяти 4 байта, работает сравнительно быстро;
• double — хранит 15-16 цифр мантиссы, экспонента до примерно ±300, занимает 8 байт, работает несколько медленнее;
• extended — хранит 19-20 цифр мантиссы, экспонента до примерно ±5000, занимает в памяти 10 байт, работает намного медленнее;

Уточню, что значит «столько-то цифр мантиссы» и «такая-то экспонента». Как я писал выше, в мантиссе хранится только несколько первых цифр. Собственно, в single хранится только 7-8 цифр, в double 15-16, в expended 19-20. То есть например, если вы попытаетесь в single записать число 1.234567890123456789e20, то на самом деле запишется примерно 1.234567e20, остальные цифры будут отброшены. (На самом деле все немного сложнее из-за того, что числа хранятся в двоичной системе счисления, собственно поэтому я и пишу 7-8 цифр, потому что на самом деле как повезет в плане двоичной системы счисления.)

Ограничение же на экспоненту обозначает, что числа со слишком большой экспонентой вы просто не сможете записать в нужный тип (например, 1.23e100 не влезет в single), будет или ошибка, или получится специальное значение «бесконечность»; а числа со слишком большой отрицательной экспонентой просто будут считаться равными нулю (если вы попробуете записать 1.23e-100 в single, то получится 0).

Эти типы поддерживаются процессором (т.е. процессор умеет выполнять команду «сложить два числа типа single» или «вычесть два числа типа extended» и т.п.). Поэтому эти типы присутствуют (возможно, с другими названиями) почти во всех существующих языках программирования.

К сожалению, конкретно в питоне нет простой возможности выбрать один из этих трех типов, можно работать только с double, причем в питоне вместо слова double используется название float (что вообще странно, потому что в других языках float — это single, а вовсе не double). Таким образом,

Стандартные вещественные числа в питоне называются float, хранят 15-16 цифр в мантиссе и экспоненту до примерно ±300.

2.6.4. Про «значащие цифры»¶

Как мы видели, одно и то же число можно записать с плавающей точкой по-разному. Чисто 12.34 можно записать как 0.0000000001234e11, и как 1234000000000e-11, и т.п. Конечно, компьютер будет хранить число каким-то конкретным образом. Более того, если, например, попробовать записать 0.0000000001234e11 например в single, то вы можете сказать, что будут записаны только нули (потому что мантисса хранит только 7-8 цифр).

На самом деле компьютер хранит числа чуть сложнее. В первом приближении можно считать, что компьютер хранит числа так, чтобы до точки была ровно одна ненулевая цифра (про это я писал выше), т.е. число 12.34 компьютер будет хранить как 1.234e-1 и никак иначе, а например расстояние от Земли до Солнца в метрах — как 1.47e11 и не иначе. (А на самом деле еще сложнее из-за двоичной системы счисления).

Поэтому компьютер никогда не будет хранить в мантиссе ведущих нулей. В этом смысле говорят о «значащих цифрах» — это цифры в записи числа, начиная с первой ненулевой цифры. Например, в числе 12.3405 значащие цифры — это 1, 2, 3, 4, 0, 5, а в числе 0.00000000000000000000000000166 значащие цифры — это 1, 6 и 6 (и компьютер будет хранить это число как 1.66e-27).

Поэтому говорят, что тип single хранит 7-8 значащих цифр, double — 15-16 значащих цифр, extended — 19-20.

2.6.5. Про дырки между числами¶

(Понимание про «дырки» для начальных задач не особо нужно, но в дальнейшем бывает полезно.)

Из-за того, что компьютер хранит строго определенное количество значащих цифр, получается, что между соседними числами конкретного типа есть «дыры». Например, пусть мы возьмем тип single. В него невозможно записать число 1.2345678901234 — можно записать только 1.234567 или 1.234568. Получается, что между числами 1.234567 или 1.234568 есть целая «дыра» длиной 0.000001, в которой нет ни одного числа, которое может храниться в single.

Когда сами числа не очень большие, то и «дыры» не очень длинные. Но когда числа становятся большими, то и «дыры» тоже становятся больше. Например, число 123456789 тоже невозможно записать в single, можно записать только 123456700 или 123456800 — «дыра» получается уже длины 100!

(На самом деле конкретные числа, которые возможно записать — они немного другие, опять же из-за двоичной системы счисления, и соответственно размеры «дырок» тоже другие, они будут степенями двойки, а не десятки, но качественно все описанное выше верно.)

2.6.6. Базовые операции¶

С вещественными числами доступны все привычные уже вам операции: +-*/, abs, sqrt, ввод-вывод через float(input()), map(float, …) и print. Также работает деление с остатком (// и %).

При этом в ваших программах, а также при вводе вы можете задавать числа как в записи с фиксированной точкой, так и с плавающей, т.е. вы можете писать, например, a = 1.23 + 2.34e-1; , и при считывании чисел можете вводить значения тоже как в формате 1.23 , так и в формате 2.34e-1 .

2.6.7. Про вывод подробнее¶

Часто в наших задачах вы можете встретить фразу «выведите ответ с точностью до 5 знаков после запятой», или «с пятью верными знаками» и т.п. Такие фразы почти всегда обозначают, что ваш ответ должен содержать 5 верных цифр после запятой, но они не запрещают вам выводить больше цифр. Вы можете вывести хоть 20 цифр — если первые пять из них верные, то ответ будет зачтен. И наоборот, вы можете вывести меньше цифр — если невыведенные цифры — нули, то ответ тоже будет зачтен. Вообще, строго говоря, такая фраза в условии просто обозначает, что ваш ответ должен отличаться от верного не более чем на 1e-5.

Пример: если правильный ответ на задачу — 0.123456789, то вы можете вывести 0.12345, или 0.123459876, или даже 1.2345e-1 (т.к. это то же самое, что и 0.12345). А если правильный ответ — 0.10000023, то вы можете вывести 0.10000, 0.10000987 или даже просто 0.1 или 1e-001 (т.к. это то же самое, что и 0.10000).

В частности, это обозначает, что вы можете пользоваться стандартной функцией вывода (print) без каких-либо особых ухищрений; не надо округлять число, не надо форматировать вывод и т.д.

Вот если в задаче строго сказано «вывести ровно с 5 знаками после запятой», то это другое дело. Но на приличных олимпиадах такое бывает очень редко.

2.6.8. Полезные функции¶

В питоне есть несколько функций, которые вам будут полезны при работе с вещественными числами. Для ряда из этих функций надо в самом начале программы написать from math import * (как вы уже писали для квадратного корня). Кроме того, имейте в виду, что с этими функциями также могут возникать проблемы погрешностей (см. ниже).

• floor («пол») — округляет число вниз, т.е. определяет ближайшее целое число, которое меньше или равно данного вещественного. Например, floor(2.4) == 2 , floor(2) == 2 , floor(-2.4) == -3 , и floor(2.8) == 2 .
• ceil («потолок») — округляет число вверх, т.е. определяет ближайшее целое число, которое больше или равно данного вещественного. Например, ceil(2.4) == 3 , ceil(2) == 2 , ceil(-2.4) == -2 , и ceil(2.8) == 3 .
• trunc — округляет число в сторону нуля. Например, trunc(2.4) == 2 , trunc(2) == 2 , trunc(-2.4)== -2 , и trunc(2.8) == 2 .
• round — округляет число к ближайшему целому числу («по школьным правилам», за исключением ситуации, когда дробная часть числа строго равна 0.5 — тогда в зависимости от числа может быть округление то в одну, то в другую сторону). Например, round(2.4) == 2 , round(2) == 2 , round(-2.4) == -2 , и round(2.8) == 3 .
• Еще повторю, что работают операции деления с остатком ( // и % ), в частности, x % 1 дает дробную часть числа x .

Пример программы, использующей эти функции:

2.6.9. Погрешности¶

2.6.9.1. Два правила работы с вещественными числами¶

Сначала напишу два главных правила работы с вещественными числами:

Правило первое: не работайте с вещественными числами. А именно, если возможно какую-то задачу решить без применения вещественных чисел, и это не очень сложно, то лучше ее решать без вещественных чисел.

Правило второе: если уж работаете, то используйте eps . При любых [1] сравнениях вещественных чисел надо использовать eps .

[1]	(1, 2) за исключением случаев, когда вам не важно, что произойдет в случае точного равенства, см. ниже

Ниже я разъясняю оба этих правила.

2.6.9.2. Необходимость использования eps ¶

Как уже говорилось выше, компьютер не может хранить все цифры числа, он хранит только несколько первых значащих цифр. Поэтому, если, например, разделить 1 на 3, то получится не 0.33333… (бесконечно много цифр), а, например, 0.33333333 (только несколько первых цифр). Если потом умножить результат обратно на 3, то получится не ровно 1, а 0.99999999. (Аналогичный эффект есть на простых калькуляторах; на продвинутых калькуляторах он тоже есть, но проявляется сложнее.)

(Вы можете попробовать потестировать, правда ли, что (1/3)*3 равно 1, и обнаружить, что проверка if (1 / 3) * 3 == 1 выполняется. Да, тут повезло — опять-таки из-за двоичной системы получилось округление в правильную сторону. Но с другими числами это может не пройти, например, проверка if (1 / 49) * 49 == 1 не срабатывает.)

На самом деле все еще хуже: компьютер работает в двоичной системе счисления, поэтому даже числа, в которых в десятичной системе счисления имеют конечное число цифр, в компьютере могут представляться неточно. Поэтому, например, сравнение if 0.3 + 0.6 == 0.9 тоже не сработает: если сложить 0.3 и 0.6, то получится не ровно 0.9, а слегка отличающее число (0.899999 или 0.900001 и т.п.)

Действительно, напишите и запустите следующую программу:

и вы увидите, что она выводит Fail.

(Более того, print(0.3+0.6) выводит у меня 0.8999999999999999.)

Итак, погрешности, возникающие при любых вычислениях, — это основная проблема работы с вещественными числами. Поэтому если вам надо сравнить два вещественных числа, то надо учитывать, что, даже если на самом деле они должны быть равны, в программе они могут оказаться не равны.

Стандартный подход для борьбы с этим — выбрать маленькое число eps (от названия греческой буквы ε — «эпсилон», «epsilon»), и два числа считать равными, если они отличаются не более чем на eps .

Про то, как выбирать это eps , обсудим ниже, пока будем считать, что мы взяли eps=1e-6 . Тогда в начале программы пишем

— и далее в коде когда нам надо сравнить два числа, мы вместо if x=y пишем if abs(x — y) eps , т.е. проверяем, правда ли, что \(|x-y| .

То есть мы предполагаем, что если два числа на самом деле должны быть равны, но отличаются из-за погрешности, то они отличаться будут менее чем на eps ; а если они на самом деле должны различаться, то различаться они будут более чем на eps . Таким образом, eps разделяет ситуации «два числа равны» и «два числа не равны». (Естественно, это будет работать не при любом eps , т.е. eps надо аккуратно выбирать — про это см. ниже.)

Аналогично, если нам надо проверить if x >= y , то надо писать if x >= y — eps или if x > y — eps . (Обратите внимание, что тут не важно, писать строгое или нестрогое равенство — вероятность того, что окажется точно x == y — eps очень мала из-за тех же погрешностей: скорее всего окажется или больше, или меньше. Более того, если оказалось, что точно x == y — eps , это обозначает, что мы неправильно выбрали eps , т.к мы не смогли отделить ситуацию «числа x и y равны» и ситуацию «числа не равны». См. еще ниже в разделе про выбор eps .)

Если нам надо написать условие if x > y , то его тоже надо переписать, ведь нам важно (подробнее см. ниже), чтобы при x == y условие не выполнилось! Поэтому переписать его надо так: if x > y + eps . Аналогичные соображения действуют для любых других сравнений вещественных чисел.

Итак, именно поэтому получаем

Правило второе: если уж работаете, то используйте eps . При любых [1] сравнениях вещественных чисел надо использовать eps .

(Первое правило будет дальше 🙂 )

2.6.9.3. Выбор eps ¶

Выбор eps — это весьма нетривиальная задача, и далеко не всегда она вообще имеет правильное решение. Нам надо выбрать такое eps , чтобы, если два числа должны быть равны (но отличаются из-за погрешностей), то их разность точно была меньше eps , а если они не равны, то точно была больше eps . Ясно, что в общем случае эта задача не имеет решения: может быть так, что в одной программе будут два числа, которые должны быть равны, но отличаются, например, на 0.1 из-за погрешности, и два числа, которые действительно различны, но отличаются только на 0.01.

Но обычно считают, что в «разумных» задачах все-таки такое eps существует, т.е. числа, которые должны быть равны, отличаются не очень сильно, а те, которые должны отличаться, отличаются намного сильнее. И eps выбирают где-нибудь посередине. (В частности, поэтому, как говорилось выше, не бывает так, что x == y — eps точно.) (В более сложных задачах может понадобиться применять более сложные техники, но мы их сейчас не будем обсуждать.)

В некоторых, самых простых, задачах такое eps можно вычислить строго. Например, пусть задача: даны три числа \(a\) , \(b\) и \(c\) , каждое не больше 1000, и каждое имеет не более 3 цифр после десятичной запятой. Надо проверить, правда ли, что \(a+b=c\) . Из изложенного выше понятно, что тупое решение if a + b == c не сработает: может оказаться, что должно быть \(a + b = c\) , но из-за погрешностей получится, что \(a+b \neq c\) . Поэтому надо проверять if abs(a + b — c) eps , но какое брать eps ?

Подумаем: пусть действительно \(a+b=c\) . Какой может быть разница \(a+b-c\) с учетом погрешностей? Мы знаем, что \(a\) , \(b\) и \(c\) не превосходят 1000. Мы используем тип данных float (который на самом деле double ), в котором хранятся 15-16 верных цифр, значит, погрешности будут примерно в 15-16-й значащей цифре. Для максимальных возможных значений чисел (т.е. для 1000) погрешности будут порядка 1e-12 или меньше, т.е. можно рассчитывать, что если \(a+b=c\) , то в программе \(|a+b-c|\) будет порядка 1e-12 или меньше.

С другой стороны, пусть \(a+b \neq c\) . Какой тогда может быть разница \(|a+b-c|\) ? По условию, все числа имеют не более трех цифр после запятой, поэтом понятно, что эта разница будет равна 0.001 или больше.

Итого мы видим, что если числа должны быть равны, то они отличаются не более чем на 1e-12 , а если не равны, то как минимум на 1e-3 . Поэтому можно, например, взять eps=1e-5 . С одной стороны, если на самом деле \(a+b=c\) , то в программе \(|a+b-c|\) точно получится намного меньше eps , а с другой стороны, если на самом деле \(a+b\neq c\) , то \(|a+b-c|\) будет точно намного больше eps . Итак, в этом примере мы смогли точно вычислить подходящее eps .

(И вообще, конечно, вариантов много — подошло бы любое число, которое существенно меньше 1e-3 и существенно больше 1e-12. Вот это и есть «хорошая» ситуация, когда варианты «равны» и «не равны» разделены очень сильно. А если бы они не были бы так разделены, то весь фокус с eps не прошел бы. Это то, про что я писал немного выше.).

Но бывают задачи, где так просто вычислить подходящее eps не получается. На самом деле таких задач большинство — как только вычисления у вас становятся сложнее чем сложить два числа, за погрешностями уже становится сложно уследить. Можно, конечно, применять какие-нибудь сложные техники, но обычно принято просто брать какое-нибудь eps порядка 1e-6 .. 1e-10 .

Но в итоге вы не можете быть уверены, что вы выбрали правильное eps . Если ваша программа не работает — это может быть потому, что у вас ошибка в программе, а может быть просто потому, что вы выбрали неверный eps . Бывает так, что достаточно поменять eps — и программа пройдет все тесты. Конечно, это не очень хорошо, но ничего не поделаешь.

В частности, поэтому на олимпиадах очень не любят давать задачи, которые реально требуют вычислений с вещественными числами — никто, даже само жюри, не может быть уверено в том, что у них eps выбрано верно. Но иногда такие задачи все-таки дают, т.к. никуда не денешься.

И поэтому получаем

Первое правило работы с вещественными числами: не работайте с вещественными числами. А именно, если возможно какую-то задачу решить без применения вещественных чисел, и это не очень сложно, то лучше ее решать без вещественных чисел, чтобы не думать про все эти погрешности и eps .

Пример: пусть у вас в программе есть четыре целых (int) положительных числа \(a\) , \(b\) , \(c\) и \(d\) , и вам надо сравнить две дроби: \(a/b\) и \(c/d\) . Вы могли бы написать if a / b > c / d , но это плохо: в результате деления получаются вещественные числа, и вы сравниваете два вещественных числа со всеми вытекающими последствиями. (Конкретно в этом случае, возможно, ничего плохого не случится, но в чуть более сложных случаях уже может случиться, да и в этом случае возможно и случится, я не проверял.) А именно, может оказаться, например, что \(a / b = c / d\) на самом деле, но из-за погрешностей в программе получится \(a/b>c/d\) и if выполнится. Вы можете написать eps , думать, каким его выбрать… но можно проще. Можно просто понять, что при положительных (по условию) числах это сравнение эквивалентно условию if a * d > c * b . Здесь все вычисления идут только в целых числах, поэтому это условие работает всегда, и не требует никаких eps (да еще и работает быстрее, чем предыдущий вариант). Его написать не сложнее, чем вариант с делением, поэтому всегда следует так и писать. Всегда, когда в решении вы переходите от целых к вещественным числам, задумайтесь на секунду: а нельзя ли обойтись без вещественных чисел? Если да, то постарайтесь так и поступить — и никаких проблем с точностью у вас не возникнет.

В частности, в будущем вы заметите, что во многих задачах, которые, казалось бы, подразумевают вещественные входные данные (например, задачи на геометрию), входные данные тем не менее обычно целочисленны. Это сделано именно для того, чтобы можно было написать решение полностью в целых числах, и не иметь проблем с погрешностью. (Не всегда такое решение возможно, и уж тем более не всегда оно простое, но тем не менее.) Поэтому если вы можете написать такое решение, лучше написать именно его.

2.6.10. Дополнительный материал. «Грубые» задачи: когда eps не нужно¶

Рассмотрим следующие код ( x , y , max – вещественные числа):

Здесь мы сравниваем два вещественных числа, чтобы найти максимум из них. Казалось бы, в соответствии со сказанным выше, в сравнении нужен eps … но нет! Ведь если два числа на самом деле равны, то нам все равно, в какую из веток if мы попадем — обе ветки будут верными! Поэтому eps тут не нужен.

Так иногда бывает — когда вам все равно, в какую ветку if’а вы попадете, если два сравниваемых числа на самом деле равны между собой. В таком случае eps использовать не надо. Но каждый раз тщательно думайте: а правда ли все равно? Всегда лучше перестраховаться и написать eps (выше с eps тоже все работало бы), за исключением совсем уж простых случаев типа приведенного выше вычисления максимума.

Еще пример: считаем сумму положительных элементов массива

Здесь, опять-таки, если должно быть \(x_i=0\) , то не важно, добавим мы его в сумму или нет: сумма от добавления нуля не изменится. Поэтому eps писать не надо (но ничего страшного не будет, если и написать).

Еще пример, где уже eps необходим: определим, какое из двух чисел больше:

Вообще, тут полезно следующее понятие. Назовем задачу (или фрагмент кода) грубым, если ответ на задачу (или результат работы этого фрагмента) меняется не очень сильно (не скачком) при небольшом изменении входных данных, и негрубым в противоположном случае. (Понятие грубости пришло из физики.)

Тогда в задаче (фрагменте кода) eps нужен, если задача является негрубой: тогда существуют такие входные данные, которые вам важно отличить от очень близких им. Например, если надо определить, какое из двух чисел больше, то при входных данных «0.3 0.3» надо ответить «они равны», но при очень небольшом изменении входных данных, например, на «0.300001 0.3» ответ резко меняется: надо отвечать «первое больше».

Если же задача (или фрагмент кода) является грубым, то, скорее всего, в нем можно обойтись без eps : если вы чуть-чуть ошибетесь при вычислениях, ответ тоже изменится не очень сильно. Например, если вы вычисляете максимум из двух чисел, то на входных данных «0.3 0.3» ответ 0.3, а на входных данных «0.300001 0.3» ответ 0.300001, т.е. изменился не очень сильно.

Но, конечно, все приведенное выше рассуждение про грубые задачи — очень примерно, и в каждой задаче надо отдельно думать.

2.6.11. Примеры решения задач¶

Приведу несколько примеров задач, аналогичных тем, которые встречаются на олимпиадах и в моем курсе.

Маша наблюдает из дома за грозой. Она увидела молнию, а через \(T\) секунд услышала гром от молнии. Она знает, что в той стороне, где была молния, есть одинокое дерево, и боится, не попала ли молния в это дерево. Расстояние от Машиного дома до дерева равно \(L\) метров, скорость звука равна \(V\) метров в секунду, скорость света считаем бесконечной. Определите, могла ли молния попасть в дерево.

Входные данные: На одной строке вводятся три вещественных числа — \(T\) , \(L\) и \(V\) .

Входные данные: Выведите yes , если молния могла попасть в дерево, и no в противном случае.

Пример:

Несложно понять, что расстояние от Машиного дома до молнии равно \(V\cdot T\) . Осталось проверить, равно ли это \(L\) . Можно было бы написать if v * t == l , но, поскольку все числа вещественные, так просто не заработает — из-за погрешностей результат умножания может оказаться не равен l , даже если на самом деле он должен быть равен. (Не говоря уж о том, что в реальной жизни значения \(V\) , \(L\) и \(T\) известны не совсем точно, и поэтому \(V\cdot T\) может оказаться не равно \(L\) банально из-за погрешностей измерения.) Поэтому надо проверять, что v*t примерно равно l , т.е. что разница abs(l — v * t) не слишком велика. Выберем какое-нибудь eps и будем сравнивать с ним.

Итоговый код получается такой:

Выбор eps тут в существенной мере произвольный, подробнее про выбор eps описано выше в основной части теории.

Вася проехал \(L\) километров за \(T\) часов. На той дороге, по которой он ехал, ограничение скорости \(V\) километров в час: можно ехать с любой скоростью, не превышающей \(V\) . Определите, нарушил ли Вася правила.

Входные данные: На одной строке вводятся три вещественных числа — \(T\) , \(L\) и \(V\) .

Входные данные: Выведите yes , если Вася нарушил правила, и no в противном случае.

Пример:

Скорость Васи равна \(L/T\) . Если она строго больше чем \(V\) , то Вася нарушил правила, иначе нет. Но надо помнить, что если \(L/T\) на самом деле точно равно \(V\) (как в примере), то из-за погрешностей может получиться \(L/T\) чуть больше \(V\) . Поэтому написать if l / t > v нельзя, это может выдать yes , если Вася ехал со скоростью ровно v . Надо добавить небольшой запас eps :

Обратите внимание, что по смыслу нам было нужно строгое сравнение \(L/T>V\) , и для учета погрешностей пришлось его переписать как l / t > v + eps . Если бы нам нужно было бы нестрогое сравнение \(L/T\geqslant V\) , то для учета погрешностей пришлось бы добавить запас с другой стороны, и написать l / t > v — eps . При этом в обоих случаях можно было бы писать и >= (например, l / t >= v — eps ), как раз это не имеет никакого значения. Значение имеет знак перед eps , т.е. делаем мы запас в одну или в другую сторону.

Источник