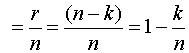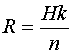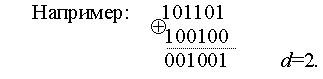Что значит вес кода

Что такое вес в каратах (ct) и общий вес в каратах (ctw)?

Если при покупке украшений с бриллиантами вы наткнулись на термины «вес в каратах» и «общий вес в каратах» и не знаете, что они означают, то вам лучше остановиться и прочитать эту статью полностью.

Причина, по которой я подчеркиваю это, заключается в том, что многие потребители вводятся в заблуждение рекламными заявлениями и двусмысленными описаниями ювелирных изделий. В руках неэтичного ювелира использование термина «общий вес в каратах» и маркетингового жаргона может привести к обману ничего не подозревающих покупателей.

Так что же это такое? Разве это не одно и то же?

Вес в каратах, обозначаемый как «CT» или «CW», представляет собой метрический вес одного бриллианта. Как вы узнали ранее, один карат равен двумстам миллиграммам, в этом нет ничего сложного.

Когда вы имеете дело с кольцом с одиночным бриллиантом или любым ювелирным изделием, содержащим один драгоценный камень, любое описание веса в каратах просто относится к весу этого отдельного бриллианта.

Что такое «общий вес в каратах» и почему используется этот термин?

Когда ювелирное изделие украшено несколькими бриллиантами, все становится немного сложнее. В описании ювелирных изделий применяется термин «общий вес в каратах».

В двух словах, общий вес в каратах относится к сумме веса всех бриллиантов в ювелирном изделии. Как правило, это сокращенно «CTW», «CWT», «TW» или «TDW».

Когда вы сталкиваетесь с ювелирными изделиями, использующими CTW в их описании, убедитесь, что вы дважды проверили детали используемых размеров бриллиантов. Важно, чтобы вы не пропустили этот шаг, и через мгновение я объясню, почему.

В торговле есть 2 основные причины использования термина CTW. Первая – для удобства, вторая – чтобы произвести впечатление. Теперь давайте сделаем небольшой тест.

Представьте себе, что вы читаете объявление, какое из следующих описаний вам больше понравится?

1) Получите больше за меньшее! В течение ограниченного времени купите это обручальное кольцо (TW) весом в 3 карата всего за $8,000!

2) Получите больше за меньшее! Купите это обручальное кольцо с 5 бриллиантами весом 0,6 карата каждый. Всего за $8,000!

Благодаря механизмам ценообразования, один крупный бриллиант будет стоить намного больше, чем эквивалентный вес меньших по размеру бриллиантов.

Как видно, пять бриллиантов весом 0,60 карата, купленных по отдельности, стоили бы всего $2 320 * 5 = $11 600. Напротив, одиночный камень весом 3 карата будет стоить почти в 5 раз дороже при цене $58 030.

Дело в том, что большинство потребителей предпочитают покупать бриллианты больших размеров (независимо от бюджета), и ювелиры это знают. По этой причине большинство предприятий рекламируют свои ювелирные изделия, используя общий вес в каратах, потому что это звучит очень впечатляюще, а низкие цены создают ложное впечатление о хорошей сделке.

Под сильным давлением, осуществляемым неэтичными продавцами, потребители, которые не знакомы с терминологией, часто обманываются и думают, что получают много, когда на самом деле это не так.

Давайте обратимся к математике, чтобы понять, что такое «общий вес в каратах».

Общий вес 100 мелких бриллиантов, каждый из которых весит 0,02 карата, равен весу одного 2-каратного бриллианта.

Вот простое уравнение, которое показывает это: 100 * 0,02 карата = 1 * 2,00 карата

Несмотря на то, что идея владения сотней бриллиантов может показаться некоторым людям привлекательной, единственный крупный камень более ценен в силу фактора редкости.

На самом деле 100 таких мелких бриллиантов F цвета VS чистоты будут стоить всего около $ 1200. Напротив, хорошо ограненный 2-каратный F бриллиант VS2 будет стоить до $25 000.

Важный вопрос при покупке ювелирных изделий с несколькими камнями

Если вы покупаете кольца с установленными несколькими бриллиантами, и есть центральный камень (обычно самый большой), не забудьте запросить полную информацию об этом бриллианте. Это потому, что центральный бриллиант обычно составляет основную часть стоимости кольца.

Это позволит вам оценить цену кольца и, следовательно, правильно рассчитать выгоду сделки.

При этом я знаю, что большинство ювелиров не хотят вводить потребителей в заблуждение со злым умыслом. Большинство из них просто хотят предложить потребителям выбор в пользу покупки чего-то грандиозного.

Не стоит бояться термина «общий вес в каратах», потому что он может быть полезной информацией, когда вы знаете, что он означает.

Источник

Код постоянного веса — Constant-weight code

В теории кодирования , A — код постоянного веса , также называется м -of- п — код , является обнаружение и исправление ошибок кода , где все кодовые слова одни и те же вес Хэмминга . Один горячий код и сбалансированный код широко используются два вида постоянного веса кода.

Теория тесно связана с теорией конструкций (таких как t- конструкции и системы Штейнера ). Большая часть работ в этой области дискретной математики связана с двоичными кодами постоянного веса.

Двоичные коды с постоянным весом имеют несколько применений, включая скачкообразную перестройку частоты в сетях GSM . В большинстве штрих-кодов используется двоичный код с постоянным весом, чтобы упростить автоматическую установку порога яркости, который различает черные и белые полосы. В большинстве линейных кодов используется либо код с постоянным весом, либо парный код диспаратности с почти постоянным весом . Помимо использования в качестве кодов исправления ошибок, большое пространство между кодовыми словами также можно использовать при проектировании асинхронных схем, таких как схемы, нечувствительные к задержке .

Коды с постоянным весом, как и коды Бергера , могут обнаруживать все однонаправленные ошибки.

СОДЕРЖАНИЕ

А ( п , д , ш )

Центральная проблема, связанная с кодами постоянного веса, заключается в следующем: каково максимальное количество кодовых слов в двоичном коде постоянного веса с длиной , расстоянием Хэмминга и весом ? Этот номер называется . п <\ displaystyle n> d <\ displaystyle d> ш <\ displaystyle w> А ( п , d , ш ) <\ Displaystyle А (п, д, ш)>

За исключением некоторых тривиальных наблюдений, обычно невозможно вычислить эти числа прямым способом. Верхние оценки даются несколькими важными теоремами, такими как первая и вторая границы Джонсона , а лучшие верхние оценки иногда можно найти другими способами. Нижние границы чаще всего находятся путем отображения конкретных кодов либо с использованием различных методов из дискретной математики, либо путем интенсивного компьютерного поиска. Большая таблица таких рекордных кодов была опубликована в 1990 году, а расширение на более длинные коды (но только для тех значений и, которые актуальны для приложения GSM) было опубликовано в 2006 году. d <\ displaystyle d> ш <\ displaystyle w>

Коды 1 из N

Особым случаем кодов с постоянным весом являются коды один из N , которые кодируют биты в кодовом слове битов. Код «один из двух» использует кодовые слова 01 и 10 для кодирования битов «0» и «1». Один из четырех кодов может использовать слова 0001, 0010, 0100, 1000 для кодирования двух битов 00, 01, 10 и 11. Примером является кодирование с двумя направляющими и звено цепи, используемое в схемах, нечувствительных к задержке. Для этих кодов и . бревно 2 ⁡ N <\ displaystyle \ log _ <2>N> N <\ displaystyle N> п знак равно N , d знак равно 2 , ш знак равно 1 <\ Displaystyle п = N,

w = 1> А ( п , d , ш ) знак равно п <\ Displaystyle А (п, d, ш) = п>

Некоторые из наиболее заметных применений однократных кодов включают в себя двухфазный код метки, использующий код 1 из 2; Позиционно-импульсная модуляция использует код 1 из n ; адресный декодер и т. д.

Сбалансированный код

В теории кодирования , A сбалансированный код является двоичным прямым исправлением ошибок кода , для которого каждое кодовое слово содержит равное число нулевых и единичных битов. Сбалансированные коды были введены Дональдом Кнутом ; они представляют собой подмножество так называемых неупорядоченных кодов, которые представляют собой коды, обладающие тем свойством, что позиции единиц в кодовом слове никогда не являются подмножеством позиций единиц в другом кодовом слове. Как и все неупорядоченные коды, сбалансированные коды подходят для обнаружения всех однонаправленных ошибок в закодированном сообщении. Сбалансированные коды обеспечивают особенно эффективное декодирование, которое может выполняться параллельно.

Некоторые из наиболее заметных применений кодов со сбалансированным весом включают в себя двухфазный код метки, использующий код 1 из 2; При кодировании 6b / 8b используется код 4 из 8; код Адамара является из кода (за исключением нулевого кодового слова), то три из шести- кода; и т.п. 2 k — 1 <\ displaystyle 2 ^ > 2 k <\ displaystyle 2 ^ >

Трехпроводное кодирование дорожек, используемое в MIPI C-PHY, можно рассматривать как обобщение кода с постоянным весом на троичный — каждый провод передает троичный сигнал , и в любой момент один из 3 проводов передает низкий уровень, один — передает средний, а один передает высокий сигнал.

m -of- n кодов

An M -of- п код является разъемные обнаружения ошибок кода с длиной кодового слова из п битов, где каждый кодовое слово содержит ровно т экземпляров «один». Одна битовая ошибка приведет к тому, что кодовое слово будет иметь либо m + 1, либо m — 1 «единиц». Пример кода m -of- n — это код 2 из 5, используемый Почтовой службой США .

Самая простая реализация — добавить строку из единиц к исходным данным до тех пор, пока она не будет содержать m единиц, а затем добавить нули для создания кода длины n .

Код 3 из 6

Исходные 3 бита данных	Добавленные биты
000	111
001	110
010	110
011	100
100	110
101	100
110	100
111	000

Некоторые из наиболее заметных применений кодов с постоянным весом, помимо уже упомянутых выше кодов с одним горячим и сбалансированным весом, включают: Code 39 использует код 3 из 9; В двоичном десятичном коде используется код 2 из 7, код 2 из 5 и т. д.

Источник

Электронные средства сбора, обработки и отображения информации

Оглавление

Помехоустойчивое кодирование

Понятие корректирующего кода

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.

Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).

В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.

Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.

Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды.

При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.

При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Общие принципы использования избыточности

Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть различных входных последовательностей и различных выходных последовательностей. Из общего числа выходных последовательностей только последовательностей соответствуют входным. Будем называть их разрешенными кодовыми комбинациями. Остальные ( — ) возможных выходных последовательностей для передачи не используются. Их будем называть запрещенными кодовыми комбинациями.

Искажение информации в процессе передачи сводится к тому, что некоторые из передаточных символов заменяются другими — неверными. Каждая из разрешенных комбинаций в результате действия помех может трансформироваться в любую другую. Всего может быть · возможных случаев. В это число входит:

— случаев безошибочной передачи;

— ·(-1) случаев перевода в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам;

— ·( — ) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.

Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:

К_обн .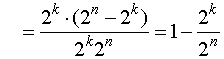

Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит , то есть вдвое больше общего числа кодируемых входных последовательностей. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество комбинаций, содержащих четное число единиц (или нулей). При кодировании к каждой последовательности из k информационных символов добавляется один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Искажение любого четного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть обнаруженных ошибок составляет:

К_обн .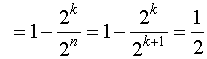

Пример кодирующего устройства с проверкой на четность показан на рис.

Основные параметры корректирующих кодов

Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.

Рассмотрим суть этих параметров.

Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов

Относительной избыточностью корректирующего кода называют величину

_отн

_отн.

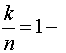
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.

Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна

поскольку в последовательности из п символов только k информационных.

Рис. 2.5 — Кодер с контролем на четность

Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.

Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.

Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.

Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.

Число обнаруживаемых ошибок определяется минимальным расстоянием между кодовыми комбинациями. Это расстояние называется хэмминговым.

В безызбыточном коде все комбинации являются разрешенными, =1. Достаточно только исказиться одному символу, и будет ошибка в сообщении.

Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.

Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как =1. Если =2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию.

Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:

000, 011, 101, 110 — разрешенные комбинации;

001, 010, 100, 111 — запрещенные комбинации.

Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности — минимальное хэммингово расстояние должно быть, по крайней мере, на единицу больше , то есть

+1.

В этом случае никакая ошибка кратности не в состоянии перевести одну разрешенную комбинацию в другую.

Ошибки можно не только обнаруживать, но и исправлять.

Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.

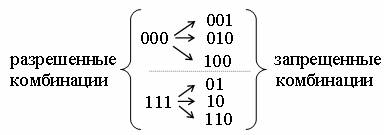
Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.

Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:

В общем случае исправляемые ошибки кратности связаны с кодовым расстоянием соотношением

=2+1. (2.1)

Для ориентировочного определения необходимой избыточности кода при заданном кодовом расстоянии d можно воспользоваться верхней граничной оценкой для r = n — k, называемой оценкой Хэмминга:

r = n — k ,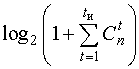

где — сочетание из п элементов по t (число возможных ошибок кратности t на длине п-разрядной комбинации).

Если, например, п=7, =1, то из (2.1)

=3, n — k (1+7)=3 .

Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.

Групповой код с проверкой на четность

Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:

Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы . Контрольные символы образуются путем суммирования по модулю 2 информационных символов, расположенных в столбце:

.

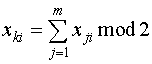
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.

Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).

Если проверка проводится по строкам и столбцам, то код называется матричным.

Проверочные символы располагаются следующим образом:

;

.

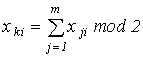
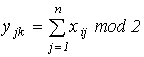
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.

Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.

Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.

Коды с постоянным весом

Весом называется число единиц, содержащихся в кодовых комбинациях.

Если число единиц во всех комбинациях кода будет постоянным, то такой код будет кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, поскольку здесь невозможно выделить информационные и проверочные символы. Наибольшее применение получили коды «3 из 7», «3 из 8», хотя возможны другие варианты. Первая цифра указывает на вес кода, вторая — на общее число символов в комбинации.

Разрешенными комбинациями кода «3 из 7» являются такие, которые содержат три единицы независимо от их места в комбинации, например 1110000 или 1010100 и т.д. Обнаружение ошибок сводится к определению их веса. Если вес отличается от заданного, то считается, что произошла ошибка. Код обнаруживает веса ошибок нечетной кратности и части ошибок четной кратности. Не обнаруживаются ошибки, при которых несколько единиц превращается в нули и столько же нулей — в единицы (ошибки смещения), так как при этом вес кода не изменяется.

В коде «3 из 7» возможных комбинаций сто двадцать восемь (=128), а разрешенных кода только тридцать пять. Относительная избыточность _отн = 0,28.

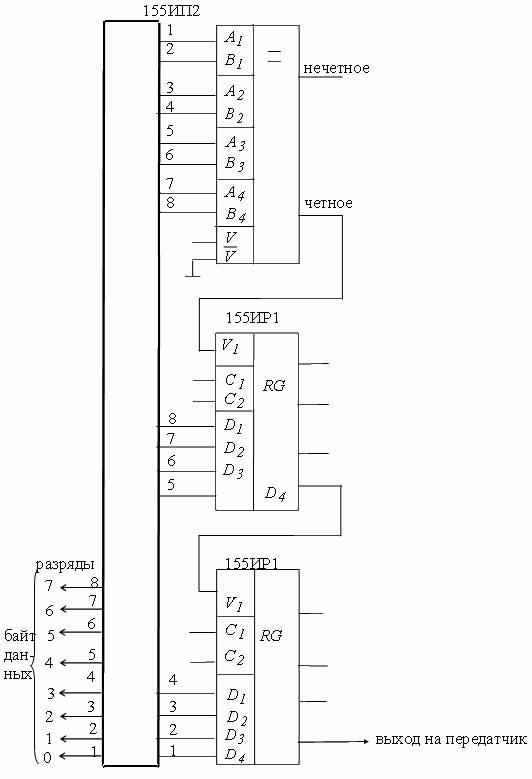
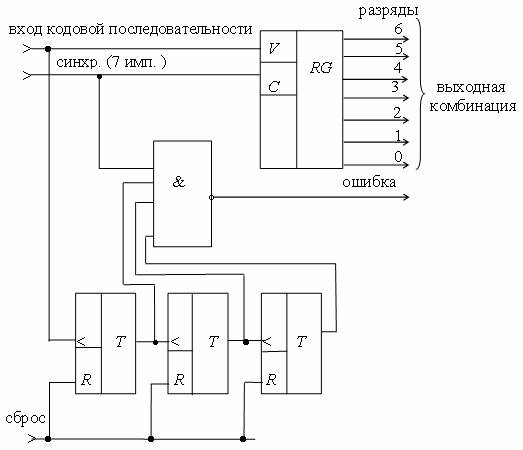
Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.

Рис. 2.6 — Схема определения веса комбинаций кода «3 из 7»

Циклические коды

Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.

— комбинация циклического кода;

— также комбинация циклического кода.

При рассмотрении циклических кодов двоичные числа представляют в виде многочлена, степень которого (п — 1), п — длина кодовой комбинации.

Например, комбинация 1001111 (п=7) будет представлена многочленом

При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.

Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.

Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:

• если старшая степень произведения не превышает (п — 1), то полученный полином будет представлять кодовую комбинацию циклического кода;
• если старшая степень произведения больше или равна п, то полином произведения делится на заранее выбранный полином степени п и результатом умножения считается полученный остаток от деления.

Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.

Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=+1. При таком формировании кодовых комбинаций позиции информационных и контрольных символов заранее определить нельзя.

Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.

Число разрядов регистра выбирается равным степени образующего полинома.

Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.

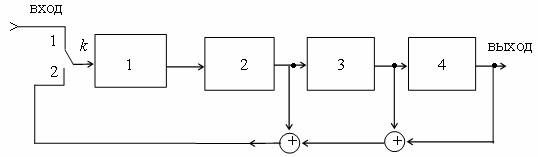
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.

Рис. 2.7 — Схема кодирующего регистра

В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.

Свойства циклического кода:

1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;

2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;

3) циклический код с образующим полиномом G(x) степени r = n — k обнаруживает все групповые ошибки длительностью в r символов.

Источник