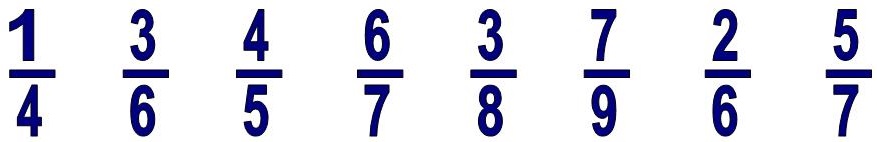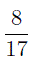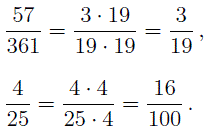Что значит величина дроби

Дроби и доли.

Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.

В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:

Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.

Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).

«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.

А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.

читается – две третьих, можно заменить по-другому — 2 : 3.

Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.

Что мы делаем? Вы берем нож и режем его пополам. Одну половину оставляем себе, а вторую отдадим другу. Сколько получал каждый? Он получал половину, то есть одну вторую.

Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.

Давайте посмотрим на число:

Что же это значит?

По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.

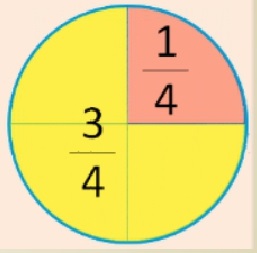
Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.

Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.

Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?

Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.

У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.

Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».

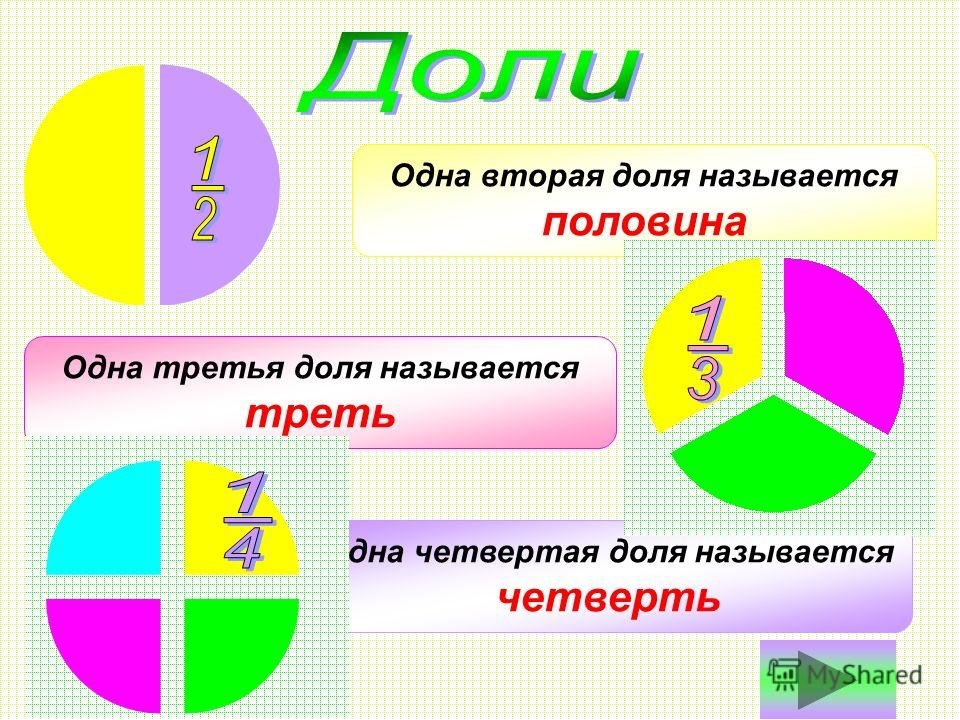
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.

Мы постоянно сталкиваемся с ними в жизни.

Чаще всего мы встречаемся в жизни именно с половиной:

пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.

Так же мы знакомы с одной третьей:

– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.

Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 81

Источник

Обыкновенные дроби

Вы будете перенаправлены на Автор24

Определение обыкновенной дроби

Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.

Яблоко разделили на $8$ долей. В этом случае каждая доля представляет одну восьмую долю целого яблока, т. е. $\frac<1><8>$. Две доли обозначаются $\frac<2><8>$, три доли — $\frac<3><8>$ и т.д., а $8$ долей — $\frac<8><8>$. Каждая из представленных записей называется обыкновенной дробью.

Приведем общее определение обыкновенной дроби.

Обыкновенной дробью называется запись вида $\frac$, где $m$ и $n$— любые натуральные числа.

Часто можно встретить следующую запись обыкновенной дроби: $m/n$.

Примеры обыкновенных дробей:

Числа $\frac<\sqrt<2>><3>$, $-\frac<13><37>$, $\frac<4><\frac<2><7>>$, $\frac<2,4><8,3>$ не являются обыкновенными дробями, т.к. не подходят под вышеприведенное определение.

Числитель и знаменатель

Обыкновенная дробь состоит из числителя и знаменателя.

Числителем обыкновенной дроби $\frac$ называется натуральное число $m$, которое показывает количество взятых равных долей из единого целого.

Знаменателем обыкновенной дроби $\frac$ называется натуральное число $n$, которое показывает, на сколько равных долей разделено единое целое.

Готовые работы на аналогичную тему

Числитель располагается над дробной чертой, а знаменатель —под дробной чертой. Например, числителем обыкновенной дроби $\frac<5><17>$ является число $5$, а знаменателем — число $17$. Знаменатель показывает, что предмет разделен на $17$ долей, а числитель — что взято $5$ таких долей.

Натуральное число как дробь со знаменателем 1

Знаменателем обыкновенной дроби может быть единица. В таком случае считают, что предмет неделим, т.е. представляет собой единое целое. Числитель такой дроби показывает, сколько целых предметов взято. Обыкновенная дробь вида $\frac<1>$ имеет смысл натурального числа $m$. Таким образом получаем обоснованное равенство $\frac<1>=m$.

Если переписать равенство в виде $m=\frac<1>$, то оно даст возможность любое натуральное число $m$ представить в виде обыкновенной дроби. Например, число $5$ можно представить в виде дроби $\frac<5><1>$, число $123 \ 456$ — это дробь $\frac<123\ 456><1>$.

Таким образом, любое натуральное число $m$ можно представить в виде обыкновенной дроби со знаменателем $1$, а любую обыкновенную дробь вида $\frac<1>$ можно заменить натуральным числом $m$.

Дробная черта как знак деления

Представление предмета в виде $n$ долей является делением на $n$ равных частей. После деления предмета на $n$ долей его можно разделить поровну между $n$ людьми — каждый получит по одной доле.

Пусть имеется $m$ одинаковых предметов, разделенных на $n$ долей. Эти $m$ предметов можно поровну разделить между $n$ людьми, если раздать каждому человеку по одной доле от каждого из $m$ предметов. При этом каждый человек получит $m$ долей $\frac<1>$, которые дают обыкновенную дробь $\frac$. Получаем, что обыкновенная дробь $\frac$ может применяться для обозначения деления $m$ предметов между $n$ людьми.

Связь между обыкновенными дробями и делением выражается в том, что дробную черту можно понимать как знак деления, т.е. $\frac=m:n$.

Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.

Например, результат деления $7$ яблок на $9$ человек можно записать как $\frac<7><9>$, т.е. каждый получит семь девятых долей яблока: $7:9=\frac<7><9>$.

Равные и неравные обыкновенные дроби, сравнение дробей

Результатом сравнения двух обыкновенных дробей может быть или их равенство, или их не равенство. При равенстве обыкновенных дробей их называют равными, в другом случае обыкновенные дроби называют неравными.

Выяснить, являются ли равными дроби $\frac<1><3>$ и $\frac<2><6>$.

Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:

Равенство выполняется, значит, дроби $\frac<1><3>$ и $\frac<2><6>$ являются равными: $\frac<1><3>=\frac<2><6>$.

Данный пример можно рассмотреть на примере яблок: одно из двух одинаковых яблок разделено на три равные доли, второе — на $6$ долей. При этом видно, что две шестых доли яблока составляют $\frac<1><3>$ долю.

Проверить, являются ли равными обыкновенные дроби $\frac<3><17>$ и $\frac<4><13>$.

Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:

\[3\cdot 13\ne 17\cdot 4;\] \[39\ne 58.\]

Равенство не выполняется, значит, дроби $\frac<3><17>$ и $\frac<4><13>$ не равны: $\frac<3><17>\ne \frac<4><13>$.

При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая — меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.

Дроби на координатном луче

Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче.

Чтобы на координатном луче отметить точку, которая соответствует дроби $\frac$, необходимо от начала координат в положительном направлении отложить $m$ отрезков, длина которых составляет $\frac<1>$ долю единичного отрезка. Такие отрезки получают при делении единичного отрезка на $n$ равных частей.

Чтобы отобразить на координатном луче дробное число, нужно единичный отрезок разделить на части.

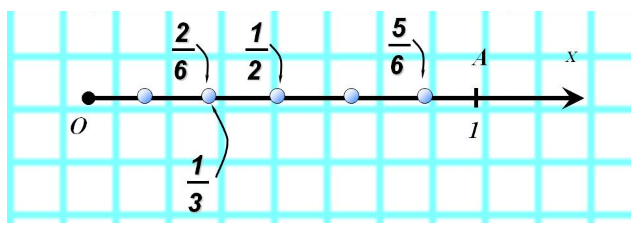
Равные дроби описываются одним и тем же дробным числом, т.е. равные дроби представляют собой координаты одной и той же точки на координатном луче. Например, координатами $\frac<1><3>$, $\frac<2><6>$, $\frac<3><9>$, $\frac<4><12>$ описывается одна и та же точка на координатном луче, так как все записанные дроби равны.

Если точка описывается координатой с большей дробью, то она будет находится правее на горизонтальном направленном вправо координатном луче от точки, координатой которой является меньшая дробь. Например, т.к. дробь $\frac<5><6>$ больше дроби $\frac<2><6>$, то и точка с координатой $\frac<5><6>$ находится правее точки с координатой $\frac<2><6>$.

Аналогично, точка с меньшей координатой будет лежать левее точки с большей координатой.

Источник

Дробь. Правильные и неправильные дроби. Смешанные числа

Содержание

Дробь. Числитель и знаменатель дроби

Правильные и неправильные дроби. Смешанные числа

Основное свойство дроби, сокращение дробей, несократимая дробь

Дробь. Числитель и знаменатель дроби

ОПРЕДЕЛЕНИЕ 1 . Дробью называют одну или несколько одинаковых долей (частей) предмета или некоторой величины.

Дробь записывают при помощи двух натуральных чисел, одно из которых стоит над горизонтальной чертой, а второе – под нею.

ОПРЕДЕЛЕНИЕ 2 . Число, стоящее над чертой, называют числителем дроби. Число, стоящее под чертой, называют знаменателем дроби.Числитель и знаменатель называют членами дроби.

Знаменатель дроби показывает, на сколько одинаковых долей мы делим предмет или величину, а числитель дроби показывает, сколько таких долей взято.

у которой числитель равен 8 , а знаменатель равен 17 , означает, что предмет или величину мы делим на 17 равных долей (частей) и берем 8 таких долей.

ПРИМЕР 1 . В классе 25 учеников, из которых 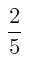посещают театральный кружок. Сколько учеников ходят в театральный кружок?

РЕШЕНИЕ . Для решения примера нужно 25 учеников разделить на 5 частей и взять 2 таких части.

ОТВЕТ . 10 учеников.

ПРИМЕР 2 . Турист в первый день похода прошел 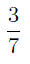намеченного маршрута, а во второй день – оставшиеся 24 километра. Сколько всего километров прошел турист?

РЕШЕНИЕ . Весь маршрут разделен на 7 равных частей, 3 из которых турист прошел в первый день (рис. 1).

1 день

1 день

1 день

2 день

2 день

2 день

2 день

Из рисунка 1 видно, что 24 километра составляют 4 из 7 частей маршрута. Таким образом, 1 часть маршрута равна

а весь маршрут равен

(км) .

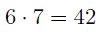
ОТВЕТ . 42 километра.

ЗАМЕЧАНИЕ. Если не указано, от какого предмета или какой величины берется дробь, то считают, что дробь взята от числа 1 .

Термин дробь имеет синонимы: простая дробь, обыкновенная дробь, рациональная дробь, дробное число.

Правильные и неправильные дроби. Смешанные числа

ОПРЕДЕЛЕНИЕ 3 . Если у дроби числитель меньше знаменателя, то ее называют правильной дробью. В противном случае – неправильной дробью.

Из этого определения, в частности, вытекает, что правильная дробь меньше единицы, а неправильная — больше единицы или равна единице.

– правильная дробь, и – неправильные дроби.

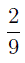
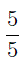
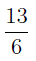
Неправильную дробь всегда можно представить в виде суммы целого числа и правильной дроби. Эту операцию называют выделением целой части из неправильной дроби и осуществляют при помощи деления с остатком числителя неправильной дроби на знаменатель.

Число 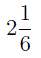является примером смешанного числа. Целое число 2 и правильную дробь называют целой и дробной частью смешанного числа соответственно.

Любое смешанное число всегда можно обратить в неправильную дробь, например,

Основное свойство дроби, сокращение дробей, несократимая дробь

Основным свойством дроби называют следующее

УТВЕРЖДЕНИЕ . Дробь превращается в равную дробь, если её числитель и знаменатель умножить или разделить на одно и то же число.

ОПРЕДЕЛЕНИЕ 4 . Операцию, при которой числитель и знаменатель дроби делят на одно и то же число, называют сокращением дроби.

ОПРЕДЕЛЕНИЕ 5 . Если числитель и знаменатель дроби не имеют общих делителей, то такую дробь называют несократимой.

При помощи сокращений любую дробь можно превратить в равную ей несократимую дробь.

Источник