Что значит утроенная разность чисел

Что такое утроенная разность чисел? Примеры?

Как записать утроенную разность чисел a и b?

Я думаю это как раз разность этих чисел, умноженная на 3. Здесь не оговаривается эта разность должна быть положительным числом или любым. Потому что от того из какого числа вычесть другое будет зависеть знак результата. Можно посчитать по модулю. Модуль 3*(a-b).

-8*3=-24. Модуль этого числа 24.

На мой взгляд это будет как-то так:(a-b)*3,где (a-b)- это разность чисел «a» и «b».Цифра «3»- это множитель. Тогда и получается утроенная разность чисел a и b. Здесь главное не перепутать с возведением в третью степень ((a-b)^3) и с разностью утроенных чисел «a» и «b» (3a- 3b).Как-то так, на мой взгляд получается.

Наверно так. Давно правда это было,но хочется вспомнить a—b=3x или 8—5=3×3, если объясняете ребенку,обязательно вспомните с ним,что такое разность ,утроенное,значит умноженное на три.

В пятом классе в учебнике по математике попадались такие задачи.

Нужно записать в буквенном выражении утроенную разность чисел a и b.

Утроенная, значит умноженная на три.

Для этого А и В нужно выделить скобками и умножить на 3.

Пишем (a-b)*3 или 3(a-b)

Нет одной «волшебной» формулы. Есть примеры, предназначенные специально для того, чтоб их долго решали, так как они направлены на развитие счета в уме. Но есть и примеры, предназначенные для решения по формулам.

В школе Вас могли учить «формулам сокращенного умножения», выносу за скобки и группировке.

Формул много, каждая для отдельного случая.

-вынос за скобки

ab+ac = a(b+c)

25 * 254 — 25 * 250 = 25 * (254 — 250) = 25 * 4 = 100

Вспомните основное правило раскрытия скобок — если перед скобкой стоит знак «минус», то стоящий за скобкой знак меняется на противоположный.

Если стоит «плюс», то знак за скобкой остается без изменения.

В Вашем примере перед скобкой стоит «плюс», следовательно, суммируем следующие числа -3 и -45 и получаем в ответе -48 (минус сорок восемь).

Если в четыре раза меньше, то это 41х и 82х, у каждого этого набора по 10 вариантов единиц, следовательно, таких чисел 20 штук:

410, 411, 412. 419,

820, 821, 822. 829.

Это двоичный код. Если у двоичного числа все нули заменить на единицы, а все единицы — на нули, то получится обратный код. При сложении с исходным числом, он дает все единицы в сумме. А если к обратномку коду прибавить один, то получится дополнительный код, который при сложении дает все нули. Это используется для подсчета контрольных сумм.

Казалось бы, в извлечении корня нет никакой сложности — используется метод последовательных приближений, например, метод половинного деления для решения уравнения x^2=a, придуманный для извлечения корня еще в Вавилоне. Однако 12-разрядное число — это 40 двоичных бит, то есть уравнение с заданной точностью решается за 40 итераций, на каждой из которых необходимо возводить в квадрат, то есть совершать весьма медленную операцию умножения. При отсутствии быстродействующего аппаратного умножителя (наличие которого трудно ожидать в калькуляторе) каждое умножение (в той же 12-разрядной сетке, которая 40 бит) выливается в

40 сложений и 40 сдвигов, к которым добавляются проверки условий и условные переходы. В результате только одних математических операций (сложений и сдвигов) за одно извлечение корня придется выполнить 3200 штук, плюс еще столько же вспомогательных.

Это сегодня процессор, выполняющий 50 миллионов операций в секунду и выполняющий 32-разрядное умножение (как и сложение) за один такт, стоит меньше доллара. Но раньше было не так, и чтобы калькулятор помещался на столе и стоил не как спортивный автомобиль или даже квартира в центре Нью-Йорка, разработчики были вынуждены сильно упрощать вычислительные блоки. Никаких параллельных АЛУ, все операции — последовательные, бит за битом. Операция сложения 12-разрядных чисел разворачивается в 48 операций двоичного сложения (48 — потому что использовалась двоично-десятичная кодировка, опять же, ради упрощения схемы), каждая — в лучшем случае за один такт. Тактовая частота — килогерцы, сложение за десятки миллисекунд, умножение — за полсекунды. Извлечение корня по такому алгоритму заняло бы десятки секунд.

Метод Ньютона, взятый «в лоб», ускоряет сходимость, да требует деления. А оно страшно долгое и выигрыша не получается.

Поэтому в калькуляторах применили алгоритмы, которые еще в доэлектронную эру использовали для извлечения корня на бумаге, а позже на арифмометре. Только с учетом того, что деление — операция долгая, как я говорил, а вот сдвиг — то же деление, только на 2,4 и т.д.

Источник

Как найти разность чисел в математике

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

• Арифметические действия с числами
• Разность в математике
• Как найти разницу величин
• Математические действия с разностью чисел
• Простые примеры
• Более сложные примеры
• Математика для блондинок

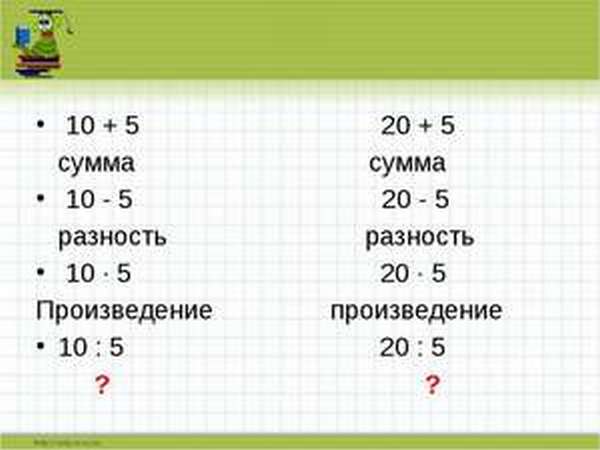
Арифметические действия с числами

Основными арифметическими действиями в математике являются:

Каждый результат этих действий также имеет своё название:

• сумма — результат, получившийся при сложении чисел,
• разность — результат, получившийся при вычитании чисел,
• произведение — результат умножения чисел,
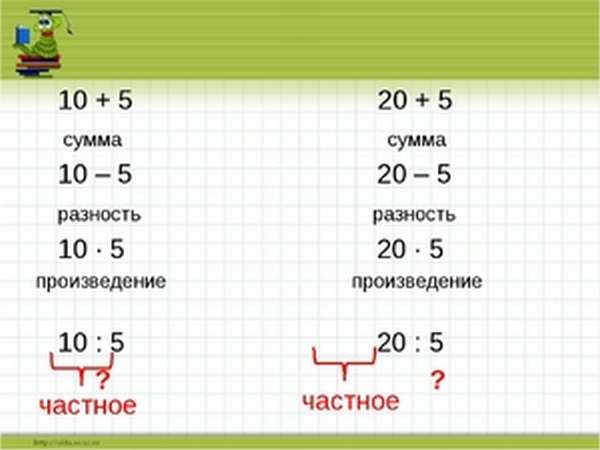
• частное — результат деления.

Это интересно: что такое модуль числа?

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

• сумма — прибавить,
• разность — отнять,
• произведение — умножить,
• частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

• Разность чисел означает, насколько одно из них больше другого.
• Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
• Это вычитание одного числа из другого.
• Это цифра, составляющая остаток при минусовании двух величин.
• Это величина, являющаяся результатом вычитания двух значений.
• Разность показывает количественное различие между двумя цифрами.
• Это результат одного из четырёх арифметических действий, которым является вычитание.
• Это то, что получится, если из уменьшаемого отнять вычитаемое.

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

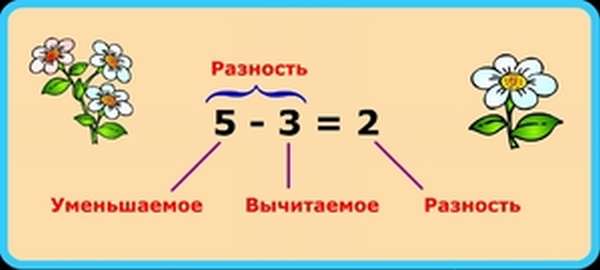
• Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

• Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

• Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
• Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Простые примеры

• Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

• Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

• Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

• Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),

Ответ: 40 — разница трёх значений.

• Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

• Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

• Удвоенное число — это величина, умноженная на два.
• Утроенное число — это величина, умноженная на три.
• Удвоенная разность — это разница величин, умноженная на два.
• Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

• Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина,

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

• Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

• сумму — сложением слагаемых,
• произведение — умножением множителей,
• частное — делением делимого на делитель.

Источник

Разность утроенного числа k и половины числа s

функции sin x и cos x периодические. Период 2pi

5.2 и 5.3
a) f`(x)=0 при х=-2 х=1 х=3
Касательная к графику функции в этих точка параллельна оси ох
Эти точки называют стационарными точками.

При переходе через эти точки производная меняет знак.
Если с + на — , то точка максимума
если с — на + точка минимума

Поэтому х=1 точка локального максимума
х=-2 х=3- точки локального минимума

Точки максимума и минимума также называют точками экстремума функции

Максимум равен 2 при х=1
минимум равен -3 при х=-2

Локальный максимум равен 2 при х=1
Локальный минимум равен
-1 при х=3
-3 при х=-2

б) f`(x)=0
при х=1 х=3
это стационарные точки, в них касательная параллельна оси ох
это и точки экстремума
в них производная меняет знак с — на +, поэтому
х=1 и х=3 — точки минимума

производная не существует в точках

х=-1 х=2
это критические точки
график функции в этих точках имеет изгиб ( излом)
Но при переходе через эти точки производная тоже меняет знак с+ на — и потому эти точки являются точками максимума

максимум равен 3 при х=-1
минимум равен 0 при х=1 и х=3

локальный экстремум
при х=-1 равен 3
при х=1 х=3 равен 0
при х=2 равен 1

Источник