БОРЬБА С ЦЕНТРОБЕЖНОЙ СИЛОЙ

Сегодня мы расскажем вам о физическом явлении, доставляющем всем моделистам и техникам много неприятностей. Имя ему — дисбаланс. Предложим и оружие, которым можно его одолеть.

КОМУ ОНА МЕШАЕТ?

Что такое центробежная сила, знают даже те, кто еще не изучал механику. Всем ведь приходилось вертеть на пальце игрушку, привязанную ниткой. Сила, с которой игрушка тянет вас за палец, и есть центробежная. Более строго говоря, центробежная сила — это сила воздействия на ось вращения со стороны вращающегося тела. Подобные силы сопровождают всякое вращение. Но кому же понадобилось бороться с ними и зачем? На этот вопрос в первую очередь может ответить тот, кто сам стирает белье в стиральной машине. Вспомним, как отжимают белье при машинной стирке. Если белье внутри вращающегося барабана — центрифуги — плохо уложено, машина начинает дрожать и громыхать так, словно хочет превратиться в маленький автомобиль. Кто же толкает ее изнутри? Конечно же, центробежная сила, действующая со стороны сбившегося в ком белья. Приходится ее укрощать — останавливать машину и укладывать белье более равномерно. Хорошо еще, что центрифуга вращается не слишком быстро: 300-500 об/мин, поэтому ее можно остановить одним нажатием кнопки. А ведь в технике мы то и дело сталкиваемся со значительно большими скоростями вращения и огромными вращающимися массами. Тогда неуравновешенные центробежные силы могут причинить серьезный вред. Они вызывают вибрацию, увеличивают трение и износ подшипников. В результате машина быстро выходит из строя. В некоторых случаях центробежная сила может вообще не позволить валуна брать нужную скорость вращения.

Проведем маленький эксперимент: возьмем микроэлектродвигатель и присоединим его контакты к полюсам батарейки. Прислушайтесь к тоненькому жужжанию вращающегося ротора: его угловая скорость — около 70 об/с. А теперь попробуем снабдить мотор маховиком. Для начала грубо, от руки вырежьте из ластика колесико, на глаз наметьте карандашом его центр и небольшим усилием насадите на вал. Включим двигатель. Чувствуете, как забился он у вас в руке, как изменился звук по сравнению с прежним? Он стал гораздо ниже, потому что скорость вращения ротора снизилась в 5-10 раз. Всему виной неуравновешенная центробежная сила, создаваемая резиновым маховиком.

Теперь понятно, для чего бороться с центробежными силами. Как же от них избавиться — вернее, от их нежелательного действия?

Уравновешивание центробежных сил, приложенных к вращающемуся телу, называется в технике балансировкой. Простейший пример балансировки — укладка белья в центрифуге стиральной машины.

ПОГОНЯ ЗА ВРАЩАЮЩИМСЯ ВЕКТОРОМ

К сожалению, в огромном большинстве случаев балансировка — дело куда более сложное. Теория балансировки роторов была разработана сравнительно недавно — в 1935 году — замечательным ученым, механиком и кораблестроителем А. Н. Крыловым, рассказ о котором вы читали в «ЮТ» № 3 за 1983 год. Давайте познакомимся с основами этой теории.

Пусть небольшое тело массы m (материальная точка) вращается но окружности, совершая n оборотов в минуту. В механике скорость вращения принято измерять углом поворота за одну секунду; эта величина называется угловой скоростью и обозначается греческой буквой ω (омега). В одной минуте — 60 с, в одном обороте — 2Pi радиан, поэтому ω = 2Pi*n/60=0,1 n.

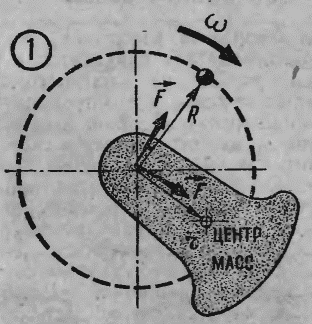
Обозначим через R вектор, направленный от оси к вращающемуся телу. Его длина равна радиусу окружности вращения, поэтому R называют радиус-вектором (рис. 1).

Оказывается, вектор центробежной силы F получается умножением радиус-вектора на массу тела и на квадрат угловой скорости: F=m*ω 2 *R (понятно, что векторы F и R направлены одинаково). Согласно III закону Ньютона такую же величину, но противоположное направление имеет центростремительная сила, приложенная к вращающемуся телу и удерживающая его на окружности. Если тело не может быть представлено как материальная точка (таково большинство тел), центробежная сила вычисляется в точности так же, но вместо R берется r — радиус-вектор центра масс тела (рис. 1).

Центр масс — это точка, в которой как бы сосредоточена вся масса тела. У симметричных тел (например, цилиндра или шара) центр масс совпадает с центром симметрии. Однако изготовить идеально симметричное тело невозможно, поэтому положение центра масс никогда точно не известно. Именно из-за этого возникает необходимость в балансировке вращающихся тел.

Произведение двух сомножителей — радиус-вектора центра масс и массы тела — принято называть вектором дисбаланса или просто дисбалансом: d=m*r. Дисбаланс измеряется в кг*м. Он обращается в нуль только тогда, когда ось вращения проходит через центр масс. При вращении тела вектор дисбаланса вращается вместе с ним. так что его направление совпадает с центробежной силой.

Вернёмся к нашему опыту с маховиком и попробуем рассчитать дисбаланс и центробежную силу. Пусть масса маховика m=30г, а расстояние от оси до центра масс r=2 мм. Величина дисбаланса составляет в этом случае 0,002*0,03=6*10 -5 кг. Казалось бы, очень немного. Но предположим теперь, что ротор вращается со скоростью 4500 об/мин (именно такова скорость вращения обычного микроэлектродвигателя). Тогда ω=450 рад/с, и центробежная сила F=d*ω 2 =12Н. Такая нагрузка непомерно велика для микродвигателя: сила трения в подшипниках вообще не даст ротору вращаться. Даже с таким маленьким маховиком, если он разбалансирован, микродвигатель не способен набрать своей номинальной скорости!

Какое значение дисбаланса допустимо, а какое нет, зависит главным образом от конструкции и скорости вращения ротора. Тихоходная гидравлическая турбина массой в десятки тонн без малейшего ущерба может иметь дисбаланс величиной 10 кг*м, а вот газовой турбине, для которой и 30 тыс. об/мин не предел, даже 10 -6 кг*м — многовато.

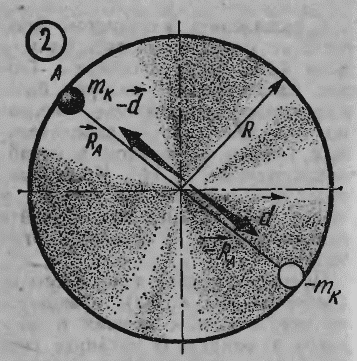
Посмотрите на рисунок 2. Здесь изображено колесо радиуса R с дисбалансом d. Допустим, что мы можем размешать дополнительные корректирующие грузы на ободе колеса, например налеплять пластилиновые шарики. Тогда компенсировать дисбаланс очень просто: достаточно поместить в точке А кусочек пластилина массы mk=d/R. B самом деле, теперь дисбаланс колеса будет равен нулю: d=d+R_A*d/R=d-d. Заметим, что радиус R можно выбрать любым, но при этом будет меняться и масса корректирующего груза. И наоборот, если задана масса m’_k>=d/R, то дополнительный груз нужно разместить на расстоянии d/m’_k от центра.

Присмотритесь повнимательнее к колесам легковых автомобилей. На ободах некоторых из них вы увидите небольшие овальные грузики. Теперь вам должно быть понятно их назначение. Чаще, однако, корректирующие массы не добавляют, а изымают. Ведь добавление груза массы m_k в точку с радиус-вектором R_A равносильно изъятию груза той же массы в диаметрально противоположной точке (-R_A) (рис. 2). В технике часто так и поступают: в нужной точке высверливают неглубокое отверстие, не нарушающее прочности балансируемой детали, убирая тем самым требуемую массу. Такие отверстия часто можно видеть на маховиках и роторах электродвигателей.

БАЛАНСИРОВОЧНЫЙ СТАНОК НА ВАШЕМ СТОЛЕ

Балансировать различные вращающиеся детали приходится вовсе не только на машиностроительных заводах и в авторемонтных мастерских. С такой задачей вполне может столкнуться в своей работе каждый юный техник или моделист. Во многих моделях присутствует маховик. Это очень полезная деталь: маховик способен сглаживать неравномерность работы двигателя. Неуравновешенный маховик, напротив, вызовет сильную вибрацию и не даст мотору набрать обороты. Всеми достоинствами маховика можно пользоваться, лишь тщательно его отбалансировав.

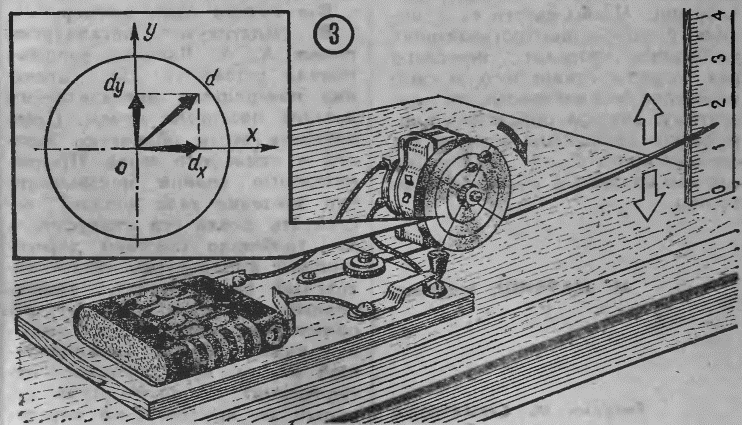
В этом вам поможет простой станок, который мы предлагаем вашему вниманию. Он представляет собой плоскую, закрепленную с одного конца пружину, на которой установлен микродвигатель с балансируемым маховиком (рис. 3). В качестве пружины можно взять контактную пластину от старого реле. К ее концу следует прикрепить длинную и легкую лучинку или соломинку с заостренным концом.

Включите мотор: тотчас же начнется вибрация, о величине которой сообщит размах колебаний острия соломинки. Для его измерения поместите возле острия прозрачную линейку с миллиметровой шкалой. По мере раскручивания двигателя этот размах будет то возрастать, то снова убывать. Возможно, что при максимальных оборотах острие окажется почти неподвижным. Не потому, конечно, что центробежная сила исчезла: просто чувствительность пружины к высокочастотной вибрации сравнительно невелика. По этой причине измеряют наибольший размах колебаний острия «на выбеге» — во время торможения двигателя после отключения питания. Длину соломинки, толщину пружины и место установки на ней двигателя необходимо подобрать так, чтобы размах был как можно большим, тем самым выше будет чувствительность вашего прибора.

Итак, величина дисбаланса измеряется размахом колебании острия соломинки. Разумеется, мы не знаем, какая величина дисбаланса точно соответствует, скажем, размаху в 7 мм (у нашего прибора нет проградуированнои шкалы), но можем сказать с уверенностью, что чем больше размах, тем больше и дисбаланс.

Теперь нужно запастись пластилином и приступить к балансировке. Однако прежде наметим план «погони» за вектором дисбаланса. Представим его в виде суммы проекций на две перпендикулярные оси: d=d_x+d_y (рис. 3). Эти оси (ОХ и ОУ) следует начертить на маховике совершенно произвольно до начала балансировки. Будем компенсировать составляющие дисбаланса по очереди: сперва d_x, потом d_y. Поместив корректирующий груз в любой точке А на оси ОХ, мы не изменяем составляющую d_y — ведь OA перпендикулярна ОУ; изменяться будет только d_x. Перемещая кусочек пластилина по оси ОХ, найдите такое его положение, при котором размах острия (а вместе с ним и дисбаланс) наименьший. Если эта точка окажется вблизи от обода маховика, возьмите кусочек побольше; если вблизи от центра — поменьше. Только учтите, что перемещать пластилиновый грузик нужно, не снимая маховик с оси. Вообще, если после начала балансировки вы почему-либо измените положение маховика на оси, балансировку придется начинать сначала.

Добившись минимального размаха движений соломинки, возьмите другой кусочек пластилина и повторите ту же самую процедуру, только теперь с осью ОУ (первый грузик, конечно, должен оставаться на своем месте). Тем самым вы, не изменяя составляющей дисбаланса d_x, уменьшите, насколько это возможно, составляющую d_y. Поскольку общий дисбаланс d=(d_x 2 +d_y 2 ) 0.5 , в результате он может быть совершенно ликвидирован.

Фактически, однако, ни d_x, ни d_y не компенсируются с абсолютной точностью, поэтому нельзя ожидать полного исчезновения вибрации. Чтобы свести ее к минимуму, коррекцию составляющих дисбаланса проводят несколько раз подряд. Кроме того, и само измерение можно произвести по-другому: сначала определить направление дисбаланса, а затем уж скомпенсировать его. Подумайте, как это сделать, а потом напишите нам.

М. МАРКИШ, инженер
Рисунки М. СИМАКОВА

Источник

Центробежная сила

Центробежная сила , общее название , но не так с центробежным эффектом , является фиктивной силой , которая появляется естественным в контексте изучения движения объектов в хранилищах не инерциальной . Ощущаемый эффект возникает из-за вращательных движений этих систем отсчета и приводит к тенденции отодвигать тела от центра вращения. Одним из примеров является чувство катапультирования, которое испытывает путешественник в автомобиле, совершающем поворот.

Резюме

Исторический

Выражение центробежной силы ( по- латыни vis centrifuga ) было открыто Христианом Гюйгенсом в 1659 году, задолго до того , как Исаак Ньютон сформулировал фундаментальный принцип динамики и четко определил общее понятие силы . Открытые им теоремы были опубликованы в 1673 году в качестве приложения к его « часам осциллятора» . Мемуары 1659 года были опубликованы только в 1703 году, примерно через десять лет после его смерти.

Со времен Галилея мы знаем, что тела падают в свободном падении с равномерно ускоренным движением. С точки зрения Гюйгенса, тело притягивает проволоку, которая удерживает ее, когда это тело стремится двигаться в направлении протяжения проволоки с равномерно ускоренным движением. По его словам, это правило применяется не только к тяжелому телу, но и к телу, вращающемуся по кругу на конце проволоки вокруг фиксированной точки. В последнем случае сила тяги, оказываемая на проволоку, противодействует центробежной силе, которая в случае разрыва проволоки отодвигает тело от его круговой траектории, заставляя его следовать по прямолинейной траектории, касательной к окружности. Относительно круга, когда проволока обрывается, расстояние между точкой, занимаемой телом на касательной, и точкой, которую оно занимало бы на окружности, увеличивается при равномерно ускоренном движении. Затем сравнение со свободным падением позволяет Гюйгенсу определить выражение центробежной силы по отношению к весу. В нем, в частности, говорится, что:

• Утверждение I: при постоянной угловой скорости центробежная сила пропорциональна радиусу окружности;
• Предложение II: при постоянном радиусе оно пропорционально квадрату скорости;
• Утверждение V: центробежная сила движущегося тела, пересекающего круг со скоростью, равной скорости, полученной в конце свободного падения на четверть диаметра, равна его весу.

В современных обозначениях утверждение V гласит, что если R — радиус круговой траектории, и если v — скорость, полученная в конце свободного падения с высоты R / 2, (т.е. где g — это l ‘ускорение свободного падения ), то центробежное ускорение равно г либо . Утверждения I и II утверждают, что центробежное ускорение есть во всех случаях. v знак равно р грамм <\ displaystyle v = <\ sqrt >> v 2 / р <\ displaystyle v ^ <2>/ R> v 2 / р <\ displaystyle v ^ <2>/ R>

Выражение силы фиктивное появляется у Кориолиса в 1844 году.

Выражение центробежной силы

Это напрямую связано с классической кинематикой и тремя законами движения Ньютона . Его интенсивность определяется формулой:

F cen знак равно м ⋅ ω 2 ⋅ р знак равно м ⋅ v 2 р . <\ displaystyle _ <\ textrm > = m \ cdot \ omega ^ <2>\ cdot R = <\ frac > > \;.>

Эти два эквивалентных отношения действительны в Международной системе единиц со следующими обозначениями и единицами ( при необходимости конвертируйте единицы ):

• F cen <\ displaystyle \ scriptstyle _ <\ textrm >>центробежная сила в ньютонах (Н), где 1 ньютон близок к 0,1 килограмм-силе;
• m — масса рассматриваемого объекта в килограммах (кг);
• ω — угловая скорость в радианах в секунду (рад / с), поэтому 1 оборот в секунду = 6,28 рад / с и 1 оборот в минуту = 0,105 рад / с;
• v — линейная скорость по касательной к пути в метрах в секунду (м / с), 1 м / с соответствует 3,6 км / ч;
• R — расстояние от оси вращения до центра тяжести объекта, то есть радиус кривизны пути в метрах (м).

Центробежная сила может быть представлена вектором, перпендикулярным мгновенной оси вращения .

Центробежная сила и ускорение

Центробежная сила и вес, действующие на объект массы m, — это две силы, которые пропорциональны m (согласно принципу эквивалентности ). Кроме того, часто бывает более выразительным рассматривать не силы F, а ускорения F / m .

Ускорение — это кинематическая величина, единицей СИ является метр в секунду в квадрате (м / с 2 ).

Также можно использовать число g , определяемое соотношением между рассматриваемым ускорением и ускорением свободного падения , которое составляет приблизительно 9,81 м / с 2 .

Таким образом, на обыденном языке число g составляет десятую часть значения ускорения, выраженного в м / с 2 .

Порядки величины центробежных ускорений

В зависимости от скоростей (линейных или угловых) и радиусов кривизны R численный расчет дает приблизительно [ см. желаемый] :

Примеры

Автомобиль в повороте

Это неизбежно для вращающихся систем, но может доставлять неудобства пассажирам транспортного средства, меняющим направление движения. Затем они чувствуют центробежную силу, выталкивающую их из поворота. Согласно основному принципу динамики , сиденье втягивает пассажира внутрь, иначе пассажир не повернется вместе с автомобилем. Действительно, это ощущение связано с инерцией (способностью любого материального тела противостоять навязанному движению). Предмет, помещенный на приборную панель, скользит по направлению к внешней стороне автомобиля в повороте, при этом сцепление с приборной панелью оказывается недостаточным, чтобы заставить ее следовать за поворотом; объект фактически уходит прямо (следовательно, наружу для наблюдателя, находящегося в автомобиле). Внешний наблюдатель увидит траекторию, касательную к траектории поворота транспортного средства, а не радиальную траекторию в направлении так называемой центробежной силы.

Для компенсации этого эффекта мы прибегаем к устройствам: комбинация противодействующих перегрузок пилотов истребителей , система наклона некоторых поездов , наклонные повороты дорог, наклон транспортных средств с менее чем четырьмя колесами в поворотах (велосипеды, мотоциклы и двухколесные самокаты, трехколесные самокаты, оснащенные системой гидравлического опрокидывания ).

Отжать белье

Вращательное движение, прикладываемое к белью барабаном стиральной машины, вызывает ускорения, которые также передаются частицам воды. Пока они оставались застрявшими в состоянии покоя, из-за капиллярного воздействия на ткань силы сцепления становятся недостаточными, когда узел вращается достаточно быстро. Локальное равновесие больше не гарантируется, и вода выбрасывается.

Разделение жидкости

Элементы, составляющие гетерогенные жидкости, такие как кровь , разделяются по тому же принципу ультрацентрифугированием . Силовое поле , индуцированное центробежный эффект похоже на более сильное гравитационное поле , которое благоприятствует осаждение из фаз из различных плотностей .

Центробежные регуляторы (на старых паровых машинах)

На схеме ниже воспроизводится принцип работы регулятора Джеймса Ватта . Приводимый машиной через ремень, ротор видит, как его вес удаляется. Затем рычажный механизм управляет клапаном. Воздействие на клапан оказывает обратное влияние на мощность, подаваемую на машину, что позволяет управлять системой. Независимо от того, закрывается ли клапан слишком быстро или слишком медленно, система в конечном итоге находит баланс и, следовательно, регулируемую скорость.

Источник