Что значит указать наименьшее значение функции

Как найти наименьшее значение функции на отрезке: правила, примеры и особенности

Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.

Что такое значение функции?

Вам будет интересно: Проверочное слово к слову «скворец», корень и лексическое значение

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.

Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?

Как можно найти наименьшее значение функции, используя график функции?

Вам будет интересно: Горизонтальный перенос генов: основы генетики, история открытия, принцип действия и примеры

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.

Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.

О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:

1) Найти и отметить концы этого отрезка.

2) Визуально определить, какая точка на этом отрезке лежит ниже всего.

3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.

Точки экстремума на графике производной. Где искать?

Вам будет интересно: Покои — это многозначное слово. Что именно оно означает?

Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.

Итак, производная — это мгновенная скорость возрастания функции. Согласно геометрическому определению производная соответствует угловому коэффициенту касательной, которая непосредственно проведена к данной точке.

Известно, что в точках экстремума касательная параллельна оси Ox. Это значит, что ее угловой коэффициент — 0.

Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.

Если производная из положительной становится отрицательной — это точка максимума. Если из отрицательной становится положительной — точка минимума.

Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.

Как находить точки экстремума с помощью производной?

Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.

Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:

• Найти производную от функции.
• Приравнять ее к нулю.
• Найти корни уравнения.
• Проверить, являются ли полученные точки точками экстремума или перегиба.

Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.

• Применив теоремы, определить какие точки являются точками минимума, а какие – максимума.

Вычисление наименьшего значения функции с применением производной

Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?

Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.

Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.

Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.

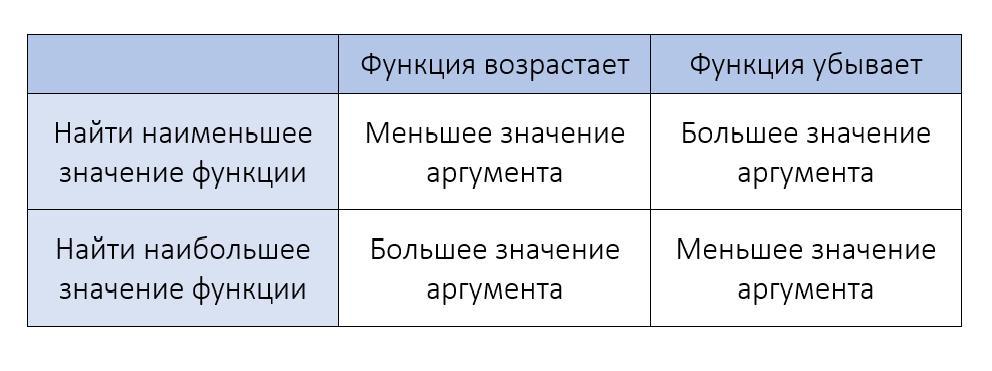
Что делать, если на данном отрезке отсутствуют точки минимума?

Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?

Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.

1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.

В соответствии с ними подставить в функцию большее или меньшее значение аргумента.

2) Просто подставить в функцию обе точки и сравнить полученные значения функции.

В каких заданиях нахождение производной необязательно

Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.

Вершина параболы находится по формуле.

Если a 0, то ветви параболы направлены вверх, вершина – точка минимума.

Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.

2) Функция y = tg x. Или y = ctg x.

Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.

Основные типы заданий

Задание: наибольшее или наименьшее значение функции. Пример на графике.

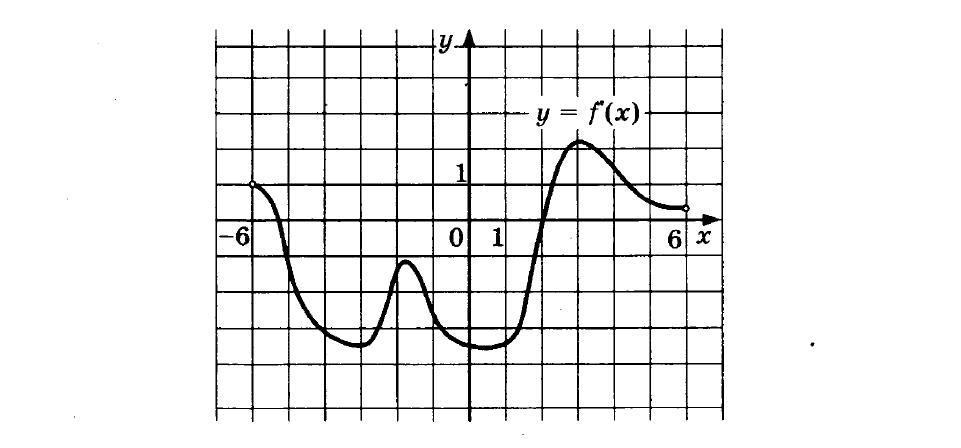
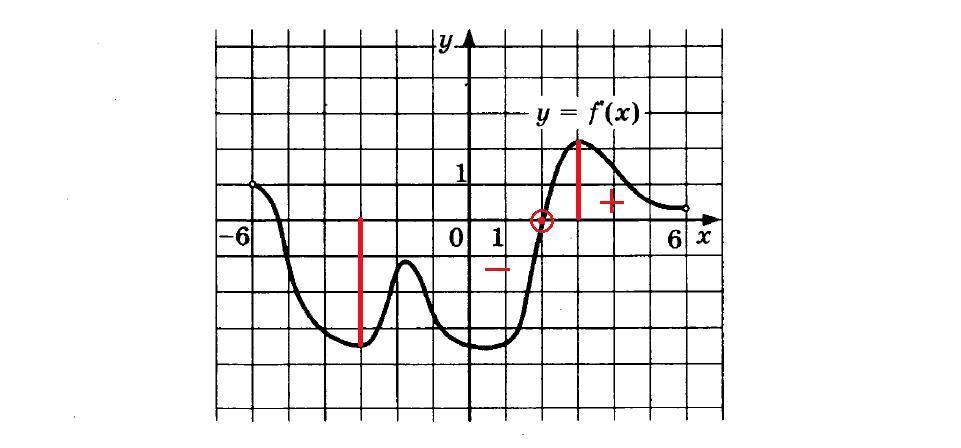
На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?

Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.

Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.

Найдите наименьшее значение функции y = (x — 8) ex-7 на отрезке [6; 8].

1. Взять производную от сложной функции.

y’ (x) = (x — 8) ex-7 = (x — 8)’ (ex-7) + (x — 8) (ex-7)’ = 1 * (ex-7) + (x — 8) (ex-7) = (1 + x — 8) (ex-7) = (x — 7) (ex-7)

2. Приравнять полученную производную к нулю и решить уравнение.

x — 7 = 0, или ex-7 = 0

x = 7; ex-7 ≠ 0, нет корней

3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.

y (6) = (6 — 8) e6-7 = -2e-1

y (7) = (7 — 8) e7-7 = -1 * e0 = -1 * 1 = -1

y (8) = (8 — 8) e8-7 = 0 * e1 = 0

Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.

Источник

Наибольшее и наименьшее значение функции

Теория к заданию 12 из ЕГЭ по математике (профильной)

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Проверить, какие стационарные точки входят в заданный отрезок.
4. Вычислить значение функции на концах отрезка и в стационарных точках из п.3
5. Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Разложить производную функции на множители.
4. Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
5. Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^, n∈N$
$<1>/$	$-<1>/$
$<1>/x<^n>, n∈N$	$-/>, n∈N$
$√^n, n∈N$	$<1>/>, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$<1>/$
$ctgx$	$-<1>/$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	$<1>/$
$log_x$	$<1>/$

Основные правила дифференцирования

1. Производная суммы и разности равна производной каждого слагаемого

Найти производную функции $f(x) = 3x^5 – cosx + <1>/$

Производная суммы и разности равна производной каждого слагаемого

Источник

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1 . Находим ОДЗ функции.

2 . Находим производную функции

3 . Приравниваем производную к нулю

4 . Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции 0″ title=»f^(x)>0″/>, то функция возрастает на этом промежутке.

Если на промежутке I производная функции , то функция убывает на этом промежутке.

5 . Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6 . Находим значение функции в концах отрезка,

• затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
• или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее — в левом: .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее — в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть и .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть и .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2.

3. , если или

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1 . Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2.

3.

Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

Ответ: 5.

2 . Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции /2+k, k» title=»x<>/2+k, k«/>

2.

Производная равна нулю при , однако, в этих точках она не меняет знак:

, следовательно, =3″ title=»3/>>=3″/>, значит, =0″ title=»3/>-3>=0″/>, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

=0″ title=»y^=3/>-3=<3-3cos^2>/>=<3sin^2>/>=3tg^2>=0″/>

Ответ: 5.

3 . Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции : /2+k, k» title=»x<>/2+k, k«/>

2.

3.

,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: и

Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки и производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

И.В. Фельдман, репетитор по математике.

Источник