- Третья часть — это сколько?
- Калькулятор процентов
- Примеры вычислений на калькуляторе процентов
- Как решать задачи с процентами
- Основные определения
- Типы задач на проценты
- Тип 1. Нахождение процента от числа
- Тип 2. Нахождение числа по его проценту
- Тип 3. Нахождение процентного отношения двух чисел
- Тип 4. Увеличение числа на процент
- Тип 5. Уменьшение числа на процент
- Тип 6. Задачи на простые проценты
- Тип 7. Задачи на сложные проценты
- Способы нахождения процента
- Деление числа на 100
- Составление пропорции
- Соотношения чисел
- Задачи на проценты с решением
Третья часть — это сколько?
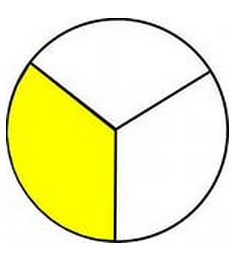
Третья часть — это одна часть из равных трех частей. Чтобы вычислить в процентах, необходимо проделать следующие действия: 100*1=100/3=33,33333%, для вычисления в числовом значении: 1/3=0,33333. Например, берем торт и делим на три одинаковых куска, один кусок — это одна третья всего торта.
Если в классе, к примеру, 30 человек учится, то третья часть от всего количества составит 10 человек. Если человеку нужно пройти 3 километра, то треть пути будет ровно один километр. Третья часть от килограмма — это 333,333 грамма. Ну и так далее.
Это один кусок из трёх одинаковых кусков.
Если в процентном соотношении, то третья часть — это 33,33 % от общего количества чего-то. Другими словами, целое нужно поделить на три равных части, одна из которых и будет называться третья часть.
Это смотря что измерять
если взять третью часть от полного угла, то это будет угол 120 градусов, одна треть от развернутого угла равна углу 60 градусов, а 1/3 прямого угла равна углу 30 градусов.
Если отмерять время, то здесь полезно знать, что треть месяца называется декадой и она равна 10 дням, а треть часа равна 20 минутам, треть минуты 20 секундам.
Если пройденный путь это треть от всего пути, то он всегда в два раза меньше того пути, который осталось еще пройти.
Если в десятичной системе, то треть равна 0,33(3), а если треть записать в виде правильной дроби. то она будет равна
1/3 = 2/6 = 3/9 = 4/12 и т.д.
Это если всё имеющееся количество разделить на 3 части, а потом взять одну из этих частей.
Если говорить о числах или количестве чего-то, что можно посчитать по штукам — нужно просто число/ количество штук разделить на три.
Если речь идет о чем-то, что штуками не измерить — например, «треть стакана — это сколько?» («1/3 стакана — это сколько?»)- то просто разделите на глаз и возьмите одну из частей. Так же можно посчитать 2/3 стакана: разделите стакан на глаз на три части и насыпьте/ налейте 2 из них.
Третью часть легко определить от числа делящегося на три например число 9:
Число 9 делим на три и получаем три- это и будет третья часть.
В круге 360 градусов и если поделить на три каждая часть будет составлять 120 градусов — это количество тоже является третью частью круга.
Третья часть или 1/3.
Если взять число и разделить его на три, это уже и будет третья часть.
Например, есть число 12. Третья часть от 12 (12 : 3 = 4) — это 4.
Если нас интересует третья часть не числа, а какого-нибудь вещества, например, муки в стакане, надо условно разделить стакан муки на три части и взять из них одну часть. Это и будет третья часть стакана муки.
Смотря третья часть чего именно. Третья часть — это какой-то предмет/вещь/цифра и т.д. деленная на три части и одна из этих частей как раз и будет третьей. Можно еще сказать, что это 33.33% чего-либо — так вроде немного понятнее становится.
Простите, а чего третья часть? Или опять нас поймать хотите?)
Я возьму ту величину, что мне ближе всего и скажу сколько будет. Например, сто килограммов. Третья часть будет примерно, тридцать три килограмма.
Третья часть — это одна часть одного целого, если это одно целое разделить на три равные части.
Если кусок теста разделить на 3 равные части, то одна такая часть — это третья часть.
Если разделить одно целое на 2, 4, 5, 6 частей, то получатся одна вторая, одна четвёртая (четверть), одна пятая и т.д.
Третья часть — это одна третья.
Третью часть ещё называют одна третья или треть.
Если записать математически, то это 1/3 или 0.3333333. .
А если пытаться понять, то тогда:
Попробуйте взять что-нибудь, что можно разрезать, например пирог.
Разрежьте пирог на три равные между собой части.
Возьмите в руку одну из отрезанных частей пирога.
Вы держите в руке одну третью часть пирога.
Решений предоставлено достаточно, но ответы не совпадают. Попробую решить эту задачу, так как это я понимаю. Все разговоры о плагиате, желающие высказаться, оставляють при себе.
Картинка к задаче не соответствует действительности. Дело в том, что если изображать шары в виде окружностей, то на виде с любой стороны параллелепипеда, они будут выглядеть, как две пересекающиеся окружности. Для того, чтобы увидеть касание окружностей их нужно рассматривать в плоскости перпендикулярной основанию и проходящей через центры шаров. В моем случае, это плоскость G-G.
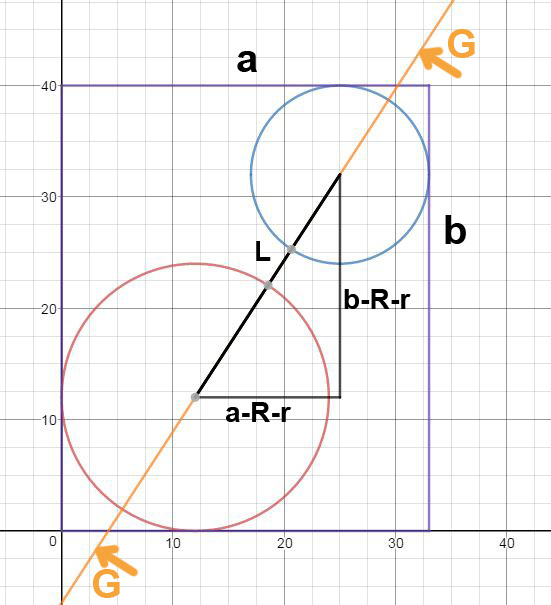
Возьмем коробку и шары произвольного размера. Разместим их в диагонально противоположных углах параллелепипеда. На виде сверху это будет выглядеть следующим образом. Где a и b ширина и длина коробки, соответственно.
По теореме Пифагора несложно посчитать размер между осями шаров, перпендикулярных основанию коробки (L).
Подставив в формулу значения из условия задачи, получим L=4sqrt(13)=14.422
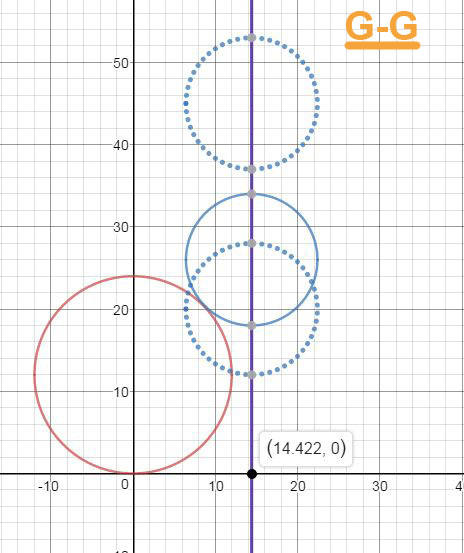
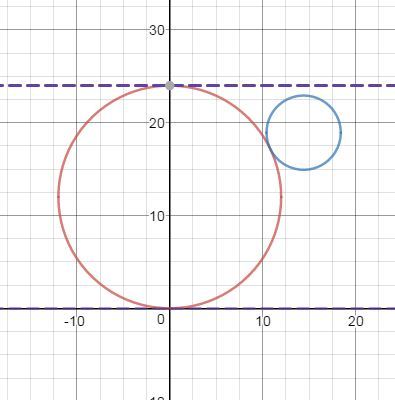
Далее рассмотрим картинку в плоскости G-G
Расстояния между осями определено. Большой шар условно неподвижен, а маленький может перемещаться по вертикали. Естественно, нас интересует только вариант, когда окружности соприкасаются в одной точке.
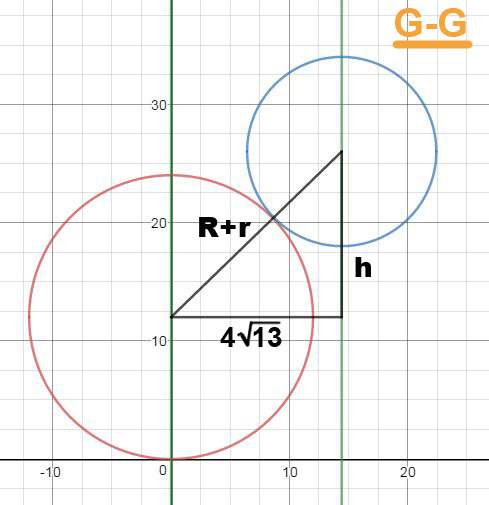
Рассмотрим эту схему подробнее.
Опять же, несложно по Пифагору определить расстояние между центрами шаров, по вертикали.
При подстановке значений получим h=6.928
И далее, высота коробки будет равна R+h+r=22.928 , по маленькому шару. Изобразим картинку в масштабе.
Очевидно, что маленький шар спокойно поместится в свободный угол коробки и не будет принимать участие в формировании высоты коробки. А это значит, что высота коробки будет принята по размеру большого шара, то есть:
Высота коробки будет равна 24.
Задача оказалась с подвохом.
Вычитанием называется двухместная операция, обратная сложению. Она не коммутативна и не ассоциативна, обладает антикоммутативностью. В случае, если на том же множестве определено ещё и умножение, то вычитание должно быть дистрибутивно по отношению к нему.
То есть, в арифметике у вычитания выделяют лишь 2 свойства:
- антикоммутативность (при перемене мест уменьшаемого и вычитаемого результат получатся обратным) [a-b=-(b-a)];
- дистрибутивность по отношению к умножению (распределительный закон) [a*(b-c)=ab-ac].
Ассоциативность и привычная по сложению коммутативность отсутствуют:
У умножения есть переместительное, сочетательное и распределительное свойство (которые чаше называются законами). Записываются они так (в том же порядке):
a*b = b*a (от перестановки сомножителей произведение не меняется — вообще говоря, это верно не для всех объектов, для которых определена операция «умножение». Скажем, для матриц или для элементов групп переместительное свойство не соблюдается).
Могу посоветовать сайт, которым пользуемся мы, когда ищем ответы по математике. Он называется слово, потом точка, потом домен ws (а не ru).
Там постранично отсканирован решебник, просто и понятно изложено. Вот выдержка именно из него:
Там есть и другие решебники, пригодятся ребенку позже.
Есть еще математикус.ру.
Есть сайт алленг.ру, там можно помимо готовых домашних заданий найти учебники (в том числе и для высшего и средне-профессионального образования), их количество постоянно пополняется.
Источник
Калькулятор процентов
Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой
Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.
Калькулятор разработан специально для расчета процентов. Позволяет выполнять разнообразные расчеты при работе с процентами. Функционально состоит из 4-х разных калькуляторов. Примеры вычислений на калькуляторе процентов смотрите ниже.
| ||
| Сколько составляет % от числа | ||
| 0% от числа 0 = 0 | ||
| Сколько % составляет число от числа | ||
| Число 0 от числа 0 = 0% | ||
| Прибавить % к числу | ||
| Прибавить 0% к числу 0 = 0 | ||
| Вычесть % из числа | ||
| Вычесть 0% из числа 0 = 0 | ||
|
Примеры вычислений на калькуляторе процентов
Какое число соответствует 23 % от числа 857 ?
Итог — 197.11
Как вычислять:
Получаем коэффициент — 857 / 100% = 8.57.
Получаем итоговое число — 8.57 x 23% = 197.11
Сколько процентов составляет 24 от числа 248 ?
Итог — 9.677 %
Как вычислять:
Получаем коэффициент — 248 / 24 = 10.333
Получаем проценты — 100% / 10.333 = 9.677 %
Прибавить 35% к числу 487 ?
Итог — 657.45
Как вычислять:
Получаем коэффициент — 487 / 100 = 4.87
Получаем число равное 35% — 4.87 x 35 = 170.45
Получаем итоговое число — 170.45 + 487 = 657.45
Вычесть 17% из числа 229 ?
Итог — 190.07
Как вычислять:
Получаем коэффициент — 229 / 100 = 2.29
Получаем число равное 17% — 2.29 x 17 = 38.93
Получаем итоговое число — 229 — 38.93 = 190.07
Источник
Как решать задачи с процентами
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
А вот, как перевести проценты в десятичную дробь — обратным действием:
Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
38/0,16 = 38 * 100/16 = 237,5
Значит 237 задачи включили в этот сборник.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: возьмем алгоритм из правила выше:
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
В классе учится 10 девочек — это 40%.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
Формула расчета процента от числа выглядит так:
a = b * ((1 + c) / 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?
Как решаем: подставим в формулу данные из условий задачи.
110 * (1 + 12/100) = 110 * 1,12 = 123,2.
Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
Формула расчета выглядит так:
a = b * ((1 — c) / 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Как решаем: подставим в формулу данные из условий задачи.
100 * (1 – 25/100) = 75
75 выпускников закончат школу в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а * ((1 + у * х)/ 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?
Как решаем: подставим в формулу данные из условий задачи.
5000 * (1 + 12 * 15/100) = 14000
Родители через год внесут в банк 14000 рублей.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
S = а * ((1 + х)/100) y ,
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.
Как решаем: просто подставим в формулу данные из условий задачи:
25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Способы нахождения процента
Универсальная формула для решения задач на проценты:
| A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число. |
Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.
Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.
Деление числа на 100
При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
Ответ: выгоднее воспользоваться скидкой 15%. Составление пропорцииПропорция — определенное соотношение частей между собой. С помощью метода пропорции можно рассчитать любые %. Выглядит это так: Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение. Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Ответ: купить спортивную футболку выгоднее на 194,6 рубля. Соотношения чиселЕсть случаи, при которых можно использовать простые дроби.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Ответ: средств хватит, так как пиджак стоит 6375 рублей. Задачи на проценты с решениемКак мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ. Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг? 76 : 100 = 0,76 — 1% от массы человека Ответ: масса воды 53,2 кг Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой? Обозначим первоначальную цену товара через х. После первого понижения цена станет равной. Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим: 0,6х — 0,25 * 0,6x = 0,45x После двух понижений изменение цены составит: Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%. Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто? По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто Получается, что стоимость одной пары брюк — это 23% стоимости пальто. Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто. Ответ: пять пар брюк на 15% дороже, чем одно пальто. Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены. По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27. Ответ: заработок жены составляет 27%. Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги? Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги. Источник |


 Добавить в Избранное
Добавить в Избранное 




