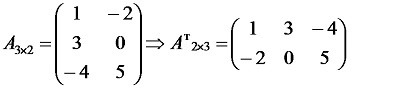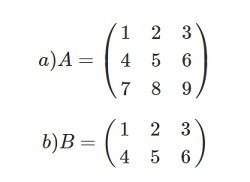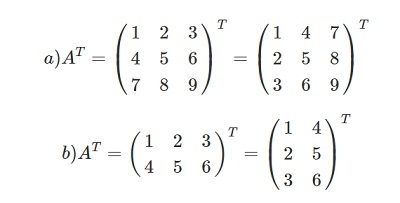Что значит транспонировать матрицу кратко

Транспонирование матрицы

Обновлено: 19 Июля 2021

Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.

Что такое транспонированная матрица, в чем отличие от обычной

Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.

Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.

Особенности, определитель и свойства целочисленных

Свойства транспортирования целочисленных матриц:

• (A T ) T = A;
• (k · A) T = k · AT;
• (A + B) T = A T + В T ;
• (A · B) T = В T · A T

Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A T = det A.

Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.

Формула, как обозначается транспонированная матрица

Если исходная матрица обозначается как А, то у транспортированной будет обозначение A T .

Тогда формула для транспортировки выглядит следующим образом:

A T ij = A ji

Формально, если А = m × n, то A T = n × m, но математически это записывается через индексы i и j.

Примеры задач на транспонирование матриц

Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.

Задача: даны А = (m × n) и В = (m × n).

Необходимо выполнить транспортирование.

Произведение и сумма транспонированных матриц

Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.

В математическом виде теорема выглядит так:

С T = (A · B) T = В T · А T

Сумма вычисляется по аналогичной формуле:

C T = (A + B) T = A T + В T

Периодически возникают сложности с учебой? ФениксХэлп может помочь!

Источник

Как транспонировать матрицу в Python

Сегодня мы хотим разобрать, как транспонировать матрицу в Python. Однако сначала давайте рассмотрим, что представляет из себя матрица сама по себе и в чём заключается процесс транспонирования.

Итак, матрица состоит из строк и столбцов. Создать матрицу можно по-разному, но самый простой способ – использовать вложенные списки, как показано ниже:

Внутренние списки представляют собой строки, а каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца, т.е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.

Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Теперь давайте обсудим различные методы транспонирования матрицы.

Метод 1. Транспонирование матрицы с помощью NumPy transpose()

Первый метод, который мы разберем, — это использование библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать метод transpose() .

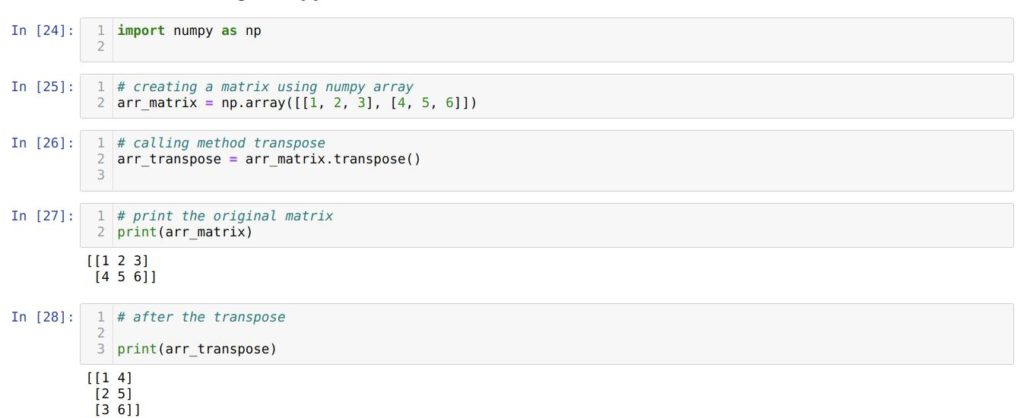
Давайте разберем всё по порядку. Для начала нам нужно импортировать модуль NumPy как np .

Дальше, в ячейке номер [25] мы создаем массив NumPy с именем arr_matrix .

В ячейке номер [26] мы вызываем метод transpose() для нашей матрицы – объекта arr_matrix , который мы создали ранее.

В ячейке номер [27] мы выводим на экран исходную матрицу arr_matrix .

А в ячейке номер [28] – транспонированную матрицу arr_transpose . Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.

Метод 2. Использование метода numpy.transpose()

Мы также можем транспонировать матрицу в Python с помощью numpy.transpose() . При этом мы передаем матрицу в метод transpose() в качестве аргумента.

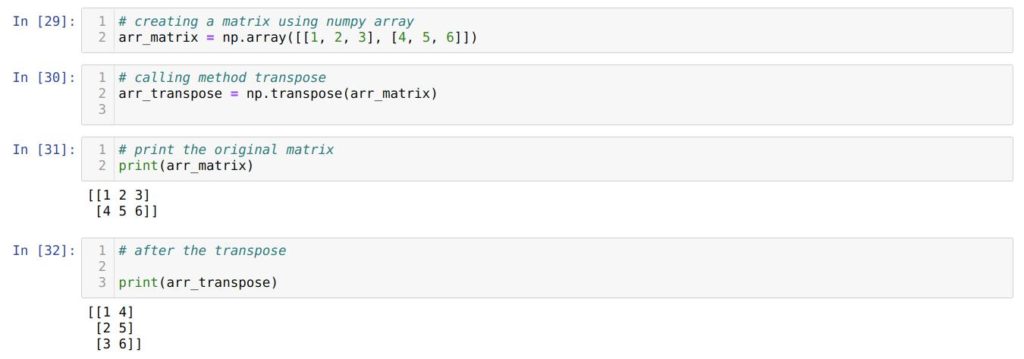
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именем arr_matrix .

Далее мы передаем arr_matrix в метод transpose() и сохраняем результат в новую переменную arr_transpose .

В ячейке номер [31] мы печатаем исходную матрицу arr_matrix .

А дальше мы выводим на экран транспонированную матрицу arr_transpose . Получаем результат аналогичный тому, что получили в первом примере.

Метод 3. Транспонирование матрицы с использованием библиотеки SymPy

Применение библиотеки SymPy – это еще один подход к транспонированию матрицы. Эта библиотека использует символьную математику для решения алгебраических задач.

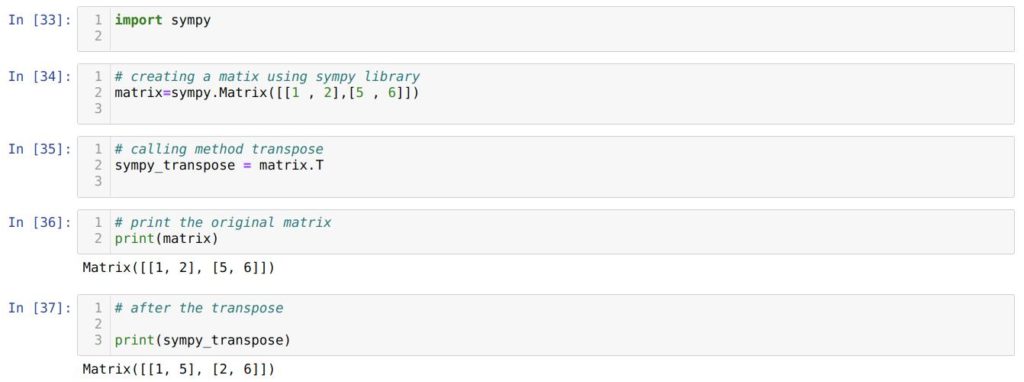
Сначала нам, конечно же, нужно импортировать библиотеку SymPy. Она не поставляется вместе с Python по умолчанию, поэтому вы должны установить её в своей системе, иначе код не будет работать.

В ячейке номер [34] мы создаем матрицу с помощью библиотеки sympy.

Дальше, в ячейке [35], мы вызываем transpose (T) при помощи точечного оператора и сохраняем результаты в новую переменную sympy_transpose .

В ячейке номер [36] мы печатаем исходную матрицу matrix . А в ячейке номер [37] – транспонированную матрицу sympy_transpose . Как видим, у нас получилась транспонированная матрица.

Метод 4. Транспонирование матрицы с использованием вложенного цикла

В Python матрицу можно транспонировать и без применения каких-либо библиотек. Для этого нам придется использовать вложенные циклы.

Мы создаем одну матрицу, а затем вторую (того же размера, что и первая) — для сохранения результатов после транспонирования. При этом важно отметить, что мы далеко не всегда знаем размерность исходной матрицы. Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.

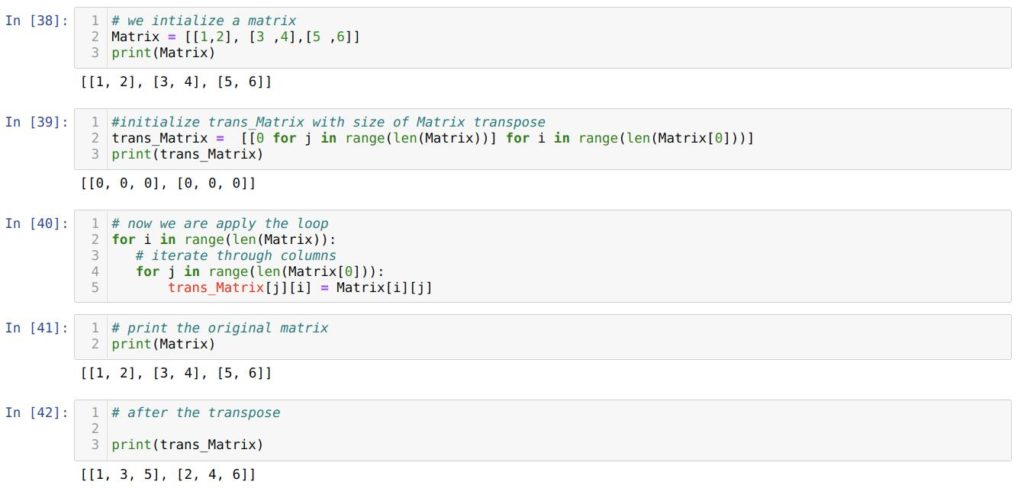
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.

В следующей ячейке мы применяем «питонический» способ узнать размерность транспонированной матрицы, используя исходную. А именно — используем генератор списков со вложенными циклами for .

В ячейке [40] мы запускаем два цикла for . Внешний цикл предназначен для строк, а вложенный – для столбцов.

В ячейке номер [41] мы выводим исходную матрицу Matrix . А в ячейке [42] — транспонированную матрицу trans_Matrix .

Метод 5. Использование генератора списка

Следующий метод, который мы разберем, — это использование генератора списка. Этот метод похож на предыдущий с использованием вложенных циклов, но он более «питонический». Можно сказать, что это более продвинутый способ транспонирования матрицы в одной строке кода без использования библиотек.

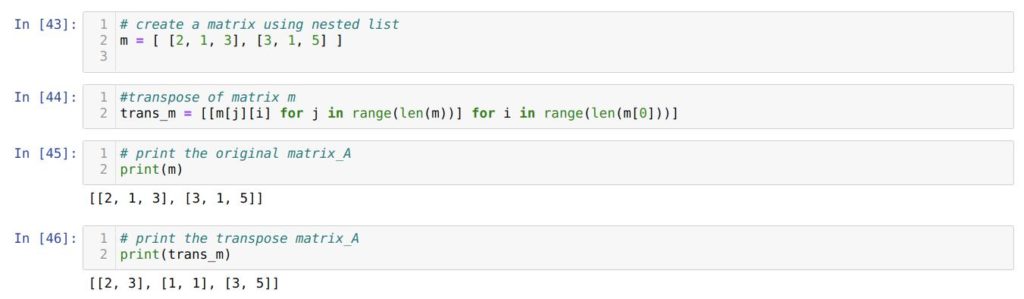
Сначала мы создаем матрицу m , используя вложенные списки.

Затем в ячейке номер [44] мы используем вложенные циклы, как и в предыдущем примере. Однако здесь мы делаем это в одну строчку, используя генератор списков. Более того, тут нет никакой необходимости менять индексы [j] [i] местами, как мы это делали в предыдущий раз.

В следующей ячейке мы выводим исходную матрицу m . После этого в ячейке номер [42] выводим транспонированную матрицу trans_m . Как видим, желаемый результат получен.

Метод 6. Транспонирование матрицы с помощью pymatrix

Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.

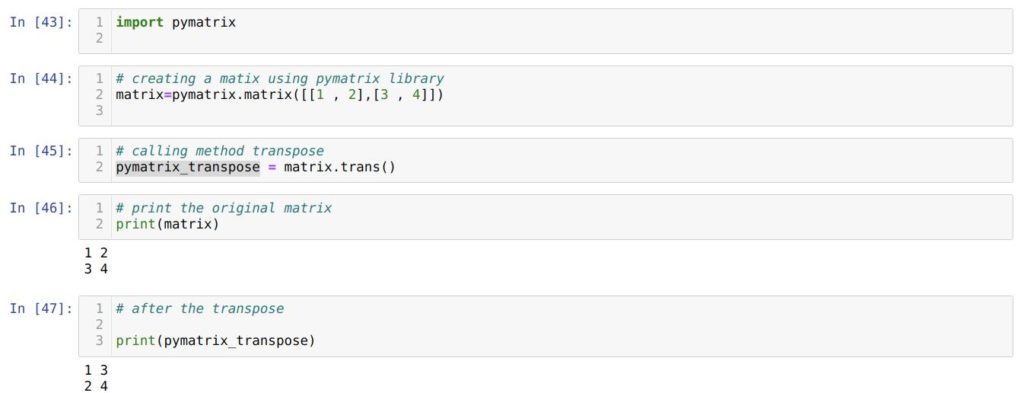
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется вместе с Python по умолчанию, поэтому, чтобы код работал корректно, нужно установить ее в своей системе перед использованием.

Затем при помощи библиотеки pymatrix мы создаем матрицу (в ячейке [44]).

В ячейке номер [45] вызываем метод trans() для нашей матрицы и сохраняем результаты в новую переменную pymatrix_transpose.

Потом мы выводим на экран исходную матрицу matrix . А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose . Как видим, код отработал правильно.

Метод 7. Использование метода zip

Zip – еще один метод транспонирования матрицы.

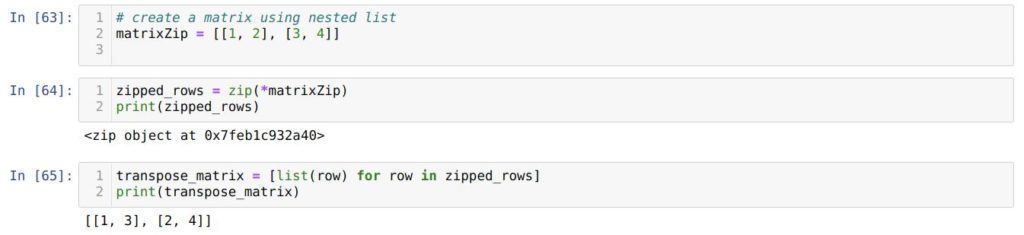
В ячейке номер [63] мы создаем новую матрицу, используя вложенные списки.

В ячейке номер [64] мы передаем матрицу в zip с помощью оператора * . Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей.

Заключение

Итак, сегодня мы рассмотрели, как транспонировать матрицу в Python. Мы разобрали различные методы, которые могут помочь нам в транспонировании матрицы (с использованием библиотек и без них).

Мы также познакомились с несколькими новыми библиотеками, такими как pymatrix и sympy.

Надеемся, теперь у вас не осталось вопросов о том, как транспонировать матрицу. Более того, вы можете выбрать наиболее подходящий способ для решения этой задачи.

Источник

Транспонированная матрица

Транспонированная матрица — матрица , полученная из исходной матрицы заменой строк на столбцы.

Формально, транспонированная матрица для матрицы размеров — матрица размеров , определённая как A T [i, j] = A[j, i].

и

Свойства транспонированных матриц

• 

Дважды транспонированная матрица А равна исходной матрице А.

• 

Транспонированная сумма матриц равна сумме транспонированных матриц.

• 

Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.

• 

При транспонировании можно выносить скаляр.

• 

Определитель транспонированной матрицы равен определителю исходной матрицы.

Связанные определения

Симметрическая матрица — матрица, удовлетворяющая соотношению . Для того чтобы матрица А была симметрической, необходимо и достаточно, чтобы:

• матрица А была квадратной,
• элементы, симметричные относительно главной диагонали, были равны.

Антисимметрическая (кососимметрическая) матрица — матрица, удовлетворяющая соотношению . Для того чтобы матрица А была антисимметрической, необходимо и достаточно, чтобы:

• матрица А была квадратной,
• элементы, симметричные относительно главной диагонали, были равны по модулю и различны по знаку,

Отсюда следует, что элементы главной диагонали такой матрицы (могут) равняются нулю.

См. также

• Сопряжённо-транспонированная матрица

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Транспонированная матрица» в других словарях:

транспонированная матрица — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] транспонированная матрица Результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [aij],… … Справочник технического переводчика

Транспонированная матрица — [transposed matrix] результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [aij], то транспонированная по отношению к ней записывается [aji] … Экономико-математический словарь

ТРАНСПОНИРОВАННАЯ МАТРИЦА — матрица, получающаяся из данной (прямоугольной или квадратной) матрицы после замены строк, соответствующими столбцами. Обозначение транспонированной матрицы , где a ik=aki для любых i и k … Большой Энциклопедический словарь

транспонированная матрица — матрица, получающаяся из данной (прямоугольной или квадратной) матрицы А = ||aik|| после замены строк соответствующими столбцами. Обозначение транспонированной матрицы А = ||a ik||, где a ik = aki для любых i и k. * * * ТРАНСПОНИРОВАННАЯ МАТРИЦА … Энциклопедический словарь

транспонированная матрица — transponuotoji matrica statusas T sritis fizika atitikmenys: angl. transposed matrix vok. transponierte Matrix, f rus. транспонированная матрица, f pranc. matrice transposée, f … Fizikos terminų žodynas

ТРАНСПОНИРОВАННАЯ МАТРИЦА — матрица, получающаяся из данной (прямоугольной или квадратной) матрицы i=1, . . ., т, k=1, . . ., п, после замены строк одноименными столбцами, т. е. матрица где i=1, . . ., п, k=l, . . ., т. Число строк Т. м. равно числу столбцов матрицы А, а… … Математическая энциклопедия

ТРАНСПОНИРОВАННАЯ МАТРИЦА — матрица, получающаяся из данной (прямоуг. или квадратной) матрицы А= |aik| после замены строк соотв. столбцами. Обозначение Т. м. А = ||а ik||, где a ik= од для любых i и k … Естествознание. Энциклопедический словарь

Транспонированная матрица — (нем. transponieren перекладывать, от лат. transpono переставляю) Матрица, получающаяся из данной (прямоугольной или квадратной) матрицы А = II a ik II после замены строк соответствующими столбцами. Обозначение Т. м. A = II a ik II, где a … Большая советская энциклопедия

матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика

Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь

Источник