Как доказать теорему о свойстве точек, равноудалённых от прямой?
Первый — что они все лежат на прямой, параллельной данной, второй — что какая-то прямая параллельна данной, третий — что ни одна точка, не равноудалённая от данной прямой, не лежит на какой-то прямой. Проболела, не знаю, как решать. В инете ничего не нашла. Могу примерный рисунок показать. Что дано, не знаю полностью, знаю, что дана прямая, 5 точек, и все они равноудалены от прямой.
Блин, ошиблась.. . В начале описаны 3 пункта, которые нужно доказать.
Если точки равноудалены от данной прямой, то любые две из них (А и В) могут быть по разные стороны от данной прямой, и поэтому они не лежат на прямой, параллельной данной. Любая другая с ними точка С не лежит на прямой этих двух точек (А и В) . В противном случае, эти три точки не были бы равноудалёнными от прямой (При построении получаются три прямоугольных треугольника с одинаковым острым углом. Два из них равны, а третий не равен двум другим. Катеты трёх треугольников — это расстояния от точек до прямой, и они получаются неодинаковыми.
Если же известно, что все точки, равноудалённые от данной прямой, лежат по одну сторону от неё, то они все лежат на одной прямой, параллельной данной. И никакая точка, не равноудалённая от данной прямой, не будет лежать на одной прямой с данными точками. Это легко доказать. Выбираем две любые точки из данных. Опускаем перпендикуляры от них на данную прямую. Они параллельны между собой, т. к. перпендикулярны одной и той же прямой. Они равны по условию. Значит получается параллелограмм. Он содержит прямой угол, т. е. это — прямоугольник. В нём противолежащие стороны параллельны. Значит, прямая, проходящая через две данные точки, параллельна данной. Далее проводим через одну из этих точек и через любую третью из данных прямую. По предыдущему, она параллельна данной прямой. Она также совпадает с ранее построенной прямой (если бы это было не так, то через одну и ту же точку проходили бы две различные прямые, параллельные одной и той же прямой, что невозможно по пятому постулату Евклида. Если взять любую неравноудалённую точку, то проводя через неё и одну из данных точек прямую, а затем через каждую из этих точек — перпендикуляры к данной прямой, то в предположении, что неравноудалённая точка будет лежать на той же прямой (которая параллельна данной) , мы получили бы прямоугольник (две стороны параллельны по предположению, две стороны — как перпендикуляры к одной и той же прямой, есть прямой угол) . В нём противолежащие стороны (перпендикуляры) должны быть равны, а на самом деле они не равны, т. к. точки не равноудалены. Противоречие. Значит неравноудалённая точка не лежит с равноудалёнными на одной прямой.
Источник
Что значит точка удалена от прямой
ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК
Один из основных способов задания фигур на плоскости заключается в указании свойства, которому удовлетворяют точки этой фигуры.
Вспомним определение окружности. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, удаленных от данной точки на данное расстояние. Свойством здесь является удаленность от данной точки на данное расстояние.
Фигуры, состоящие из всех точек, удовлетворяющих заданному свойству, получили особое название «геометрические места точек». Таким образом, геометрическим местом точек называется фигура, состоящая из всех точек, удовлетворяющих заданному свойству или нескольким заданным свойствам.
Поясним смысл слов “всех точек, удовлетворяющих заданному свойству” в этом определении. Они означают, что все точки, принадлежащие фигуре, удовлетворяют заданному свойству, и наоборот, все точки, удовлетворяющие заданному свойству, принадлежат фигуре. Другими словами, точка принадлежит фигуре в том и только том случае, когда для нее выполняется заданное свойство.
Рассмотрим еще несколько геометрических мест точек.
Серединным перпендикуляром к заданному отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Выясним, каким геометрическим местом точек является серединный перпендикуляр.
Теорема. Серединный перпендикуляр к отрезку является геометрическим местом точек, одинаково удаленных от концов этого отрезка.
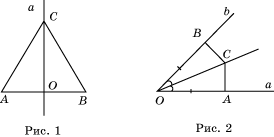
Доказательство. Пусть дан отрезок АВ и точка О – его середина. Покажем, что геометрическим местом точек, одинаково удаленных от точек А и В является серединный перпендикуляр к отрезку АВ (рис. 1). Действительно, очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру. Если точка С одинаково удалена от точек А и В и не совпадает с точкой О, то треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру. Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Теорема. Биссектриса угла является геометрическим местом точек, лежащих внутри данного угла и одинаково удаленных от его сторон.
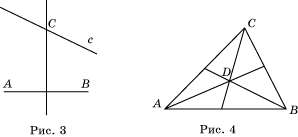
Доказательство . Рассмотрим угол c вершиной в точке О и сторонами а, b . Пусть точка С лежит внутри данного угла. Опустим из нее перпендикуляры СА и CB на стороны а и b (рис. 2). Если CA = CB , то прямоугольные треугольники А O С и В O С равны (по гипотенузе и катету). Следовательно, углы AOC и BOC равны. Значит, точка C принадлежит биссектрисе угла. Обратно, если точка C принадлежит биссектрисе угла, то прямоугольные треугольники AOC и BOC равны (по гипотенузе и острому углу). Следовательно, AC = BC . Значит, точка С одинаково удалена от сторон данного угла.
Пример 1. На данной прямой найдите точку одинаково удаленную от двух заданных точек.
Решение. Пусть c – данная прямая, A , B – данные точки (рис. 3). Геометрическим местом точек, одинаково удаленных от точек A и B, является серединный перпендикуляр к отрезку AB . Если серединный перпендикуляр и прямая c пересекаются, то искомой точкой C будет их точка пересечения. Если они не пересекаются, то задача не имеет решения.
Пример 2. Найдите точки, одинаково удаленные от прямых, на которых лежат стороны данного треугольника.
Решение. Рассмотрим треугольник ABC (рис. 4). Точка D этого треугольника одинаково удалена от AB и AC , если она принадлежит биссектрисе угла A . Аналогично, точка D треугольника ABC одинаково удалена от AB и BC , если она принадлежит биссектрисе угла B . Таким образом, точкой одинаково удаленной от AB , AC и BC будет точка пересечения биссектрис углов A и B треугольника ABC .
Заметим, что так как эта точка одинаково удалена от AC и BC , то она будет принадлежать и биссектрисе угла C . Значит, все три биссектрисы треугольника пересекаются в одной точке.
1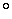 
. Какое геометрическое место точек представляет собой: а) отрезок; б) луч; в) круг c центром O и радиусом R ; г) кольцо с центром O и радиусами R 1 , R 2 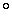( R 1 R 2 )?
2 
. Найдите геометрическое место центров окружностей, проходящих через две данные точки.
3 
. Найдите геометрическое место вершин С равнобедренных треугольников с заданным основанием AB .
4. Пусть А и В — точки плоскости. Найдите геометрическое место точек С, для которых: а) АС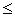 
ВС; б) АС АВ.
5. Даны три точки: А, В, С. Найдите точки, которые одинаково удалены от точек А и В и находятся на расстоянии R от точки С.
6. На данной прямой a найдите точки, удаленные от данной точки C на заданное расстояние R . Какие при этом возможны случаи?
7. Пусть А и В точки плоскости, c — прямая. Найдите геометрическое место точек прямой c , расположенных ближе к А, чем к В. В каком случае таких точек нет?
8. Пусть a и b — пересекающиеся прямые. Найдите геометрическое место точек: а) одинаково удаленных от a и b ; б) расположенных ближе к a , чем к b .
9. Пусть А, В, С — три точки, не принадлежащие одной прямой. Найдите геометрическое место точек М таких, что: а) прямая СМ пересекает отрезок АВ; б) луч СМ пересекает отрезок АВ; в) отрезок СМ пересекает отрезок АВ.
10. На прямой, пересекающей стороны угла, найдите точку, одинаково удаленную от этих сторон.
11. Дан угол АВС и точки M , N на его сторонах. Внутри угла найдите точку, одинаково удаленную от точек M и N и находящуюся на одинаковом расстоянии от сторон угла.
12. В треугольнике АВС АВ=ВС=14 см. Серединный перпендикуляр к стороне АВ пересекает сторону AB в точке D и сторону AC в точке E (рис. 5). Точка Е соединена с точкой В. Найдите сторону АС треугольника АВС, если периметр треугольника ВЕС равен 40 см.
13. В треугольнике АВС АВ=ВС=18 см. Серединный перпендикуляр к стороне АВ пересекает сторону AB в точке D и сторону ВС в точке Е (рис. 6). Точка Е соединена с точкой А. Периметр треугольника АЕС равен 27 см. Найдите сторону АС.
14. Невдалеке от двух населенных пунктов проходит шоссе. В каком месте этого шоссе нужно построить автозаправочную станцию, чтобы расстояния от нее до обоих пунктов были одинаковыми?
15. Жильцы трех домов решили совместными усилиями вырыть колодец. В каком месте следует расположить колодец, чтобы расстояния от него до домов были одинаковыми?
Источник
Отклонение точки от прямой
В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.
Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком «+», если эта точка и начало координат лежат по разные стороны прямой, и со знаком «−», если точка и начало координат лежат по одну сторону от прямой.
Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком «+», если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком «−», в противном случае.
Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 и начало координат O лежат по разные стороны прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 и начало координат O лежат по одну сторону от прямой L.
 |
На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L
 |
где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.
Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:
Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.
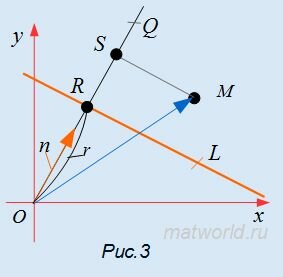
Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.
 |
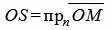 , | (3) |
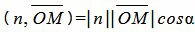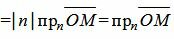  , | (4) |
где n− единичный нормальный вектор прямой L, α−угол между векторами n и 
.
Из (3) и (4) следует:
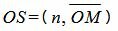 . | (5) |
С другой стороны
 , | (6) |
так как нормальный вектор прямой имеет координаты n=<cosφ, sinφ>, а точка M − M(x, y).
Сопоставляя (2), (5) и (6), получим:
Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M0(x0, y0) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M0:
Заметим, расстояние от точки M0 до прямой L будет равно модулю отклонения данной точки от прямой.
Пример 1. Задано нормальное уравнение прямой:
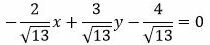 . | (7) |
Найти отклонение точки M(5,-3) от прямой (7).
Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):
  . |
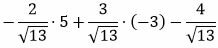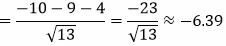Ответ. Отклонение точки M(5,−3) от прямой (7) равно:
 . |
Пример 2. Задано общее уравнение прямой:
Найти отклонение точки M(1,1) от прямой (8).
Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье «нормальное уравнение прямой»). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:
 . |
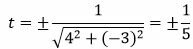Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:
 . |
Умножив уравнение (8) на нормирующий множитель, получим:
 . |
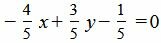Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):
 . |
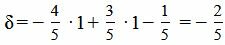Ответ. Отклонение точки M(1,1) от прямой (8) равно:
Источник
