Что значит точка решает

Точка — это. Значение и толкование слова «точка»

Точка – это короткое слово, которое имеет множество толкований. При этом оно в одних случаях обозначает объект, а в других – действие. Применяется это понятие во множестве областей. Подробно о том, что это – точка, будет рассказано в предлагаемом обзоре.

Значения в словаре

Там их дается несколько вариантов.

Одно из толкований изучаемой лексемы – «маленькое пятно». Пример: «В книгах при шифровке слева отсчитывали и отмечали букву карандашной точкой, которая была еле заметной. Она указывала на номер строчки в ключе, а с правой стороны – на порядок буквы в строчке».

Другое значение говорит о роли точки в тексте. Она представляет собой знак в различных письменностях и системах условных обозначений. Например, она может быть знаком:

• препинания, который, как правило, обозначает конец фразы;
• сокращения;
• диакритическим (над-, под-, внутристрочные знаки, используемые для уточнения и изменения других знаков);
• азбуки Морзе.

Пример: «Учительница дала задание – переписать текст, расставив в конце предложений точки. Почти всем удалось с ним справиться успешно».

Действие и процесс, соответствующие глаголу «точить». Это касается заострений лезвий путем механической обработки – вытачивания. Пример: «Для тупого ножа самая первая точка – это очень долгий процесс, но после этого действовать станет гораздо легче».

Что означает точка в математике?

Там она может изображать следующие знаки:

• умножения;
• производной;
• разделения цифр в многозначных числах;
• отделения дробной части чисел.

В евклидовой геометрии речь идет о точке как о (об):

• одном из первичных понятий, которое не подлежит определению;
• математическом объекте, задаваемом только перечнем присущих ему свойств – аксиомами;
• абстрактном объекте, не имеющем в пространстве измеримых характеристик, нульмерном объекте.

В математике говорят о таких объектах, как точка:

• возврата;
• перегиба;
• минимума;
• максимума;
• экстремума;
• бесконечно удаленная.

Пример: «Короче умножение можно обозначить следующим образом. Сначала пишется множимое, за ним ставится точка – знак умножения, а после этого – множитель».

В переносном смысле

В этом случае изучаемый объект рассматривается как характерное значение, присущее количественному параметру, при котором осуществляется качественное изменение. В такой ситуации говорится о точке:

• критической;
• росы;
• замерзания;
• плавления;
• кипения;
• испарения;
• воспламенения;
• вспышки;
• компенсационной;
• предельной;
• невозврата;
• равновесия.

Пример: «Через месяц отношения между партнерами приобрели сильный накал. Критической точкой стало то, что Олег напрочь забыл о дне рождения подруги, что и привело к разрыву».

Другие толкования

Чтобы лучше понять, что это – точка, следует рассмотреть и другие значения слова. Среди них находятся следующие:

1. У военных в разговорной речи точка – это гарнизон, позиция. Пример: «Алексей служил на точке, считавшейся отдаленной даже на этом далеком острове с очень холодным климатом. Поэтому он приобрел настоящую армейскую выучку».
2. Место, где что-то проводится, организовывается, располагается или устанавливается. Такой точкой может быть: торговая, сбора, огневая. Пример: «По результатам сдачи экзаменов в престижном университете Сергей оказался в первой тройке. Теперь он мог не волноваться о своем трудоустройстве в любой из точек Земного шара».

Сеть отелей

В Ленинградской области и в Республике Карелии появилась новая сеть гостиниц, относящихся к комфорт-классу. Это отели под общим названием «Точка на карте». В них можно найти все, что требуется для высококачественного отдыха, для восстановления сил, для того, чтобы абстрагироваться от привычного образа жизни, на несколько дней отбросить условности и окунуться в потрясающий мир северной природы.

Провести отдых в отелях, относящихся к сети «Точка на карте», – это значит воспользоваться идеальным способом знакомства с Ладожской Карелией. Этот край славится поросшими соснами скалами, кристально чистыми озерами, лесными водопадами, бархатным мхом и тишиной. Все это приятно удивляет городского жителя больше, чем любые спецэффекты. Николай Рерих называл эту землю «Терра инкогнита».

Природная красота здесь удачно сочетается с комфортными условиями, предоставляемыми сетью гостиниц. В некоторых из отелей гости могут разместиться в апартаментах модульного типа. В номерной фонд места отдыха входит 31 стандартный номер.

Каждый из них располагается в двухэтажном комплексе. Сюда включается также и номер, предназначенный для людей с ограниченными возможностями. При этом имеется девять апартаментов, относящихся к классу люкс и шесть номеров для семей. В других отелях располагается по 60 стандартных номеров и один для людей с ограниченными возможностями. Есть и другие варианты.

Движение точки

Для того чтобы описать, как движется тело, по большому счету нужно знать, как перемещаются его различные точки. Но когда происходит поступательное движение тела, то все они будут перемещаться одинаково. Поэтому, чтобы описать движение тела, являющееся поступательным, достаточно будет рассмотреть лишь движение одной из его точек.

Если же последние движутся по-разному, то в некоторых случаях ограничиваются описанием движения только одной из них. Здесь речь идет о случаях, когда интерес представляет лишь изменение положения тела как одного целого.

Например, это может иметь место, когда изучается полет пули, самолета, движение корабля в море, планет вокруг Солнца. Так, при изучении вращения планеты вокруг светила достаточно будет описания движения ее центра. Таким образом, в отдельных случаях описание движения тела аналогично описанию движения одной точки.

Различные виды движений точки различаются друг от друга в первую очередь по видам траектории. Если траектория является прямой линией, то движение будет прямолинейным, если она кривая, то движение криволинейное.

В восточной медицине

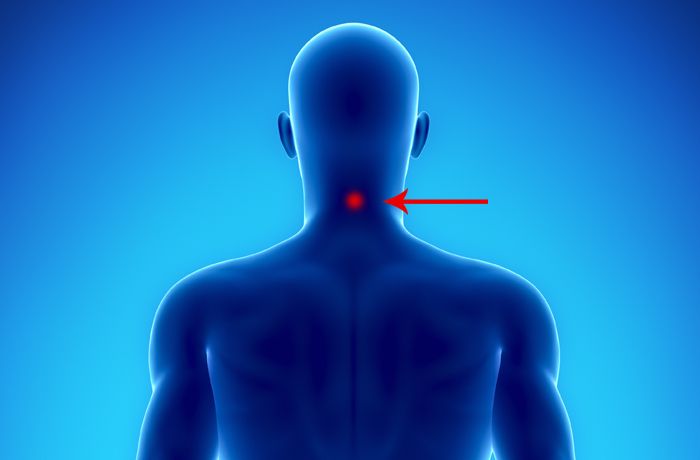
Речь пойдет о фэн-фу — точке у основания черепа. Эта зона является уникальной. При воздействии на нее удается повлиять на сам мозг, так как в этом случае между мозгом и кожей не находится больше ничего. Представители восточной медицины считают, что воздействие на нее обеспечивает максимальный эффект при лечении организма без дополнительных усилий.

Для этого к зоне фэн-фу прикладывают кусочек льда. Это место, расположенное во впадине, находящейся между шейными сухожилиями, приблизительно на три сантиметра выше того места, где начинается рост волос. Здесь шея и голова сходятся друг с другом. Здесь держать лед нужно в продолжение 20 минут. Повторяется такая процедура один раз в три дня. Для большего эффекта рекомендуется делать это на голодный желудок.

С помощью такого нехитрого метода вылечиваются органы дыхания, сердечно-сосудистая система, щитовидная железа, вегетососудистая дистония, гипер- и гопотония. Во избежание непредсказуемых последствий применять этот способ без консультации со специалистом не рекомендуется.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

На рисунке изображена прямая a и точки D, F, G и H . Точки F и G лежат на прямой a . Точки D и H не лежат на прямой a .

В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.

Задача № 1 из учебника Атанасян 7-9 класс

Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .

Решение задачи

Обозначим её буквой a .

Отметим точки (·)A и (·)B , лежащие на прямой a .

Отметим точки (·)P, (·)Q и (·)R , не лежащие на прямой a .

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

На рисунке прямые a и b не пересекаются . Прямые b и c пересекаются .

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

В тексте пересечение прямых обозначают символом ∩ . Информацию на рисунке выше можно записать следующим образом:

• b ∩ c — прямые b и с пересекаются;
• a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M . Другими словами, прямые пересекаются в точке M . Геометрическими обозначениями пересечение прямых в точке записывается так:
e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через любые две точки можно провести прямую, и притом только одну .

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M .

Третий случай расположения прямых

Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B .

Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно .

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Теперь прямая a пересекается с прямой b , прямая b пересекается с прямой c и прямая c пересекается с прямой a .

В этом случае у нас только одна точка пересечения всех прямых — точка (·)D .

Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D . Тогда получится три точки пересечения — (·)D, (·)E и (·)F .

Прямая a пересекается с прямой b в точке (·)D , прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E . Условие задачи выполнено.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T .

Сам отрезок можно назвать ST или TS . Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник