- Как пользоваться таблицей Брадиса?
- Таблица Брадиса
- Таблица синусов
- Таблица тангенсов
- Таблица косинусов
- Таблица котангенсов
- Брадис Владимир Модестович
- Тригонометрические четырехзначные таблицы Брадиса
- Зачем нужна таблица Брадиса?
- Почему таблица Брадиса — четырехзначная?
- Как пользоваться таблицей синусов?
- Что значит таблица брадиса
- Тригонометрические функции
- Часто используемые значения косинуса
- Таблица Брадиса – синусы и косинусы.
- Как пользоваться таблицей Брадиса.
- Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
- Тригонометрия. Свойства, графики тригонометрических функций.
- Прямые тригонометрические функции.
- Таблица значений тригонометрических функций sin , cos , tg для наиболее популярных углов (таблица Брадиса).
- Производные тригонометрические функции.
- Полная таблица Брадиса
- Другие тригонометрические функции.
- Тригонометрия. Обратные тригонометрические функции. Арксинус.
- Как пользоваться таблицей Брадиса косинусов или синусов
Как пользоваться
таблицей Брадиса?

Давайте на нескольких примерах посмотрим как пользоваться таблицей Брадиса.
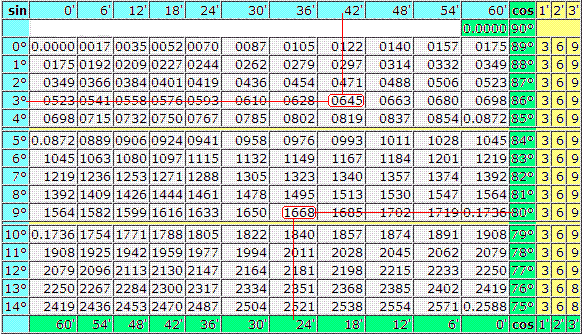
sin 7°=0.1219 косинусы смотрим снизу cos 82°=0.1392 надеюсь это понятно.
sin 3°42′=0.0645 на картинке красным цветом cos 80°24′=0.1668 то же просто
Хочу заметить все тоже самое верно и для определения значений
тангенсов и котангенсов.
Теперь возьмем более сложный вариант, если угол представленный в таблице отсутствует, то следует выбирать наиболее близкое к нему значение (из имеющегося в таблице синусов и косинусов), а на имеющуюся разницу, которая может быть 1′,2′,3′, взять поправочное значение из желтой графы, как показано в примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 или
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Так же необходимо запомнить правило, для синуса поправка имеет положительный знак, а для косинуса отрицательный
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 или
cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659
Оказывается пользоватся таблицей Брадиса не так уж и сложно. Надо еще раз очень внимательно все посмотреть, попробовать, и можно смело браться за самостоятельные расчеты.
Источник
Таблица Брадиса
Таблица Брадиса или тригонометрическая таблица, которая представляет собой сборник значений углов в градусном и радиальном измерении. Фактически является сборником таблиц, которые содержат посчитанные значения для синусов (sin), косинусов (cos), тангенсов (tg), котангенсов (ctg) и их производных. Эти значения рассчитаны до четвертого знака после запятой. Поэтому сборник и называется «Четырёхзначные математические таблицы». Ниже рассмотрим основные таблицы.
Таблица синусов
Как пользоваться таблицей синусов. Для чего она нужна таблица. Что такое синус.
Таблица тангенсов
Как вычислить тангенс угла и найти его значение с помощью таблиц Брадиса
Таблица косинусов
Самоучитель использования таблицы косинусов. Значения для углов различных градусов
Таблица котангенсов
Рассчитанные значения для котангенсов угла с точностью до 4-го знака
Брадис Владимир Модестович
Разработал «Четырехзначные математические таблицы» или «Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин» еще в 1921 году. Большое внимание уделял педагогике. Выступал за улучшение математической культуры в школах. Член-корреспондент Академии наук СССР
Самый простой и быстрый способ получить вычисленные значения для sin, cos, tg, ctg углов без использования калькулятора, компьютера и Excel. Скачать, воспользоваться и научиться пользоваться таблицей онлайн на нашем сайте можно абсолютно бесплатно!
Тригонометрические четырехзначные таблицы Брадиса
Зачем нужна таблица Брадиса?
Таблица Брадиса дает готовые рассчитанные значения синуса, косинуса, тангенса, котангенса любого угла. В отличие от калькулятора, таблицами можно пользоваться на ЕГЭ
Почему таблица Брадиса — четырехзначная?
Таблица Брадиса называется четырехзначной, потому что все рассчитанные значения получены с точностью четыре знака после запятой
Как пользоваться таблицей синусов?
Для того чтобы получить значение синуса, используя таблицы Брадиса, нужно раскрыть саму таблицу синусов и в ней, в перекрестье угла и минуты отыскать численное значение.
Источник
Что значит таблица брадиса
Советские инженеры уже ушли в прошлое. Теперь о них можно сочинять легенды. В общем, эти ребята достойны героических сказаний. Они построили крупную индустриальную страну, в которой дымили гигантские заводы, а вот ядерные реакторы, как раз, утечек не давали. По самым длинным в мире железным дорогам бежали поезда, самолёты и ракеты, во-первых, взлетали, а во-вторых, летали. И корабли воды бороздили. Что характерно, сделано это было за нищенскую зарплату и почти что вручную. В распоряжении советского инженера были нехитрые инструменты: карандаш, кульман, на нём ватман, рядом на столе – логарифмическая линейка, если повезёт, арифмометр «Феликс», а чаще всего, таблицы Брадиса.
Эти таблицы с дальнего расстояния выглядят каким-то волшебным артефактом, сэкономившим массу времени всем, кто занимался утомительными расчётами, неизбежными в любой инженерной работе. А Брадис, составивший волшебные эти таблицы, тоже выглядит волшебником, повелителем упрямых цифр.
Впрочем, волшебство здесь не при чём. Владимир Модестович Брадис (1890 – 1975) ведь был не колдуном, а был он математиком, придумавшим способ, который сократил трудоёмкость инженерных расчетов до минимума. Причём, сделал он это в начале 20-го века, задолго до того, как появились первые калькуляторы, которые, в конце концов, свели все расчётные сложности к нулю. Не говоря уже о компьютерах.
Компьютер-телефончик, маленький, но могучий, который, кажется, может всё, нынче находится у любого в кармане. Поэтому революционность изобретения Брадиса сейчас трудно объяснить. И всё же, что он сделал?
Для практических расчетов необходимо не так уж и много функций: квадраты и кубы, квадратные и кубические корни, обратная функция 1/x, а также тригонометрические функции (синусы, косинусы, тангенсы), экспонента и логарифмы. Брадис посчитал для этих функций все значения в широком интервале аргументов с определённым шагом и с приемлемой точностью. Приемлемой оказалась точность в четыре значащих цифры. Результаты расчётов были представлены в виде компактных таблиц и напечатаны, как небольшая по размеру брошюра. Название брошюры полностью отражало содержание: «Четырёхзначные математические таблицы». Эта брошюра в советское время переиздавалась едва ли не ежегодно и была очень востребована. Самое удивительное, что она до сих пор издаётся в России.Таблицы Брадиса имеют единообразную структуру для всех функций. В левом столбце и в верхней колонке каждой таблицы находятся значения аргументов находятся в левом столбце и в верхней колонке. В клетке, расположенной на пересечении столбца и колонки, находится соответствующее значение функции.
Но к чему длинные объяснения? Не лучше ли попробовать на примере? Давайте с помощью таблицы Брадиса рассчитаем значение какой-нибудь функции, например, синуса.
Откроем таблицу синусов и определим значение синуса для угла 10 градусов и 30 минут. Находим в левом столбце значение 10 градусов (11-я строка), а в верхней колонке – 30 минут (6-й столбец). На пересечении 11 строки и 6-го столбца, находим значение функции, 0.1822. Три последние столбца предназначены для уточнения значений минут. Дело в том, что в верхней колонке значения представлены только значения минут, кратные 6. Для определения синуса для других значений аргумента следует прибавить или вычесть поправку из ближайшего значения функции, представленного в таблице. Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.
Известно, что значения синуса и косинуса для определённого угла взаимосвязаны. Поэтому по таблице синусов можно определять и значения косинусов. Но аргумент для косинуса следует искать в правом столбце (четвертом справа) и в нижней строке. То же самое с тангенсом и котангенсом. Значения котангенсов ищем по таблице тангенсов аналогичным образом.
Аргументы тригонометрических функций в таблицах Брадиса заданы в градусах. Чтобы градусы перевести в радианы значение угла следует умножить на 180 и разделить на число π , приблизительное значение которого составляет 3.1415926. Кстати, таблицы радианной меры угла тоже были сосчитаны В. М. Брадисом и их можно отыскать в его знаменитой брошюре.
Итак, таблицы В. М. Брадиса позволяют определять четыре значащих цифры любой функции. Именно поэтому они называются «четырехзначными». Такой точности расчетов заведомо хватает для 90% инженерных расчетов. Кстати, когда рассчитывали траектории первых советских ракет, компьютеров ещё не было, а точности четырёхзначных таблиц было недостаточно. И пришлось таблицы Брадиса пересчитывать в восьмизначные.
Повторим ещё раз. Сейчас, когда калькуляторы встроены в мобильные телефоны, расчёты функций по таблицам Брадиса кажутся смешным пережитком прошлого. Впрочем, таким ли уж смешным, если в этом прошлом есть, чем гордиться? Большое ведь видится на расстоянии. А советские ракеты все-таки взлетали и летали.
Источник
Тригонометрические функции
Часто используемые значения косинуса
Косинус 0 градусов = 1
Косинус 30 градусов = 0,866025404 =
Косинус 45 градусов = 0,707106781 =
Косинус 60 градусов = 0,5 =
Косинус 90 градусов = 0
Косинус 120 градусов = -0,5 = <-frac <1><2>>
Косинус 135 градусов = -0,707106781 = <-frac
Косинус 180 градусов = -1
Таблица Брадиса – синусы и косинусы.
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов:


В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов :
,
и
.
Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.
Используя формулы приведения , только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.
Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса , таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число . Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.
Тригонометрия. Свойства, графики тригонометрических функций.
Прямые тригонометрические функции.
Таблица значений тригонометрических функций sin , cos , tg для наиболее популярных углов (таблица Брадиса).
α(град)
0
15
30
45
60
75
90
α(рад)
0
π/12
π/6
π/4
π/3
5π/12
π/2
α(град)
120
135
150
180
270
360
α(рад)
2π/3
3π/4
5π/6
π
3π/2
2π
Производные тригонометрические функции.
Полная таблица Брадиса
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | ± 1′ | ± 2′ | ± 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,0000 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 007 | 0087 | 0105 | 0122 | 014 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 061 | 0628 | 0645 | 0663 | 068 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 075 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0872 | 85° | 3 | 6 | 9 |
| 5° | 0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 108 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 134 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 153 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 165 | 1668 | 1685 | 1702 | 1719 | 1736 | 80° | 3 | 6 | 9 |
| 10° | 1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 184 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 213 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 225 | 77° | 3 | 6 | 9 |
| 13° | 225 | 2267 | 2284 | 23 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 247 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 2588 | 75° | 3 | 6 | 8 |
| 15° | 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 274 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 279 | 2807 | 2823 | 284 | 2857 | 2874 | 289 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 294 | 2957 | 2974 | 299 | 3007 | 3024 | 304 | 3057 | 3074 | 309 | 72° | 3 | 6 | 8 |
| 18° | 309 | 3107 | 3123 | 314 | 3156 | 3173 | 319 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 342 | 70° | 3 | 5 | 8 |
| 20° | 342 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 36 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 373 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 421 | 4226 | 65° | 3 | 5 | 8 |
| 25° | 4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 454 | 63° | 3 | 5 | 8 |
| 27° | 454 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 471 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 497 | 4985 | 5 | 60° | 3 | 5 | 8 |
| 30° | 5 | 5015 | 503 | 5045 | 506 | 5075 | 509 | 5105 | 512 | 5135 | 515 | 59° | 3 | 5 | 8 |
| 31° | 515 | 5165 | 518 | 5195 | 521 | 5225 | 524 | 5255 | 527 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 549 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 565 | 5664 | 5678 | 5693 | 5707 | 5721 | 5736 | 55° | 2 | 5 | 7 |
| 35° | 5736 | 575 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 585 | 5864 | 5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 592 | 5934 | 5948 | 5962 | 5976 | 599 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 606 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 617 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 628 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 632 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 6428 | 50° | 2 | 4 | 7 |
| 40° | 6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 66 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 673 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 682 | 47° | 2 | 4 | 6 |
| 43° | 682 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 7071 | 45° | 2 | 4 | 6 |
| 45° | 7071 | 7083 | 7096 | 7108 | 712 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 723 | 7242 | 7254 | 7266 | 7278 | 729 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 742 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 749 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 757 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 766 | 40° | 2 | 4 | 6 |
| 50° | 766 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 776 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 788 | 38° | 2 | 4 | 5 |
| 52° | 788 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 807 | 808 | 809 | 36° | 2 | 3 | 5 |
| 54° | 809 | 81 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 8192 | 35° | 2 | 3 | 5 |
| 55° | 8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 829 | 34° | 2 | 3 | 5 |
| 56° | 829 | 83 | 831 | 832 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 848 | 32° | 2 | 3 | 5 |
| 58° | 848 | 849 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 859 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 866 | 30° | 1 | 3 | 4 |
| 60° | 866 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 878 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 887 | 8878 | 8886 | 8894 | 8902 | 891 | 27° | 1 | 3 | 4 |
| 63° | 891 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 898 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 9063 | 25° | 1 | 3 | 4 |
| 65° | 9063 | 907 | 9078 | 9085 | 9092 | 91 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 915 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 933 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 95 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 965 | 9655 | 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 969 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 972 | 9724 | 9728 | 9732 | 9736 | 974 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 977 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 981 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 982 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 9848 | 10° | 1 | 1 | 2 |
| 80° | 9848 | 9851 | 9854 | 9857 | 986 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 988 | 9882 | 9885 | 9888 | 989 | 9893 | 9895 | 9898 | 99 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 991 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 993 | 9932 | 9934 | 9936 | 9938 | 994 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 996 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 998 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 999 | 999 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0° | 0 | 0 | 0 |
| 90° | 0,0000 |
Другие тригонометрические функции.
В современном мире есть 6 базовых тригонометрических функций, которые ниже в таблице указаны вместе с уравнениями, которые связывают их.
Функция
Соотношение
Тригонометрия. Обратные тригонометрические функции. Арксинус.
Как пользоваться таблицей Брадиса косинусов или синусов
Таблица Брадиса для синусов и косинусов даёт значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число минут. Так, sin 70° 30`=0.9426. Для получения синусов прочих углов нужна интерполяция, вводящая поправку на равность между данным углом и ближайшим табличным. Эта поправка берется из соответствующего столбца поправок справа (курсив). Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший меньший табличный на 1,2,3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях. Например, sin 70° 32`=0,9428, так как 9426+2=9428, и sin 70° 34`= 0,9430, так как 9432-2=9430. Та же таблица синусов и косинусов служит для разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами дополнительных углов.
Значение тангенса любого острого угла, содержащего целое число градусов и минут определяется по табл. если угол заключен между 0° и 76°, и по таблице тангенсов если между 76° и 90. Работа по таблице тангенсов и котангенсов требует применения интерполяции, облегчаемой поправками, помещенными в столбцах справа (курсив) и ничем не отличается от работы таблицы sin и cos. Тангенсы углов, которые больше 76 градусов, содержащих целое число градусов и минут, табл. дает непосредственно (без интерполяции).
Таблицы Брадиса по синусам, косинусам, тангенсам и котангенсам позволяют решать и обратный вопрос, то есть находить острый угол по данному значению его синуса или тангенса.
Источник