Что значит стягивать угол

Стягиваемый угол

3.2. Стягиваемый угол (angular subtense): Угол наблюдения a видимого размера источника при наблюдении глазом (рисунок 1) или полученный точкой измерения (см. также максимальный стягиваемый угол и минимальный стягиваемый угол), единица измерения — радиан.

Словарь-справочник терминов нормативно-технической документации . academic.ru . 2015 .

Смотреть что такое «Стягиваемый угол» в других словарях:

максимальный стягиваемый угол a_max — 3.54 максимальный стягиваемый угол amax: Значение угла стягивания видимого источника, свыше которого МДЭ и ДПИ не зависят от размера источника. Примечание amax = 100 мрад. Источник … Словарь-справочник терминов нормативно-технической документации

минимальный стягиваемый угол a_min — 3.58 минимальный стягиваемый угол amin: Значение стягиваемого угла видимым источником, свыше которого источник считается протяженным. МВЭ и ДПИ не зависят от размера источника со стягиваемым углом меньше, чем amin. Примечание amin = 1,5 мрад.… … Словарь-справочник терминов нормативно-технической документации

стягивающий угол источника a — 3.7 стягивающий угол источника a: Угол, стягиваемый видимым размером источника при наблюдении из точки пространства, как показано на рисунке 3. Примечание 1 Положение и видимый угловой размер источника зависят от положения наблюдения в пучке (см … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р МЭК/ТО 60825-9-2009: Безопасность лазерной аппаратуры. Часть 9. Компиляция максимально допустимой экспозиции некогерентного оптического излучения — Терминология ГОСТ Р МЭК/ТО 60825 9 2009: Безопасность лазерной аппаратуры. Часть 9. Компиляция максимально допустимой экспозиции некогерентного оптического излучения: 3.3 апертура, конечная апертура (aperture, aperture stop): Конечная апертура… … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р МЭК 60825-1-2009: Безопасность лазерной аппаратуры. Часть 1. Классификация оборудования, требования и руководство для потребителей — Терминология ГОСТ Р МЭК 60825 1 2009: Безопасность лазерной аппаратуры. Часть 1. Классификация оборудования, требования и руководство для потребителей оригинал документа: 3.4 административный контроль: Измерение безопасности нетехническими мерами … Словарь-справочник терминов нормативно-технической документации

большой источник — 3.19 большой источник (large source): Источник, формирующий изображение на сетчатке, такой большой, что тепловой поток в радиальном направлении (перпендикулярно оптической оси) от центра изображения к ближайшей границе биологической ткани… … Словарь-справочник терминов нормативно-технической документации

максимальная — максимальная: Максимально возможная длина ЗО, в пределах которой выполняются требования настоящего стандарта и технических условий (ТУ) на извещатели конкретных типов, Источник: ГОСТ Р 52651 2006: И … Словарь-справочник терминов нормативно-технической документации

максимальная возможная экспозиция (МВЭ) — 3.23 максимальная возможная экспозиция (МВЭ) (maximum permissible exposure (MPE)): Значение экспозиции для глаза или кожи, которое при нормальных условиях не противоречит результатам появления биологических эффектов. Значение МВЭ зависит от длины … Словарь-справочник терминов нормативно-технической документации

промежуточный источник — 3.17 промежуточный источник (intermediate source): В основном, источник, формирующий изображение на сетчатке, такой большой, что тепловой поток в радиальном направлении (перпендикулярно оптической оси) от центра изображения к ближайшей границе… … Словарь-справочник терминов нормативно-технической документации

Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия

Источник

Что значит стягивать угол

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 71. ЗАВИСИМОСТЬ МЕЖДУ ХОРДАМИ И ДУГАМИ.

Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.

При этом будем иметь в виду дуги, меньшие полуокружности.

Теорема 1. Равные дуги стя гиваются равными хордами.

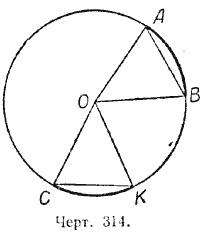
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (черт. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема 2 (обратная). Равные хорды стягивают равные дуги.

Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (черт. 314).

Доказательство. Соединим концы хорд с центром окружности— точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: АВ = СК.

Теорема 3. Большая дуга стягивается и большей хордой.

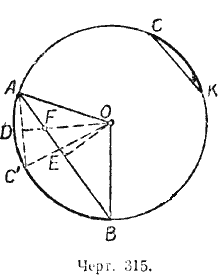
Пусть дуга АВ больше дуги СК (черт. 315).

Требуется доказать, что хорда АВ больше хорды СК.

Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С’ на дуге АВ между точками A и В, дуга СК примет положение дуги АС’, а хорда СК примет положение хорды АС’. Проведём радиусы в точки A, В и С’. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС’. В треугольнике ОFE отрезок ОЕ — катет , а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.

Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора (§ 58) катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.

Теорема 4 (обратная). Большая хорда стягивает и большую дугу.

Пусть хорда А В больше хорды СК.

Требуется доказать, что дуга АВ больше дуги СК (черт. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:

АВ СК.

Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.

Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, АВ > СК.

Источник

Окружность. Основные теоремы

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

Вписанный угол – это угол, вершина которого лежит на окружности.

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство

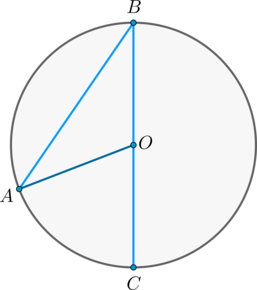
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:

Треугольник \(AOB\) – равнобедренный, \(AO = OB\) , \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\) , откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over\) .

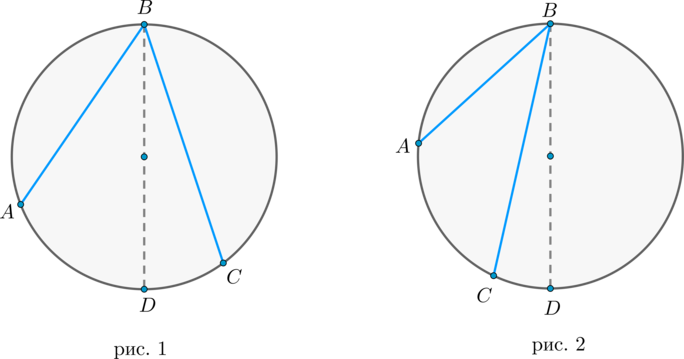
Теперь рассмотрим произвольный вписанный угол \(ABC\) . Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:

1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность, прямой.

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Определения

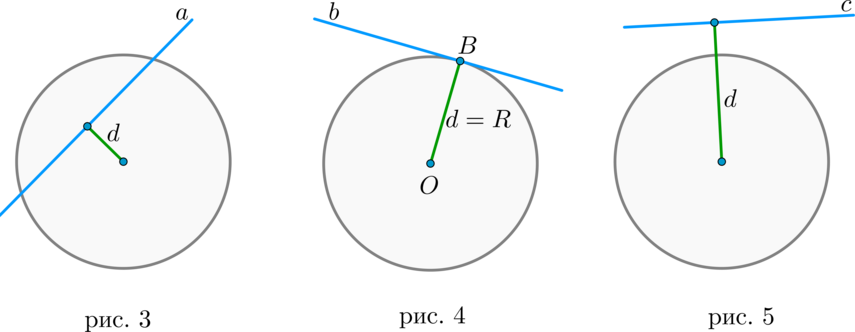
Существует три типа взаимного расположения прямой и окружности:

1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).

2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).

3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

Доказательство

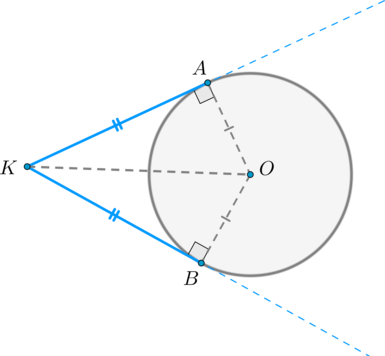
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\) :

Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\) .

Следствие

Центр окружности \(O\) лежит на биссектрисе угла \(AKB\) , образованного двумя касательными, проведенными из одной точки \(K\) .

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

Доказательство

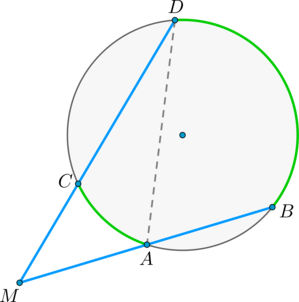
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:

Покажем, что \(\angle DMB = \dfrac<1><2>(\buildrel\smile\over — \buildrel\smile\over)\) .

\(\angle DAB\) – внешний угол треугольника \(MAD\) , тогда \(\angle DAB = \angle DMB + \angle MDA\) , откуда \(\angle DMB = \angle DAB — \angle MDA\) , но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB — \angle MDA = \frac<1><2>\buildrel\smile\over — \frac<1><2>\buildrel\smile\over = \frac<1><2>(\buildrel\smile\over — \buildrel\smile\over)\) , что и требовалось доказать.

Теорема об угле между пересекающимися хордами

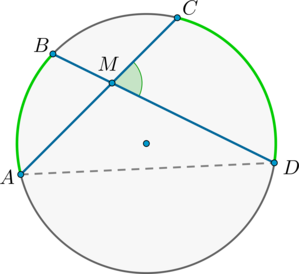
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over+\buildrel\smile\over\right)\]

Доказательство

\(\angle BMA = \angle CMD\) как вертикальные.

Из треугольника \(AMD\) : \(\angle AMD = 180^\circ — \angle BDA — \angle CAD = 180^\circ — \frac12\buildrel\smile\over — \frac12\buildrel\smile\over\) .

Но \(\angle AMD = 180^\circ — \angle CMD\) , откуда заключаем, что \[\angle CMD = \frac12\cdot\buildrel\smile\over + \frac12\cdot\buildrel\smile\over = \frac12(\buildrel\smile\over + \buildrel\smile\over).\]

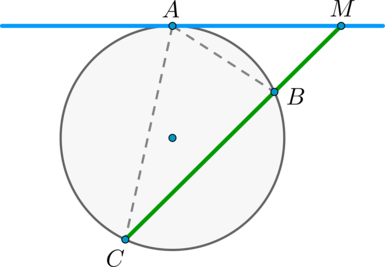
Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

Доказательство

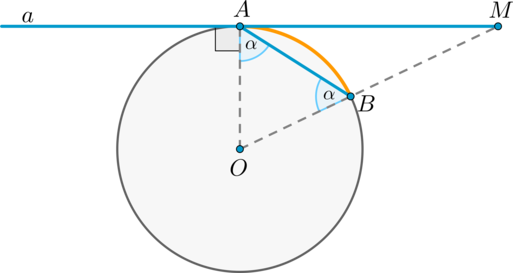
Пусть прямая \(a\) касается окружности в точке \(A\) , \(AB\) – хорда этой окружности, \(O\) – её центр. Пусть прямая, содержащая \(OB\) , пересекает \(a\) в точке \(M\) . Докажем, что \(\angle BAM = \frac12\cdot \buildrel\smile\over\) .

Обозначим \(\angle OAB = \alpha\) . Так как \(OA\) и \(OB\) – радиусы, то \(OA = OB\) и \(\angle OBA = \angle OAB = \alpha\) . Таким образом, \(\buildrel\smile\over = \angle AOB = 180^\circ — 2\alpha = 2(90^\circ — \alpha)\) .

Так как \(OA\) – радиус, проведённый в точку касания, то \(OA\perp a\) , то есть \(\angle OAM = 90^\circ\) , следовательно, \(\angle BAM = 90^\circ — \angle OAB = 90^\circ — \alpha = \frac12\cdot\buildrel\smile\over\) .

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

И наоборот: равные дуги стягиваются равными хордами.

Доказательство

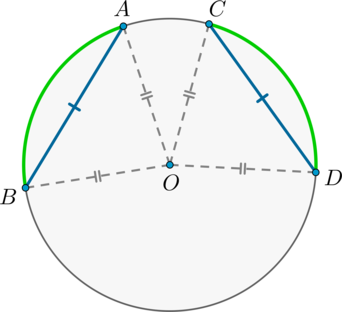
1) Пусть \(AB=CD\) . Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over=\buildrel\smile\over\) .

\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\) . Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over, \buildrel\smile\over\) соответственно, то \(\buildrel\smile\over=\buildrel\smile\over\) .

2) Если \(\buildrel\smile\over=\buildrel\smile\over\) , то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\) . Следовательно, и \(AB=CD\) .

Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

Доказательство

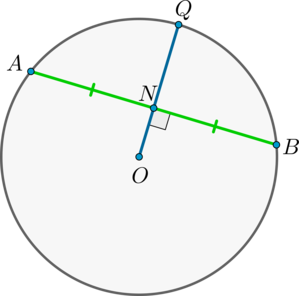
1) Пусть \(AN=NB\) . Докажем, что \(OQ\perp AB\) .

Рассмотрим \(\triangle AOB\) : он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\) .

2) Пусть \(OQ\perp AB\) . Докажем, что \(AN=NB\) .

Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\) .

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

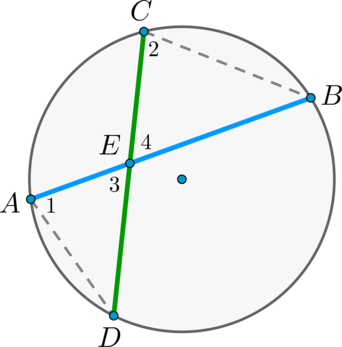
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\) .

Рассмотрим треугольники \(ADE\) и \(CBE\) . В этих треугольниках углы \(1\) и \(2\) равны, так как они вписанные и опираются на одну и ту же дугу \(BD\) , а углы \(3\) и \(4\) равны как вертикальные. Треугольники \(ADE\) и \(CBE\) подобны (по первому признаку подобия треугольников).

Тогда \(\dfrac = \dfrac\) , откуда \(AE\cdot BE = CE\cdot DE\) .

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

Доказательство

Пусть касательная проходит через точку \(M\) и касается окружности в точке \(A\) . Пусть секущая проходит через точку \(M\) и пересекает окружность в точках \(B\) и \(C\) так что \(MB . Покажем, что \(MB\cdot MC = MA^2\) .

Рассмотрим треугольники \(MBA\) и \(MCA\) : \(\angle M\) – общий, \(\angle BCA = 0,5\cdot\buildrel\smile\over\) . По теореме об угле между касательной и секущей, \(\angle BAM = 0,5\cdot\buildrel\smile\over = \angle BCA\) . Таким образом, треугольники \(MBA\) и \(MCA\) подобны по двум углам.

Из подобия треугольников \(MBA\) и \(MCA\) имеем: \(\dfrac = \dfrac\) , что равносильно \(MB\cdot MC = MA^2\) .

Следствие

Произведение секущей, проведённой из точки \(O\) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\) :

Источник