строго положительное число
Универсальный русско-английский словарь . Академик.ру . 2011 .
Смотреть что такое «строго положительное число» в других словарях:
число — сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева
Характеристическое число матрицы — Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору,… … Википедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
КОЛИЧЕСТВО — филос. категория, отображающая общее в качественно однородных вещах и явлениях. Чтобы выявить в них это общее, необходимо, во первых, установить их однородность, т.е. показать, в каком именно отношении они эквивалентны между собою, во вторых,… … Философская энциклопедия
АЛГЕБРА — раздел элементарной математики, в котором арифметические операции производятся над числами, значения которых заранее не заданы. Преимущества алгебраических методов обусловлены использованием достаточно компактных символических систем, что внешне… … Энциклопедия Кольера
Договор — (Contract) Понятие договора, виды договоров, условия договоров Информация о понятии договора, виды договоров, условия договоров Содержание > Содержание Понятие и значение . Договор и сфера его применения. Законодательное регулирование соглашения … Энциклопедия инвестора
ПРЕДИКАТОВ ИСЧИСЛЕНИЕ — общее название исчислений математической логики, являющихся формализацией тех разделов совр. логики, к рые изучают субъектно предикатную структуру предложений (высказываний), понимаемую в более широком, чем в традиц. логике, смысле: помимо теории … Философская энциклопедия
ЛИНЕЙНОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ И СИСТЕМА — дифференциальное уравнение (и система) с частными производными вида у к poro в любой точке х=( х 0, x1 . . ., х n).области его задания среди действительных переменных y0, y1 . . ., yn можно выделить (в случае надобности после надлежащего… … Математическая энциклопедия
АНАЛИТИЧЕСКОЕ МНОЖЕСТВО — подмножество полного сепарабельного метрич. пространства, являющееся непрерывным образом пространства иррациональных чисел. Понятие А. м. введено Н. Н. Лузиным [1]. Это классич. определение А. м. обобщается на случай общих метрич. и топологич.… … Математическая энциклопедия
ПОЛОЖИТЕЛЬНЫЙ — положительная, положительное; положителен, положительна, положительно. 1. Выражающий согласие, утвердительный; противоп. отрицательный в 1 знач. Положительный ответ. || Выражающий одобрение; противоп. отрицательный в 3 знач. Положительная оценка … Толковый словарь Ушакова
Источник
Что значит строгое число
Формы записи приближенных чисел
Приближенные числа записываются либо в виде конечных десятичных дробей, либо в виде целых чисел.
Определение 1 . Естественной (позиционной, с фиксированной точкой) формой записи конечной десятичной дроби называется следующая запись
. (1)
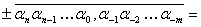
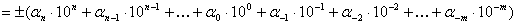
Пример 1.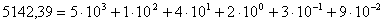 
.
Замечание 1. Определение естественной (позиционной, с фиксированной точкой) формой записи целого числа дается аналогично.
Если в левой части равенства (1) несколько первых цифр =0, то соответствующие слагаемые в правой части этого равенства писать смысла нет .
Пример 2 .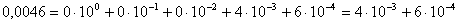 
.
В связи с этим имеет место следующее определение.
Определение 2. Значащими цифрами приближенного числа называются все цифры его записи, начиная с первой ненулевой слева.
Пример 3 . У числа 5142,39 все цифры значащие.
Пример 4. У числа 0,0046 только две значащих цифры: 4 и 6.
Пример 5. У числа 0,004600 четыре значащих цифры: 4, 6 и два последних нуля. (Для чего оставляют нули в конце числа, будет рассмотрено позднее).
Если приходится работать с большим количеством приближенных чисел, то запись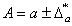 
не удобна. Поэтому решено было установить такой способ записи приближенных чисел, чтобы по самой этой записи можно было судить об их абсолютной (предельной абсолютной) погрешности.
Определение 3 . Цифра приближенного числа называется верной в широком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в широком смысле.
Пример 6. Пусть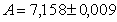 
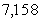
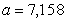
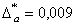
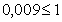
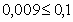
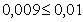
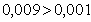
. Определим верные и сомнительные в широком смысле цифры приближенного числа 
. Заметим, что 
, 
. Т.к. 
, то цифра 7 верная в широком смысле. Т.к. 
, то цифра 1 верная в широком смысле. Т.к. 
, то цифра 5 верная в широком смысле. Т.к. 
, то цифра 8 сомнительная в широком смысле.
Определение 4. Цифра приближенного числа называется верной в узком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит половины единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в узком смысле.
Пример 7. Определим верные и сомнительные в узком смысле цифры приближенного числа 7,158 из предыдущего примера. Т.к.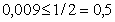 
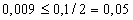
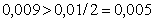
, то цифра 7 верная в узком смысле. Т.к. 
, то цифра 1 верная в узком смысле. Т.к. 
, то цифра 5 сомнительная в узком смысле. Очевидно, что цифра 8 также сомнительная в узком смысле.
Замечание 2 . Если приближенное число записывается без указания его абсолютной (предельной абсолютной) погрешности, то выписываются только верные его цифры (в узком или широком смысле). При этом верные нули в конце числа не отбрасываются. Поэтому числа 0,0344 и 0,03440 как приближенные различны: у первого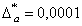 
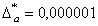
, у второго 
.
Замечание 3 . При записи целых приближенных чисел сомнительные цифры принято заменять нулями.
Пример 8 . Известно, что у приближенного числа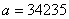 
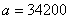
последние две цифры сомнительные в узком смысле. Поэтому правильно его записать так: 
. Нули означают, что последние две цифры – сомнительные.
В связи с рассмотренным примером возникает следующий вопрос: «Как отличить приближенное число 34200 с двумя последними сомнительными нулями от точного числа 34200?»
Определение 5 . С плавающей точкой формой записи приближенного числа называется следующая запись:
. (2)
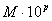
В этом случае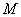 
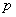
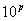
называется мантиссой числа, 
— порядком, 
— характеристикой числа.
Если число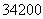 
— приближенное, то его записывают в виде (2), оставляя в мантиссе лишь верные цифры, т. е. так: 
.
Определение 6 . Если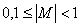 
, то запись (2) называется нормализованной формой числа.
Определение 7 . Если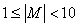 
, то запись (2) называется стандартной формой числа.
Пример 9 . В нормализованной форме число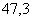 
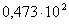
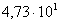
запишется так: 
, в стандартной так: 
.
Нормализованная форма используется для представления чисел в памяти компьютера (калькулятора), стандартная — для вывода чисел на экран компьютера (калькулятора), если оно не умещается на нем.
Источник
Введем обозначения
Краткая сводка теоретических сведений, необходимых для выполнения задания 1
Задание 1
Пояснения к выполнению лабораторной работы
Ход работы
Цель работы
Изучить теорию и практику оценивания погрешностей.
Исходные данные для выполнения всех заданий содержатся в таблице(числа x,a,b,c – приближенные, в из записи все цифры верны в строгом смысле, коэффициенты – точные числа)
Для выполнения заданий необходимо изучить материал гл.1 из учебника «Численные методы» подробно разобрав все приведенные в тексте примеры(лучше всего иметь под руками МК, компьютер а так же Mathcad)
Для выполнения Задания 1 требуется владение основными определениями и понятиями теории приближенных вычислений.
Для выполнения Задания 2 составляются «ручные» расчетные таблицы.
Для выполнения Задания 3 требуется владение, по крайней мере, одним из инструментальных программных средств.
Поскольку в Заданиях 2 и 3 используется одна и та же расчетная формула, в результате выполнения лабораторной работы необходимо сделать обоснованный вывод о целесообразности и эффективности использования тех или иных методов и средств вычислений.
Число х, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного числа х найдите предельную абсолютную и предельную относительную погрешности. В записи числа укажите количество верных цифр (в строгом и широком смысле).
1 Цифры числа называется верной в строгом смысле, если абсолютная погрешность этого числа не превосходит половины единицы разряда, в котором стоит эта цифра.
Округлим результат до десятых методом симметрического округления:
2 Цифра числа называется верной в широком смысле, если абсолютная погрешность этого числа не превосходит единицы разряда, в котором стоит эта цифра
3 Значащими цифрами в записи числа называются цифры в его десятичном изображении, отличные от нуля, и нули, если они расположены между значащими цифрами или стоят в конце для выражения верных знаков.
0,2409 — четыре значащие цифры;
24,09 — четыре значащие цифры;
100,700 — шесть значащих цифр;
4 Предельной абсолютной погрешностью приближенного числа хназывается – всякое число ∆х , не меньшее абсолютной погрешности еₓ этого числа.
5 Предельной относительной погрешностью ϭх приближенного числа называется отношение предельной абсолютной погрешности к абсолютному значению приближения х: ϭₓ=
δₓ-предельная относительная погрешность
еₓ-абсолютная погрешность приближенного значения
∆x-предельная абсолютная погрешность
Х— точное значение
Χ— приближенное значение
3.3 Решение:
1 В соответствии с моим вариантом (вариант 5) число Х равно
В соответствии с определением в этом числе 5 значащих цифр.
2 Округлим его до трех значащих цифр
3 Найдем предельную абсолютную погрешность для числа
∆x ≥ 0,006 – предельная абсолютная погрешность
4 Укажем количество верных цифр в строгом смысле.
По определению Цифры числа называется верной в строгом смысле, если абсолютная погрешность этого числа не превосходит половины единицы разряда, в котором стоит эта цифра
5 Абсолютная погрешность Х числа равна 0,006
6 Определим количество верных цифр в широком смысле.
По определению количество верных цифр в широком смысле Цифра числа называется верной в широком смысле, если абсолютная погрешность этого числа не превосходит единицы разряда, в котором стоит эта цифра.
Источник
