Что значит статистические факторы

С помощью этих методов анализа можно решить большинство практических задач по анализу факторных влияний на качество продукции. Все методы объединены одной целью – выяснить оказывает ли влияние некоторый фактор на качество продукции или процесса. Обратите внимание, что методы не отвечают на вопрос о том, какое влияние оказывает фактор. Чтобы оценить силу влияния фактора можно использовать как раз графический инструментарий.

Каждый метод имеет свои предпосылки использования. На основе этих предпосылок нами была разработана схема, позволяющая выбрать адекватный метод анализа в любой практической ситуации.

Схема выбора метода анализа влияния факторов

Конечно, у каждого из этих методов имеется своя не совсем простая формула расчета, но мы считаем этот вопрос вторичным, поскольку даже очень глубоко разобравшись в методологии расчета этих методов не происходит качественного скачка в понимании факторных влияний. Красота момента заключается в том, что все эти методы сегодня прекрасно реализованы в таких компьютерных программах как STATISTICA , MINITAB , SPSS , STATGRAPHICS и частично в Excel. Поэтому на долю аналитика выпадает только вопрос правильного выбора метода анализа, а также правильной интерпретации его результатов.

Выбор метода анализа определяется шкалой, в которой представлены исходные данные. Мы выделили два типа шкал – количественную и качественную. Такого разделения было достаточно для выбора графического инструмента. Однако сейчас от нас потребуются еще некоторые уточнения. Когда речь идет о количественных шкалах всегда можно поставить следующий вопрос, а подчинена ли измеряемая характеристика нормальному распределению? Чтобы ответить на этот вопрос существует много методов и подходов. Один из самых простых – построение гистограммы. На рисунке №1 показана гистограмма, которая бывает у нормально распределенных выборок. На рисунке №2 представлен случай ненормального распределения данных.

Рис. 1 Пример гистограммы, подчиненной нормальному распределению

Рис. 2 Пример гистограммы, не соответствующей нормальному распределению

(Вопросы построения гистограммы не обсуждаются в данной статье. Любое издание, посвященное статистическому управлению качества, подробно разбирает этот инструмент).

Данные представленные в качественной шкале могут иметь два и более уровней. Например, если мы анализируем влияние смены на процент несоответствующей продукции, то фактор «смена» представлен в качественной шкале. Если мы работаем в три смены, то, следовательно, этот фактор имеет ровно три уровня. Фактор «пол сотрудника», очевидно, имеет только два уровня. Если на выходе процесса качество продукции контролируется по альтернативному признаку (принять/отклонить), то мы имеем также качественную шкалу с двумя уровнями.

Предположим мы выбрали нужный метод анализа и с помощью указанного выше программного обеспечения провели необходимые вычисления. Как интерпретировать результаты? Все выделенные методы анализа в результате расчетов выводят показатель, называемый в литературе – статистическая значимость и обозначаемый латинскими буквами («р-level » или «sig.»).

Статистическая значимость — это вероятность того, что фактор не оказывает никакого влияния на качество процесса/продукта. Любая вероятность как известно может принимать любые значения от 0 до 1. Поэтому если в результате анализа мы получим запись p-level=0,76, то мы прочтем это так: «вероятность того, что фактор не оказывает влияние на качество, равна 0,76, значит, фактор не влияет.» Случаи, когда в результате анализа статистическая значимость менее 0,05 указывают о наличии влиянии фактора. Таким образом, после проведения анализа нас интересует всего один показатель – статистическая значимость.
Если статистическая значимость меньше пяти сотых, то фактор оказывает влияние на качество процесса/продукта. Степень влияния мы определяем, используя графики.

Опубликовано в журнале «Методы менеджмента качества» №12 2008 г.

Источник

Большая Энциклопедия Нефти и Газа

Статистический фактор

Статистический фактор в первую очередь определяется числом сегментов, координация перемещений которых необходима для осуществления направленного движения. [1]

Статистические факторы такого рода и определяют энтропию активации реакции. Брюс [124] нашел среднее ( экспериментальное) значение ( — ГА5 / кинетический порядок), равное 18 4 3 3 кДж — моль -, что соответствует снижению скорости в 1 7 0 3 — 103 раза на каждую дополнительную частицу, входящую в уравнение скорости и, следовательно, в переходное состояние. Дженкс [119] оценил максимальную эффективную мольность во внутримолекулярной реакции примерно в 108 моль-л — близка к наблюдаемой в случае ( 71), что соответствует проигрышу в энтропии активации в 146 Дж-К — — моль 1 в реакции с одним дополнительным участником в переходном состоянии. В случае химотрипсина ими-дазол и нуклеофильная НО-группа серина принадлежат одной и той же молекуле и фиксированы друг относительно друга сетью водородных связей системы переноса заряда. [3]

Статистический фактор связывают со статистической природой процесса усталостного разрушения. Это объясняется тем, что прочность структурных элементов материала вследствие его неоднородности изменяется случайным образом. С увеличением напрягаемых объемов детали увеличивается вероятность появления более слабых структурных элементов, что и приводит к снижению предела выносливости. [4]

Статистический фактор менее благоприятен для хелата по сравнению с комплексом с монодентат-ным лигандом, так как не все координационные места вокруг атома металла доступны для хелатообразующего лиганда. Поэтому если один конец хелатообразующего лиганда координирован металлом с определенной стороны, то для других донорных атомов лиганда доступны только те координационные места, которые находятся в ц с-положении по отношению к первому месту координации. [5]

Статистический фактор в первую очередь определяется числом сегментов, координация перемещений которых необходима для осуществления направленного движения. [6]

Статистический фактор / учитывает существование координации перемещения отдельных сегментов, соединенных первичными связями, прежде чем молекула в целом сможет двигаться под действием сдвигающей силы. Свободный объем V; представляет собой разницу между измеренным объемом и объемом, который фактически занимают молекулы полимера. Температура Т обусловливает энергию, которой обладает каждый сегмент, и число пустот в расплаве. [8]

Статистический фактор в первую очередь определяется числом сегментов, координация перемещений которых необходима для осуществления направленного движения. [9]

Статистические факторы в формуле (10.27) благоприятствуют тому, что трип летное состояние играет большую роль при рассеянии в изучаемой области энергий. [10]

Статистический фактор 1 / 3 введен здесь для учета такой ориентации, когда плоскость кольца параллельна В0 и кольцевой ток не возникает. [11]

Теперь основной статистический фактор F в уравнении (4.2) определяется числом фононов pij, которое необходимо для выполнения закона сохранения энергии. [12]

Хотя статистический фактор благоприятствует образованию циклогексилэтилена, данные об относительной устойчивости этих двух олефинов отсутствуют. [13]

Оценка статистического фактора в известной мере условна. Сравнение более ранних работ с последующими 25 74 подтверждает это. [14]

Значения статистических факторов для системы НзО — Н2О несколько неопределенны. Более правильно, как отмечено Голдом и Уотерманом [8], полагать q равным 2, поскольку в соответствии с пирамидальной структурой НзО молекула НгО обладает двумя пространственно разными, но эквивалентными местами, к которым может присоединиться протон. [15]

Источник

статистический фактор

Универсальный русско-немецкий словарь . Академик.ру . 2011 .

Смотреть что такое «статистический фактор» в других словарях:

Фактор общего интеллекта — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Фактор общего интеллекта (англ. general factor, g factor) является широко используемым, но противоречивым конструктом, используемым в психологии (см.… … Википедия

ФАКТОРНЫЙ АНАЛИЗ — Этот термин в действительности не представляет собой единого понятия, скорее он служит общим названием для ряда статистических процедур, которые направлены на определение места меньшего числа измерений, кластеров или факторов (4) в большем наборе … Толковый словарь по психологии

Нейтронная спектроскопия — нейтронная спектрометрия, область ядерной физики, охватывающая исследования зависимости эффективного поперечного сечения (См. Эффективное поперечное сечение) взаимодействия нейтронов с атомными ядрами от энергии нейтронов. … … Большая советская энциклопедия

Алканы — Эта статья о химических соединениях. О канадской алюминиевой компании см. Rio Tinto Alcan … Википедия

Метановые углеводороды — Эта статья о химических соединениях. Статью о канадской алюминиевой компании Alcan см. ациклические углеводороды линейного или разветвлённого строения, содержащие только простые связи и образующие гомологический ряд с общей формулой CnH2n+2.… … Википедия

Насыщенные углеводороды — Эта статья о химических соединениях. Статью о канадской алюминиевой компании Alcan см. ациклические углеводороды линейного или разветвлённого строения, содержащие только простые связи и образующие гомологический ряд с общей формулой CnH2n+2.… … Википедия

Парафиновые углеводороды — Эта статья о химических соединениях. Статью о канадской алюминиевой компании Alcan см. ациклические углеводороды линейного или разветвлённого строения, содержащие только простые связи и образующие гомологический ряд с общей формулой CnH2n+2.… … Википедия

Парафины — Эта статья о химических соединениях. Статью о канадской алюминиевой компании Alcan см. ациклические углеводороды линейного или разветвлённого строения, содержащие только простые связи и образующие гомологический ряд с общей формулой CnH2n+2.… … Википедия

Предельные углеводороды — Эта статья о химических соединениях. Статью о канадской алюминиевой компании Alcan см. ациклические углеводороды линейного или разветвлённого строения, содержащие только простые связи и образующие гомологический ряд с общей формулой CnH2n+2.… … Википедия

АНАЛИЗ ДИСПЕРСИОННЫЙ (ANOVA) — статистический метод, предназначенный для исследования причинной связи между переменной зависимой и одной или несколькими независимыми переменными (факторами). По числу независимых переменных, различают однофакторный А.Д., двухфакторный А.Д. и… … Социология: Энциклопедия

Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора

Источник

Статистическая значимость в экспериментах и анализе данных

Что именно имеют в виду ученые и исследователи, когда заявляют, что что-то является или не является статистически значимым? Как установить статистическую значимость и как ее интерпретировать?

Добро пожаловать в 11-ю часть серии статей о статистике в электротехнике. До сих пор мы рассматривали как высокоуровневые определения, так и конкретные примеры статистических концепций, полезных для инженера-практика. Чтобы узнать больше о том, что мы рассмотрели, ознакомьтесь со статьями, перечисленными в меню с оглавлением выше, над статьей.

Статистическая значимость: туманная концепция?

Любой, кто обычно читает исследовательские статьи, часто сталкивается со «статистической значимостью», часто сопровождаемой загадочной ссылкой на p 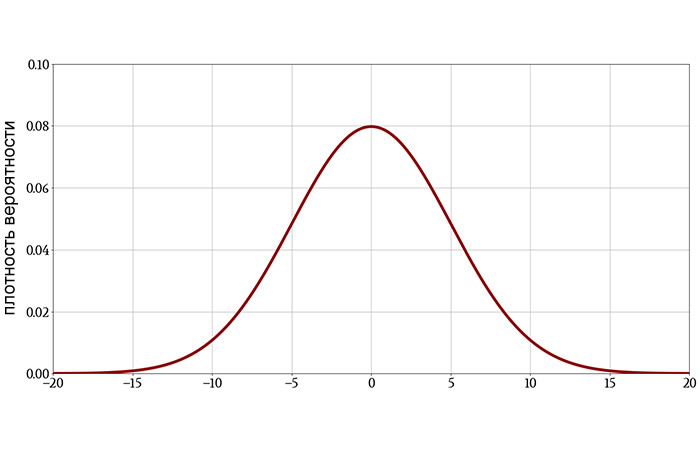Рисунок 1 – Если мы предполагаем, что нулевая гипотеза верна, мы часто будем использовать гауссову кривую в качестве функции плотности вероятности, с помощью которой мы решаем, является ли результат статистически значимым.

Порог вероятности

Статистическая значимость основана на вероятности получения результата при предположении, что нулевая гипотеза верна. Предположим, что в ходе нашего эксперимента мы получили число x (это может быть что угодно: артериальное давление, доход от продаж, средний балл теста).

Обращаясь к функции плотности вероятности, связанной с нулевой гипотезой, мы можем определить, будет ли вероятность получения x или какого-либо другого числа, которое более маловероятно, чем x, менее 5% (p 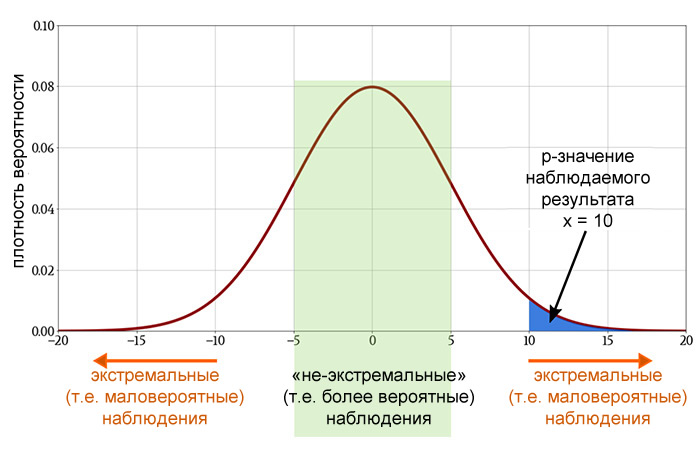Рисунок 2 – Гауссова кривая – это функция плотности вероятности, которая соответствует распределению значений, когда нулевая гипотеза верна. Мы вычисляем p-значение наблюдаемого результата путем интегрирования части этой функции плотности вероятности.

Если p-значение достаточно низкое, нет смысла продолжать предполагать, что между двумя переменными нет никакой связи. Таким образом, мы отвергаем нулевую гипотезу и утверждаем, что связь существует.

Интерпретация статистической значимости

Предыдущее объяснение описывает статистическую значимость способом, который я считаю наиболее простым и математически последовательным: если p-значение наблюдаемого результата меньше заранее определенного порога, который мы называем уровнем значимости, наблюдаемый результат очень маловероятен, если нулевая гипотеза верна. Поэтому, когда мы отвергаем нулевую гипотезу, это равносильно подтверждению того, что эксперимент обнаружил связь между интересующими переменными.

Это же общее сообщение можно передать другими способами, которые могут оказаться полезными:

• p-значение – это вероятность того, что наши наблюдения являются чистой случайностью. Таким образом, если p = 0,05, существует 5%-ная вероятность того, что результат является случайным, и 95%-ная вероятность того, что это связано с условиями, которые мы создали в нашем эксперименте.
• p-значение – это вероятность того, что мы неправильно сделаем вывод о взаимосвязи между интересующими нас переменными. Таким образом, значение p, равное 0,05, означает, что на каждые 100 экспериментов, в которых мы вывели взаимосвязь, 95 из этих взаимосвязей действительно существовали, а 5 не существовали.

Толкование слова «значимость»

Большая путаница в отношении статистической значимости возникает из-за использования слова «значимость», которое в данном контексте ограничивается конкретным статистическим использованием и не совпадает со словом «значимость» в обычном языке.

Статистически значимые результаты не обязательно являются важными или значимыми результатами. Статистическая значимость не означает практической значимости, а также отсутствие статистической значимости не означает, что экспериментальные результаты не имеют практической ценности.

Уровень значимости

Чтобы установить статистическую значимость, мы должны сравнить p-значение с уровнем значимости, обозначенным как ⍺. Уровни значимости в некоторой степени произвольны и выбираются в соответствии с условиями заданной области. Как было указано выше, часто используются ⍺ = 0,05 и ⍺ = 0,01, хотя в некоторых случаях выбирается более высокое или гораздо более низкое значение.

Заключение

Несмотря на возможное неправильное использование статистической значимости и доказательства широко распространенной неверной интерпретации, она остается важным методом в исследованиях и экспериментах. Мы продолжим изучение этой темы в следующей статье.

Источник