Что значить сравнить выражения

Сравнение выражений

Вначале рассматривается сравнение чисел с опорой на множества, и результат фиксируется с помощью знаков «больше», «меньше», «равно». После этого дети сравнивают число и выражение, найдя значение выражения, сравнивают его с данным числом.

Например, 5 ∙ 3 + 4, 5 ∙ 5 – 2. Желательно давать не только готовые выражения, но и составлять их, используя предметные действия с множествами. На третьем этапе дети сравнивают два выражения вида 10 – 5 и 3 + 4; 8 – 3 и 8 – 4. В таких выражениях сравнение можно производить не только нахождением их значений, но и наблюдением за компонентами действия. (Чем большее число мы отнимем от одного и того же числа, тем меньше будет остаток).

Работа по сравнению выражений и составлению верных равенств часто связана с преобразованием выражений на основе изучаемых свойств:

310 . 12 ∙ 310 . 10 + 310 . 2; 180 : (10 . 3) ∙ 180 : 10 . 3; (10 + 9) . 4 ∙ 10 . 4 + 9.

При сравнении выражений дети знакомятся с терминами «равенство» и «неравенство», которые могут быть верными или неверными.

В программе «Школа 2000» алгебраический материал не только связан с арифметическим материалом, но и является материалом для развития учащихся. Он намного богаче содержанием и вводится с первого класса.

Как и в традиции, составляются выражения (по рисункам), причем не только числовые, но и буквенные:

П + К а + б a + б = к, к – а = б

Рано вводятся термины «равенство», «неравенство», «выражение».

Сравнение выражений основано на рассуждении:

7 — 4 ∙ 7 + 1; а + д ∙ а – д, 8 – к ∙ 9 – к…

Правила о порядке выполнения действий рассматриваются с точки зрения алгоритмов (т.е. составление программ).

3 + (8 – 2) 3 + 8 – 2

Для закрепления правил выполняются такие упражнения

1) расставь скобки по заданной программе;

2) составь выражения по схеме-«дереву»;

3) составь программу действий в выражении

a : b – c . (d + k) . m : n

Выражение с переменной

Подготовительная работа заключается в решении задач с недостающими данными, например: Купили несколько дневников по пять рублей. Сколько заплатили за дневники?

В первом классе дети знакомятся с записями вида 12 -, где в пустой квадрат подставляются числа и вычисляются значения получившихся выражений. Здесь можно проследить зависимость разности от значения, вычитаемого и определить допустимые значения вычитаемого.

Во втором классе вместо  ставится буквы латинского алфавита, и дети учатся читать выражения вида c – d, k . 5, 28 + b и находить их значения при заданных значениях букв (переменных). Часто такие задания оформляются в виде таблицы.

Выражения с переменной очень широко используются для обобщения знаний:

1) Все законы и свойства записываются в общем виде:

(a . b ) . c = а . . (b . с) — сочетательный закон умножения,

а + b = b + а а . 0=0 . а = 0 а . 1 = а

2) Решения задач (из блиц-турниров) записываются в общем виде, с буквенными данными:

3) Вводятся условные обозначения величин и их формулы:

s = a . b ; v = a . b . c ; s = v . t

4) Производятся упрощения в выражениях: 3 + у + 10 + 5; 4 . а . 5.

Вопрос 20. Формирование представлений об уравнении. Методика обучения решению уравнений и задач, решаемых уравнением.

В начальной школе рассматриваются уравнения, содержащие только одно действие. Первоначально они решаются подбором. В дальнейшем уравнения решаются на основе зависимости между компонентами и результатами действий.

В традиционной школе уравнения вводятся во втором классе, а в других системах – с начала обучения. Дети знакомятся с терминами «уравнение» и «решение уравнения». Для закрепления этих понятий предлагаются упражнения: «Выбери среди данных записей уравнения», «Преврати (составь) уравнения». Кроме этого включаются задания такого вида:

«Угадай корни: 7 + х = 7; 7 – у = 0; n – 0 = 7; а – а = 7; b – b = 0».

Методом составления уравнения решаются некоторые простые задачи: Площадь прямоугольника 36 см 2 , длина – 9 см. Найти его ширину.

В «Школе 2000» уравнения вводятся в 3 части 1 класса. Вначале выполняются привычные операции с множествами-«мешками»:

и вводится термин «уравнение».

Опорой для решения уравнений являются понятия части и целого. В течение подготовительного периода учащиеся осваивают эти понятия в операциях с множествами и усваивают их соотношения: чтобы найти одну часть надо от целого отнять другую часть.

Последовательность введения уравнений такая же, как и в традиционной программе, но на одном уроке при закреплении могут встречаться уравнения разных видов, т.к. основа их решения похожа.

Помощниками в решении уравнениях являются:

1) рисунки весов 2 + х = 4

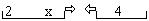
2) схемы 5 – х = 4 х + 3 = 7

3) числовые отрезки

4) уравнения с линиями

Кроме уравнений на нахождение части и целого, включены нестандартные уравнения:

26 + 26 + 26 = 26 . у ; у + у + у = 115 . 3;

145 . х = 145; 8 . х = 0 ; 5 . х = 45;

х : х = 1; х . 1 = х; 0 . х = 0; х : 0 = 0; х : 1 = х.

Во 2 классе. включены уравнения вида а . х = b, а : х = b, х : а = b

Основой для их решений является зависимость между сторонами прямоугольника и его площадью: чтобы найти сторону

х . 2 = 16

Структура уравнений во 2 кл. не меняется, только изменяется числовое множество: 200 . х = 600.

В 3 кл. происходит обобщение знаний по уравнениям: вводится термин „уравнение“, „решение уравнения“ и рекомендуется решать их с комментированием:

1. Неизвестное делимое х+3. Чтобы найти …

Уравнения содержат 3-4 действия (m . . 4+6) : 9 = 2

При изучении дробей включены уравнения

,которые решаются аналогично.

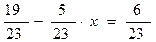
В системе РОЗ (М1А, стр. 19) вводятся термины «равенства», «неравенства», с помощью рисунков составляются верные равенства и неравенства. Неверные неравенства превращаются в верные.

Во второй четверти вводятся уравнения — дается определение уравнения, его решения (« решить уравнение – значит найти такое число, при котором получается верное равенство»). Первоначально рассматриваются уравнения вида

х + 5 = 9, которые вводятся через задачу.

Уравнения могут быть не стандартными:

( 5 + х ) + 2 = 11,где надо догадаться при сравнении равенств,

( 5 + 4 ) + 2 = 11,чему равно неизвестное.

В конце первого класса, дети знакомятся с уравнениями вида:

13 – х = 5 , 17 – а = 9, которые решаются на основе правил нахождения вычитаемого, а затем и уменьшаемого:

к – 4 = 7, к – 12 = 6.

Все виды этих уравнений даются в сравнении друг с другом:

а + 7 = 15, 15 – а = 7, а — 7 = 8,

надо выяснить связь этих уравнений и тогда найти решение.

Во втором классе продолжается работа над уравнениями, где надо найти самое большое число и воспользоваться обратными действиями:

а + 23 = 41 85 – к = 72

х . 7 = 56 е : 4 = 9

Уравнения, связанные с действиями умножения и деления решаются с помощью таблицы умножения (подбором).

Для решения уравнений другим способом изучаются основные свойства равенств:

1) а = b, ó a + c = b + c, ó a– c = b – c.

2) a = b, c 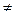0 ó a . c = b . c, ó a : c = b : c.

12х – х — 55 = 0 11х – 55 = 0

5 у + 7 = 62 5у + 7 = 62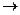

Уравнения вида 5х + 15 = 80 – 8 х , , 7 . (а – 1) = 3 . (а + 9) решаются на основе свойств равенств .

Вопрос 21. Методика изучения геометрического материала в начальной школе.

Математическое развитие школьников невозможно без приобщения их к геометрии. В начальных классах ставится задача расширить и уточнить представления учащихся о геометрических фигурах, а также развивать их пространственное мышление в процессе выполнения различных практических упражнений.

Для осуществления методической работы, направленной на решение этих задач, учителю необходимо знать, что геометрия как наука строится на базе основных понятий и аксиом, а новые факты вводятся дедуктивным путем. Школьный курс геометрии – это евклидова геометрия на плоскости и в пространстве. Эта геометрия опирается на понятие величины и ее измерения. Формирование представлений о геометрических фигурах в начальной школе связано с изучением длины и площади.

Основой формирования представлений о геометрических фигурах является способность детей воспринимать форму предмета. Эта способность позволяет узнавать, различать и изображать различные геометрические фигуры:

Основными геометрическими фигурами, изучаемыми в начальной школе, являются: точка, прямая и кривая линии, отрезок и ломаная, а затем угол, прямоугольник, квадрат, многоугольник, треугольник.

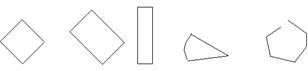Чтобы дети имели представление об этих фигурах, их достаточно показать и назвать термином (остенсивное определение). Но ученик воспринимает фигуру как целостный объект и не выделяет свойства объекта, поэтому не всегда узнает знакомые фигуры, расположенные необычно:

«не «не квадрат» «не прямоугольник» «треугольник» «многоугольник»

В дальнейшем необходимо изучать существенные свойства объектов для точных представлений о них. Для этой цели геометрические фигуры изучают в определенной последовательности, выполняя с моделями различные практические действия.

Точка— след карандаша, ручки, мела. Через точку дети проводят различные линии: прямые и кривые. Убеждаются, что через точку можно провести сколько угодно прямых и кривых, а через две точки – только одну прямую и множество кривых.

Прямая — основное и неопределяемое понятие. Если согнуть лист бумаги, то линия сгиба будет моделью прямой. Прямую через одну или две точки можно проводить только по линейке. В процессе выполнения этих упражнений дети должны научиться различать такие понятия, как: «точка пересечения двух линий», «прямая проходит через точку», или «точка принадлежит прямой» и т.д. Учащиеся могут находить прямые и кривые линии на различных геометрических фигурах: «круг», «квадрат», «прямоугольник», «пирамида», «конус», «цилиндр», «шар» и т.д.

Отрезок – это часть прямой между двумя ее точками. Отрезок имеет начало и конец, любая его точка может быть и концом и началом. Отрезок имеет длину. Отрезки можно сравнивать, складывать и отнимать, измерять.

Ученику начальных классов трудно различать такие понятия как «прямая» и «отрезок» и идти к пониманию отрезка от прямой. В просторечии слово «отрезок» почти не употребляется, говорят: «прямая», «идти по прямой», но при этом никто не имеет в виду бесконечную прямую, как принято в геометрии. Бесконечную прямую нельзя изобразить на бумаге. В учебниках математики для начальной школы принято при изображении отрезка отмечать его начало и конец точками или штрихами, чего нет в изображении прямой.

Угол можно ввести как фигуру, образованную двумя лучами, исходящими из одной точки. Такой подход к введению понятия угла возможен там, где вводится понятие луча, как части прямой, имеющей начало, но не имеющей конца. (например, М1А). В учебнике М2П углом называют часть плоскости, заключенной между двумя лучами, исходящими из одной точки, причем называют меньшую часть, т.к. плоскость делится лучами на две части.

Источник

Сравнение математических выражений

Можно научить сравнивать числовые выражения и выражения с переменной. Существуют следующие способы сравнения выражений:

• на основе нахождения значения каждого выражения и их сравнения;

• на основе знания свойств арифметических действий;

• на основе знания зависимости изменения результата действия от изменения одного из компонентов;

• на основе знания зависимости изменения результатов результата действия от изменения одного из компонентов;

• на основе знания частных случаев выполнения арифметических действий с числами 1 и 0.

Например, можно предложить найти похожие пары выражений по способу их сравнения.

6 +9 и 9 + 6; 81:9и81:3; 10 : 2 и ( 4+6 ): 2;

10*8 и 8*10; 82 – 1 и 76 + 0, 24 – 8 и 22 – 8,

22+ 7 и 22+ 14; 20*0 и 44*1; 22 + 14 и 22 + (10 + 4 );

После анализа сравнения каждой пары выражений, распределяют их на следующие группы:

1 группа 2 группа 3 группа 4 группа

6 + 9 и 9 + 6 10*8 и 8*10; 22 + 7 и 22 + 14; 20*0и44*1;

22+14 и 22+( 10+4); 81:9и81:3; 82 – 1 и 76 + 0;

10:2и(4+6):2; 24 – 8 и 22 – 8;

Сравнение выражений группы основано на знании свойств арифметических действий. Сравнение выражений 2 группы основано на нахождении значения каждого выражения и их сравнения. Сравнение выражений 3 группы основано на знание зависимости изменения результатов действия от изменения одного из компонентов. Сравнение выражений 4 группы основано на знании частных случаев выполнения арифметических действий с числами 1и 0.

На такой же теоретической основе можно провести сравнение выражений с буквенными значениями. Задание такого вида можно рассматривать как обобщение возможных способов сравнения. Например, нужно сравнить такие пары выражений:

с-8 и с — 1; в+13 и в-13;

Решение уравнений

Можно предлагать уравнения в привычном виде. Например: а+12 = 21; в-8 = 17..

Здесь можно провести игру «Принеси ответ». Урок проводится в заранее выбранном учителем месте, где ученики могут собрать разнообразный природный материал (шишки, желуди, каштаны, листья, мелкая галька и т.д.). Ученики разбиваются на несколько команд, каждая из которых получает свое задание на сбор какого-нибудь из возможных природных материалов в соответствии с решением того или иного уравнения. Собранные группы предметов сравниваются, принесшие неверное количество отдают фант или выбывают из игры. (Побочным результатом урока является появление большого количества раздаточного природного материала, который учитель использует в дальнейшей работе на уроках в классе).

Решение задач

В устном счете можно предлагать задачи простые на смекалку и на развитие логического мышления. Вычисления в этих задачах должны быть нетрудоемкими, чтобы не отнимали много времени на уроке, но заставляли думать. При этом развиваются такие приемы логического мышления и синтез, аналогия, сравнение, классификация, обобщение, необходимые для интеллектуального роста каждого ребенка. Сравнение — это сопоставление предметов и явлений с целью найти сходство и различие между ними. Анализ -это мысленное расчленение предмета или явления на образующие его части, выделение в нем отдельных частей, признаков и свойств. Синтез — это мысленное соединение отдельных элементов, частей и признаков в единое целое. Анализ и синтез неразрывно связаны, находятся в единстве друг с другом в процессе познания. Анализ и синтез — важнейшие мыслительные операции.

Абстракция — это мысленное выделение существенных свойств и признаков предметов или явлений при одновременном отвлечении от несущественных. Абстракция лежит в основе обобщения. Обобщение -мысленное объединение предметов и явлений в группы по тем общим и существенным признакам, которые выделяются в процессе абстрагирования. Процессам абстрагирования и обобщения противоположен процесс конкретизации. Конкретизация — мыслительный переход от общего к единичному, которое соответствует этому общему. В учебной деятельности конкретизировать — значит привести пример.

В процессе обучения в школе совершенствуется и способность школьников формулировать суждения и производить умозаключения. Суждения школьников развиваются от простых форм к сложным постепенно, по мере овладения знаниями. Первоклассник в большинстве случаен судит о том или ином факте односторонне, опираясь на единичный внешний признак или свой ограниченный опыт. Его суждения, как правило, выражаются в категорической утвердительной форме. Высказывать предположения, выражать и, тем более, оценивать вероятность, возможность наличия того или иного признака, той или иной причины ребенок еще не может.

Умение рассуждать, обосновывать и доказывать то или иное положение более или менее уверенно и правильно тоже приходит постепенно и в результате специальной организации учебной деятельности.

Развитие мышления, совершенствование умственных операций, способности рассуждать прямым образом зависят от методов обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам — необходимое условие успешного усвоения учебного материала. Широкие возможности в этом плане дает решение задач разными способами, получение из них новых, более сложных задач и их решение в сравнении с решением исходной задачи.

В учебнике имеются задачи, требующие найти сумму нескольких значений одной величины, в которых каждое последующее значение больше или меньше предыдущих значений на несколько единиц. Составление сокращенной записи условия таких задач с их анализом, при котором записываются не только числа, но и выражения, не только укорачивает условие задачи, но и делает более прозрачный путь к ее решению.[13]

Решая задачи, которые включают в себя простые задачи, сокращенная запись условия задачи, при которой записываются выражения, учащиеся не только воспроизводят знания связей между числовыми значениями простых задач, но и обогащаются знаниями о новых связях, на основе которых сочетаются простые задачи.

1. В курс математики начальных классов включены составные задачи, которые имеют несколько числовых значений различных величин и связанных различными зависимостями. В решении таких задач многие учащиеся затрудняются.

Сокращенная запись условия задачи, при которой “прозрачные” связи зависимости между числовыми значениями величин записываются с помощью математических выражений, значительно облегчает разбор и решение задачи. При этом задача разделяется на две части: на “прозрачную” часть и часть, в которой зависимость между числовыми значениями величин дана в завуалированном виде.

При решении многих задач учащиеся допускают ошибки из-за того, что не умеют представить жизненную ситуацию, описанную в задаче, и не умеют осознать отношения между величинами.

Ко всем ли задачам нужна краткая запись? Конечно, нет. В учебниках имеются задачи с небольшими числами, кратко сформулированные, решение которых дети могут легко записать с помощью математического выражения.

Решить задачу[14] — объяснить какие действия нужно выполнить над данными в ней числами, чтобы после вычисления получить число, которое нужно узнать. Решение задачи — упражнение, развивающее мышление. Мало того, решение задач способствует воспитанию терпения, настойчивости, пробуждению интереса к процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.

Решение задачи надо начинать с глубокого и всестороннего анализа задачи. Первое, что нужно — расчленить формулировку задачи на условия и требования. Анализ задачи должен быть всегда направлен на ее требования. Результаты анализа фиксируются схематической записью задачи. Часто удобнее использовать разного рода графические схемы, чертежи. Весь этот анализ составляет первый этап процесса решения задачи. Второй этап — схематическая запись задачи. Третий этап — поиск плана решения задачи. Четвертый этап -осуществление решения задачи. Пятый этап — проверка решения задачи. Шестой этап — исследования задачи. Седьмой этап — формулирование ответа. Восьмой этап — анализ решения задачи (установить, нет ли другого более рационального решения задачи и др.) Умение решать задачу, проникать в ее сущность — это главное в умении решения задачи.

В программе для начальной школы сказано о том, что дети должны учиться решать задачи разными способами Что же значит “решить задачу разными способами”?

Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решения или последовательностью этих связей.[15]

В методике выделяют следующие способы решения:

Рассмотрим задачу: “10 открыток разложили по 2 в несколько почтовых ящиков. Во сколько ящиков разложили открытки ?”

1. Арифметический способ

Ученики рассуждают: “Всего 10 открыток. В каждый почтовый ящик положили по 2 открытки. Нужно узнать сколько раз по 2 содержится в 10. Для этого надо 10 : 2 = 5 ( ящ.)”

2. Алгебраический способ

“Обозначим за X число ящиков. В каждом ящике было по 2 открытки.

Тогда (2 X) — все открытки. В задаче сказано, что всего 10 открыток. Записываем и решаем уравнение:

3. Графический способ.

Целесообразно различать либо различные арифметические способы решения задачи, либо различные алгебраические способы. Форма записи различных способов решения задач может быть либо по действиям, либо выражением. Осознание реальной ситуации и использование ее для поиска различных способов решения имеет большое практическое значение. Различные подходы к анализу задачи приводят к разным способам ее решения.

При решении задач разными способами необходимо использовать прием сравнения решений задач. Этот прием позволяет ответить на вопросы: какой способ решения рациональнее, в чем преимущество одного способа перед другим. Каждый новый способ решения позволяет взглянуть на задачу по иному, глубже понять связи и отношения между данным и искомым.

Применение различных способов решения задач в учебном процессе прививает интерес к математике, способствует развитию математического мышления.

Более подробно остановимся на графическом способе решения задач. Чертеж хорошо помогает ребенку осмыслить содержание задачи и зависимость между величинами. Рисование графической схемы заставляет ученика внимательно читать текст задачи, дает возможность искать различные способы решения, позволяет перенести часть умственных действий в действия практические.

В каждом виде изучения вычислений можно использовать игровые формы. Например, такие игры:

Предлагаемые уроки-путешествия, уроки-экскурсии, уроки- игры в основном будут способствовать закреплению и расширению знаний и представлений, полученных на уроках, проходящих в классе с использованием заданий учебника. Исключение составляет материал, связанный с объектами трехмерного пространства, который входит в программу первого класса, но, в силу своей специфики, не отражен на страницах учебника.

1. Урок-путешествие по теме «Наши встречи с математикой». Урок желательно провести в окрестностях школы, проложив маршрут так, чтобы можно было посетить несколько разных магазинов, пройти мимо домов разной высоты, перейти или хотя бы посмотреть на улицы разной ширины. Во время путешествия дети измеряют отдельные, выбранные учителем, отрезки пути шагами, считают повороты налево и направо. Желательно, чтобы учитель при участии детей составил план пройденного пути. (Учебник часть 1, с. 4-7).

Целью данного урока является ознакомление с понятием натурального числа, и формирование абстрактного мышления – предметы в мире отличаются, но их количество можно выразить через те же самые числа.

Задачи урока: 1) заинтересовать детей математикой; 2) дать понятие натурального числа; 3) дать навыки счета и сравнения чисел между собой.

2. Урок-игра по теме «Ориентация в пространстве». Урок проводится на свежем воздухе или в помещении, которое позволит назвать большое количество предметов в любом названном учителем направлении — слева, справа, сзади, спереди, вверху, внизу, перед, за. Класс разбивается на 2 команды, которые попеременно называют предметы, расположенные в заданном направлении. Команда, которая не смогла назвать предмет, отдает фант. В конце игры фанты разыгрываются. В процессе игры желательно несколько раз менять местоположение команд, что позволит рассмотреть положение предметов с разных позиций. (Учебник, часть 1, с. 6-8, 11-14).

Целью данного урока является ознакомление с основными координатами пространства.

Задачи урока: 1) развить навыки коллективной работы; 2) дать понятие направления в пространстве; 3) сформировать практические навыки определения направления в пространстве.

3. Урок-экскурсия «Геометрия вокруг нас». Урок можно провести, следуя потому же маршруту, который был использован на уроке 1, но теперь основное внимание сосредотачивается на форме окружающих предметов, среди которых дети стараются найти похожие, а также на поиске в объемных предметах знакомых плоскостных фигур (кругов, многоугольников разной формы и т.д.). (программный материал, не отраженный в учебнике).

Целью данного урока является ознакомление с понятием формы, и формирование абстрактного мышления – предметы в мире отличаются, но их форму можно свести к определенному набору фигур.

Задачи урока: 1) заинтересовать детей геометрией; 2) дать понятие формы предмета; 3) дать навыки определения форм и сравнения их между собой.

4. Урок-путешествие на тему «Зачем людям нужны числа». Урок проводится в окрестностях школы по маршруту, на котором ученики могут увидеть различные объекты, в которых использованы числа (номера домов, маршрутов автобусов и других видов транспорта, шкалы весов, цены товара и т.д.). При проведении урока желательно использовать стихотворение[16]

Все числа потерялись,

Исчезли без следа.

Как дом или квартиру

Без номера найти?

И к другу в день рожденья

Ведь стрелка не покажет Нам время на часах, И сколько весят фрукты, Не видно на весах. Отныне заблудиться. Не стоит и труда: Автобус без маршрута Уходит в никуда.

5. Урок-экскурсия на тему «Линии вокруг нас». Урок желательно провести там же, где проходил урок 3, но сосредоточив внимание на поиске линий, как части рассматривавшихся на нем объемных и плоскостных объектов. (Учебник часть 1,с. 19,23,27,29,36,41,43)[17].

Целью данного урока является ознакомление с понятием линии, и формирование абстрактного мышления – предметы в мире отличаются, но их форму можно свести к определенному набору линий.

Задачи урока: 1) заинтересовать детей геометрией; 2) дать понятие линии; 3) дать навыки определения линий и их направлений.

6. Урок-игра «Движемся по плану» (завершение работы над ориентацией в пространстве с использованием одного направления). На пришкольном участке или в любом выбранном для проведения урока помещения заранее устраиваются «тайники» с сюрпризами по числу команд, на которые учитель разделит учеников. Для каждой команды заготавливается план движения к одному из тайников с указанием поворотов и длины проходок по прямой между ними в шагах или с использованием любой другой мерки, которая вручается команде (это может быть палочка, кусок шнура и т.д.). Желательно, чтобы на каждом отрезке пути число мерок не превышало 9. Игра завершается, когда все команды найдут свой тайник. Те, кто справился с заданием раньше, могут по просьбе отставших оказывать им помощь. (Команды должны быть примерно равными по возможностям). (Учебник, часть 1, с. 29, 47, 60, 63).

Целью данного урока является закрепление понятия направления, и формирование абстрактного мышления – все многообразие перемещений можно свести к определенному набору направлений.

Задачи урока: 1) заинтересовать детей геометрией; 2) закрепить представление об основных направлениях в пространстве; 3) дать навыки определения направлений и движения по плану в пространстве.

Заключение

В результате проведенного исследования согласно поставленным задачам было подтверждено, что в педагогической работе большое внимание следует уделять дидактической игре на уроке. Дидактическая игра содействует лучшему пониманию математической сущности вопроса, уточнению и формированию математических знаний учащихся. Игры можно использовать на разных этапах усвоения знаний: на этапах объяснения нового материала, его закрепления, повторения, контроля. Игра позволяет включить в активную познавательную деятельность большее число учащихся. Она должна в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Отсюда можно сделать вывод о том, что использование игры необходимо при обучении детей младшего школьно возраста.

Также в ходе исследования была рассмотрена методика изучения арифметических действий, разграничены понятия вычислительного приема и вычислительного навыка. В ходе исследования была рассмотрена классификация вычислительных приемов

В результате были изучены этапы формирования вычислительных навыков в начальной школе и альтернативные подходы в изучении этих приемов, а так же сложности связанные с использованием этих альтернативных подходов.

1. Бантова М. А. Методика преподавания математики в начальной школе. Москва “Просвещение” 1984.

2. Бантова М.А. Решение текстовых арифметических задач.// “Начальная школа” №10-11 1989г. МОСКВА. «Просвещение».

3. Гребенникова Н.А. Ознакомление первоклассников с задачей. // “Начальная школа” №10 1990г. МОСКВА. «Просвещение».

4. Зеньковский В.В. Психология детства. – М., 1996.

5. Коваленко В.Г. Дидактические игры на уроках математики. М., 1990

6. Коннова В. А. “Задания творческого характера на уроках математики”.// Начальная школа 1995 №12 стр. 55.

7. Крупская Н.К. О дошкольном воспитании. М. 1973г.

8. Кудрявцев В.Т. Развитое детство и развивающееся образование: Культурно-исторический подход. – Ч.1. – Дубна, 1997. – с.85.

9. Кутьина Е. В. Влияние решения задач разными способами на развитие логического мышления учащихся начальной школы.

10. Лэндрет Г.Л. Игровая терапия: Искусство отношений. – М., 1994. – С.47.

11. Макаренко А.С. Соч.М. 1957г.

Моро М. И. “Математика в 1 — 3 классах” Издательство Москва “Просвещение” 1971.

12. Маш. Л. Граник Г. «Моя самая первая книжка по математике» М., Издательский дом «Дрофа», 1995. (Учебник часть 1, с 20-21)

13. Подластый И.П. Педагогика начальной школы – М. 2001 – с.199

14. Психолого-педагогические особенности проведения дидактических игр. Под.ред. Акшиной А., Акшиной Т., Жарковой Т. М., 1990

15. Селиванов В.А. Основы общей педагогики: Теория и методика воспитания: Учеб. пособие для студ. Высш. Пед. Учеб. заведений / Под ред. В.П.Сластенина. – 2-е изд., испр. – М.: Издательский центр “Академия’,2002.

16. Ситаров В.А. Дидактика М. 2002

17. Сластенин В.А. и др. Педагогика: Учеб. пособие для студ. Высш. Пед. Учеб. заведений/ Под ред. В.П. Сластенина. – М.: Издательский центр “Академия”, 2002.

18. Чилинрова Л., Спиридонова Б. Играя, учимся математике. М., 1993

19. Шарапова М. Ю. “Работаем по-новому”// Начальная школа 1995 №7 стр. 29.

20. Шпунтов А.И. Роль учебно-познавательных и воспитательных задач на уроках обучения грамоте// Начальная школа. – 1993.

21. Шульга Р.П. Решение текстовых задач разными способами – средство повышения интереса к математике. //“Начальная школа” №12 1990г. МОСКВА. «Просвещение».

[1] Педагогика под ред. Сластенина В.А. М. – 2002 – с. 88.

[2] Шпунтов А.И. Роль учебно-познавательных и воспитательных задач на уроках обучения грамоте// Начальная школа. – 1993.

[3] Селиванов В.А. Основы общей педагогики: Теория и методика воспитания: Учеб. пособие для студ. Высш. Пед. Учеб. заведений / Под ред. В.П.Сластенина. – 2-е изд., испр. – М.: Издательский центр “Академия’,2002.

[4] Шпунтов А.И. Роль учебно-познавательных и воспитательных задач на уроках обучения грамоте// Начальная школа. – 1993.

[5] Лэндрет Г.Л. Игровая терапия: Искусство отношений. – М., 1994. – С.47.

[6] Шпунтов А.И. Роль учебно-познавательных и воспитательных задач на уроках обучения грамоте// Начальная школа. – 1993. С. 325

[7] Шпунтов А.И. Роль учебно-познавательных и воспитательных задач на уроках обучения грамоте// Начальная школа. – 1993. С. 267

[8] Бантова М. А. Методика преподавания математики в начальной школе. Москва “Просвещение” 1984. С. 78

[9] Коннова В. А. “Задания творческого характера на уроках математики”.// Начальная школа 1995 №12 стр. 55.

[10] принцип наглядности; Моро М. И. “Математика в 1 — 3 классах” Издательство Москва “Просвещение” 1971. С. 112-114

[11] Ситаров В.А. Дидактика М. 2002 – с. 134.

[12] Подластый И.П. Педагогика начальной школы – М. 2001 – с.199

[13] Шарапова М. Ю. “Работаем по-новому”// Начальная школа 1995 №7 стр. 29.

[14] Кутьина Е. В. Влияние решения задач разными способами на развитие логического мышления учащихся начальной школы. С. 56-57

[15] Бантова М.А. Решение текстовых арифметических задач.// “Начальная школа” №10-11 1989г. МОСКВА. «Просвещение».

[16] Л.Маш, Г.Граник «Моя самая первая книжка по математике» М., Издательский дом «Дрофа», 1995. (Учебник часть 1, с 20-21

[17] Шульга Р.П. Решение текстовых задач разными способами – средство повышения интереса к математике. //“Начальная школа” №12 1990г. МОСКВА

Источник