Что значит спектр частот

Спектр частот

29. Спектр частот

Совокупность частот гармонических составляющих колебаний, расположенных в порядке возрастания

47. Спектр частот

Совокупность частот гармонических составляющих колебаний, расположенных в порядке возрастания

Словарь-справочник терминов нормативно-технической документации . academic.ru . 2015 .

Полезное

Смотреть что такое «Спектр частот» в других словарях:

спектр частот — периодических колебаний; спектр частот Совокупность частот гармоник периодических колебаний … Политехнический терминологический толковый словарь

спектр частот — dažnių spektras statusas T sritis fizika atitikmenys: angl. frequency spectrum vok. Frequenzspektrum, n rus. спектр частот, m; частотный спектр, m pranc. spectre de fréquences, m … Fizikos terminų žodynas

спектр частот периодических колебаний — спектр частот периодических колебаний; спектр частот Совокупность частот гармоник периодических колебаний … Политехнический терминологический толковый словарь

спектр — 01.02.14 спектр (сигнал или шум) [spectrum ]: Совокупность синусоидальных колебаний, представляющая в полосе частот изменяющийся во времени сигнал или шум, причем каждое колебание характеризуется собственной частотой,… … Словарь-справочник терминов нормативно-технической документации

Спектр — У этого термина существуют и другие значения, см. Спектр (значения). Спектр (лат. spectrum «видение») в физике распределение значений физической величины (обычно энергии, частоты или массы). Графическое представление такого… … Википедия

Спектр (значения) — Спектр: Содержание 1 Математика и физика 2 Космические исследования 3 Товары и изделия … Википедия

СПЕКТР — (1) совокупность семи цветовых полос (спектральные цвета), чередующихся в определённом порядке, которые получаются при прохождении светового луча через преломляющую среду (напр. радуга, образующаяся вследствие преломления солнечных лучей в каплях … Большая политехническая энциклопедия

Спектр излучаемого радиосигнала — спектр сигнала, имеющего вид нормально модулированной несущей, излучаемой пакетами во временных окнах кадра TDMA. Спектр оценивается как уровень мощности, измеренный на разном расстоянии от несущей в заданной полосе частот и в заданных интервалах … Официальная терминология

Спектр колебаний (вибрации) — – совокупность соответствующих гармоническим составляющим значений величины, характеризующей колебания (вибрацию), в которой указанные значения располагаются в порядке возрастания частот гармонических составляющих. Примечания. Периодическим … Энциклопедия терминов, определений и пояснений строительных материалов

СПЕКТР ЗВУКОВОЙ — (англ. sound spectrum) объективная характеристика звука сложного состава, отображающая его «внутреннюю» физическую структуру (в отличие от «внешней» структуры, отображаемой формой колебаний или осциллограммой). С. з. графически представляет… … Большая психологическая энциклопедия

Источник

Спектр частот света или спектр волн света?

Прежде чем читать и разбираться с этой статьёй, необходимо ознакомиться со статьёй ”Что такое волна?“.
http://samlib.ru/n/nikolaew_s_a/chtotakoewolna.shtml
Эта статья Ссылки находятся внизу в разделе РЕЦЕНЗИИ

А теперь давайте разбираться, что такое частотный спектр света и как в данном вопросе нас специально дурачат? В астрономии от светящегося объекта наблюдатель принимает спектр частот. Вот пример. Солнечный луч света – это множество цветных линий, которые мы наблюдаем как радугу. Каждая тоненькая линия – это монохроматическая частота (одна частота). Каждую монохроматическую частоту приносят частицы фотоны, обладающие этой одной частотой. Вы заметили, что наблюдать можно только линии частот (радуга), а наблюдать длину волны невозможно потому, что её у фотонов просто нет. Фотоны – это частицы, а у частиц волн нет. Частицы могут только совершать колебания. А это не одно и тоже. У фотонов нет также и характеристики длина волны. У фотонов речь может идти только о частотах или спектрах частот.
Необходимо понимать, что эффект зрения основан на частотах, которые переносятся частицами фотонами и которые колеблются, а не волнуются.
Но везде, где речь заходит о частотах света или спектрах частот, то обязательно сразу в качестве единиц измерения применяют единицы длины волны.
Например. Для человека видимый спектр: от 380нм — фиолетовый цвет до 760нм — красный цвет. Вне этого диапазона наше зрение не видит. Но задумайтесь, ведь глаза видят частоты в виде монохроматических частот, либо смеси частот в виде спектра. А никаких длин волн глаза не видят.
Вот ещё пример. Везде, где графики со спектрами частот, размерность должна быть в Гц. Однако Вас везде обманывают и специально вместо частот всегда пишут размерность длины волны, которой на самом деле у фотонов нет. Например, график солнечного спектра частот, а по оси абсцисс пишут размерность длин волн. Кроме того, одна из главных характеристик солнечного спектра специально называется максимальная длина волны (л) излучения (формула Вина л = b/T) вместо максимальной частоты излучения.
ПРИМЕЧАНИЕ. Назовите прибор, который измеряет длину волны? Таких приборов нет, даже для акустических измерений. В акустике и электромеханике измеряется только частота. Затем все обязаны по акустической формуле V=лv рассчитать длину волны и для акустики и для электромеханики, где V — скорость звука, а л — длина волны. Применение формулы С=лv для излучения, где C — скорость света. Это обман и просто невежественно. Сжимается только акустическая волна V=лv. Фотон – это частица с поперечными колебаниями, и сжать фотон невозможно.
Фотон – частица света. Характеристиками фотонов являются: масса, частота, амплитуда и инерция (энергия).
На рисунке изображена спектральная кривая солнечного излучения. Рисунок взят из справочника. Во всех остальных справочниках и учебниках то же самое. Вы нигде не найдёте рисунок спектра с единицами измерения частоты в Гц, везде по оси абсцисс будут единицы измерения в единицах длины.

Этот обман нужен для того, чтобы подтверждались математические теории Эйнштейна, в которых свет (фотоны) является волной. И, чтобы Вы не забывали, везде Вас обманывают. Где только можно. Везде, где излучение упоминание о частотах будет исключено. Например, микроволновка и так далее.
ПРИМЕЧАНИЕ. На всех графиках, где изображаются частотные спектры, в данном случае, частотный спектр Солнца, по оси абсцисс пишут вместо частот размерность длины волны, которой на самом деле у фотонов нет. Это делается всегда и везде (с 1905 года, года вы-хода в свет СТО Эйнштейна) и специально, чтобы этим подтверждались математические теории Эйнштейна, в которых свет (фотоны) является волной. А свет не волна и пересчитывать всегда частоту в длину волны по акустической формуле С=лv просто обман. Спектр частотный, а не волновой. Спектр частот, но не волн.
Посмотрите на частоты видимого света от 750 ТГц (380нм) до 385 ТГц (760нм). Некоторые видят их впервые потому, что негласно их писать запрещено. Зато в единицах длины все помнят. Как это делается. В утверждённой программе образования можно писать только длины волн и это обязательно для всех. Подумайте, нужна Вам такая утверждённая про-грамма образования?
Не разрешайте себя зомбировать утверждённой программой образования, думайте о том, что Вас заставляют заучивать. Там очень много ошибочного, специально для Вас под-сунутого.
Об ошибках в физике здесь более 100 статей
http://samlib.ru/n/nikolaew_s_a/

Документы по борьбе с инакомыслием в науке.
1. Постановление ЦК ВКП(б) от 25.01.1931г.
Запрещение рассмотрения проблем физических взаимодействий на механической, ма-териалистической основе.
2. Специальное постановление ЦК ВКП(б) от 1934г.
О дискуссии о релятивизме.
Жертвами этого постановления стали Н.А.Козырев и Н.П.Бронштейн.
3. Постановление ЦК ВКП(б) от 05.12.1942г.
4. Постановление Президиума АН от 1964г.
В этом постановлении предписывалось объявлять параноиками всех, кто критикует теории относительности Эйнштейна.
Сразу было выявлено 24 параноика среди учёных.
5. Постановление Президиума РАН от 1998г.
О создании комиссии по борьбе с лженаукой и фальсификации научных исследований во главе с академиком Э.П.Кругляковым.
Комиссия исправно функционирует.
Комиссия не скрывает, что следует принципу: ”Всё, что противоречит теориям Эйнштейна и теории ”Большого Взрыва“, является лженаукой“.
Главные идеологи этого мракобесия С.И.Вавилов, А.Ф.Иоффе, В.Л.Гинзбург.

ДОПОЛНЕНИЕ. Кроме того, частоту собственных колебаний фотонов невозможно экспериментально измерить ни в одном диапазоне.
Во-первых, нет эффектов, позволяющих измерить собственную частоту фотонов (света).
Во-вторых, нет таких частотомеров, которые могли бы измерить, например, собственную частоту фотонов видимого света, которая равна 10 в 15 степени Гц.
Есть только прибор пирометр, который определяет электрическим способом цвет, а да-лее по цвету и выдуманной фальшивой формуле Вина, пожалуйста, Вам и частота.
Все частоты в шкале электромагнитных излучений фальшивые. Например, в радиодиапазоне вместо собственной частоты радиофотонов подсунута частота следования фотонов. Однако это не одно и то же.
Это очень ёмкий вопрос и он изложен в книге С.А.Николаева «Ложь об электромагнит-ной волне и шкале электромагнитных излучений», СПб, 2014г.
А также в 8 издании книги С.А.Николаева «Эволюционный круговорот материи во Вселенной», СПб, 2015г.

Источник

Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.

При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.

Гармонические и негармонические сигналы.

И для начала давайте чуть подробнее разберемся, как же классифицируются сигналы. В первую очередь нас интересуют гармонические сигналы. Их форма повторяется через определенный интервал времени T , называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса — гармонические и негармонические. Гармонический сигнал — это сигнал, который можно описать следующей функцией:

Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Вы спросите — а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac<\pi><2>\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂

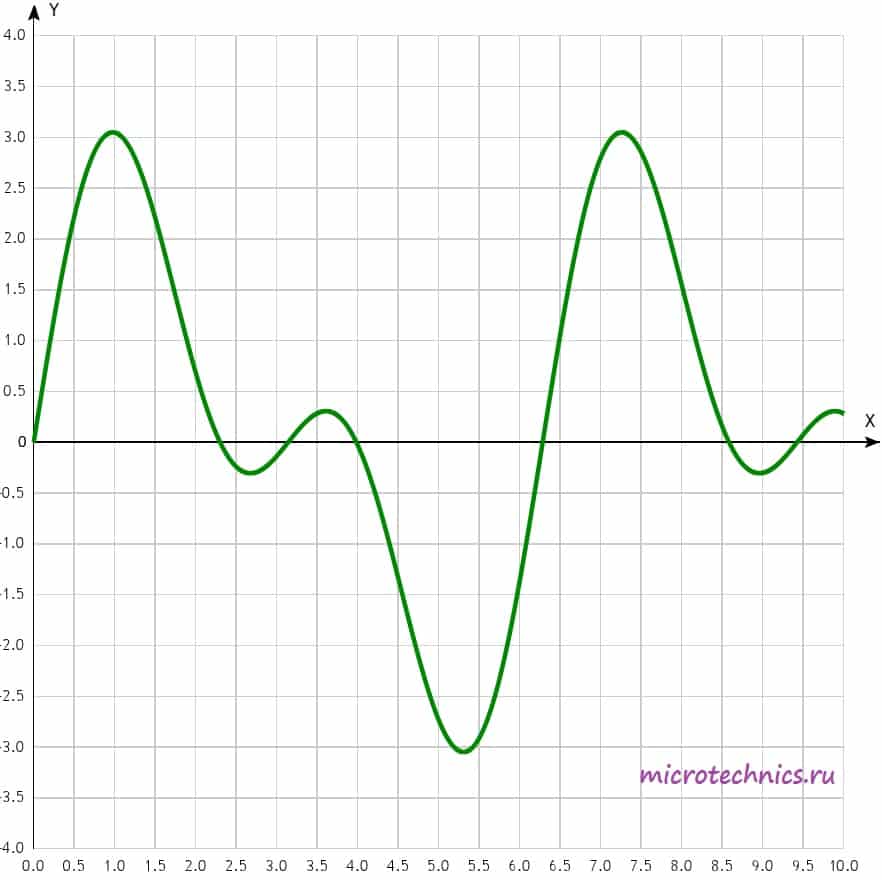
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:

Как видите, несмотря на «нестандартную» форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.

Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:

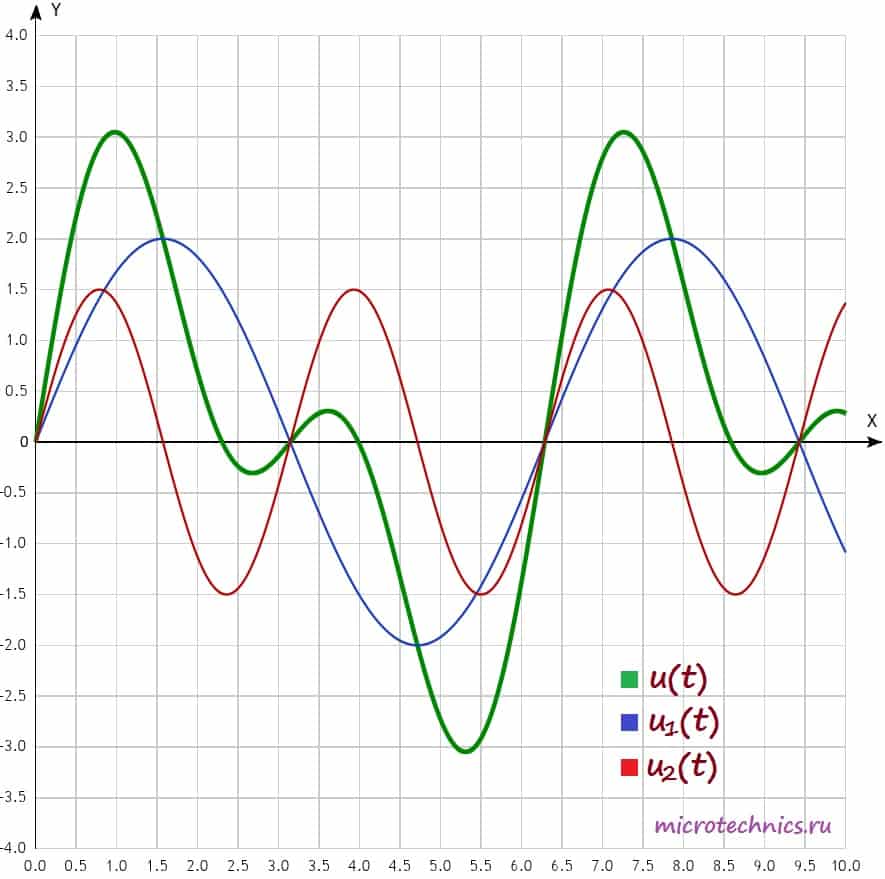
Давайте изобразим все эти сигналы на одном графике:

Функции u_1(t) , u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:

В этой формуле U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.

Амплитудный спектр сигнала.

Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:

• фазовый спектр сигнала — совокупность начальных фаз всех гармоник
• амплитудный спектр сигнала — амплитуды всех гармоник, из которых складывается негармонический сигнал

Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:

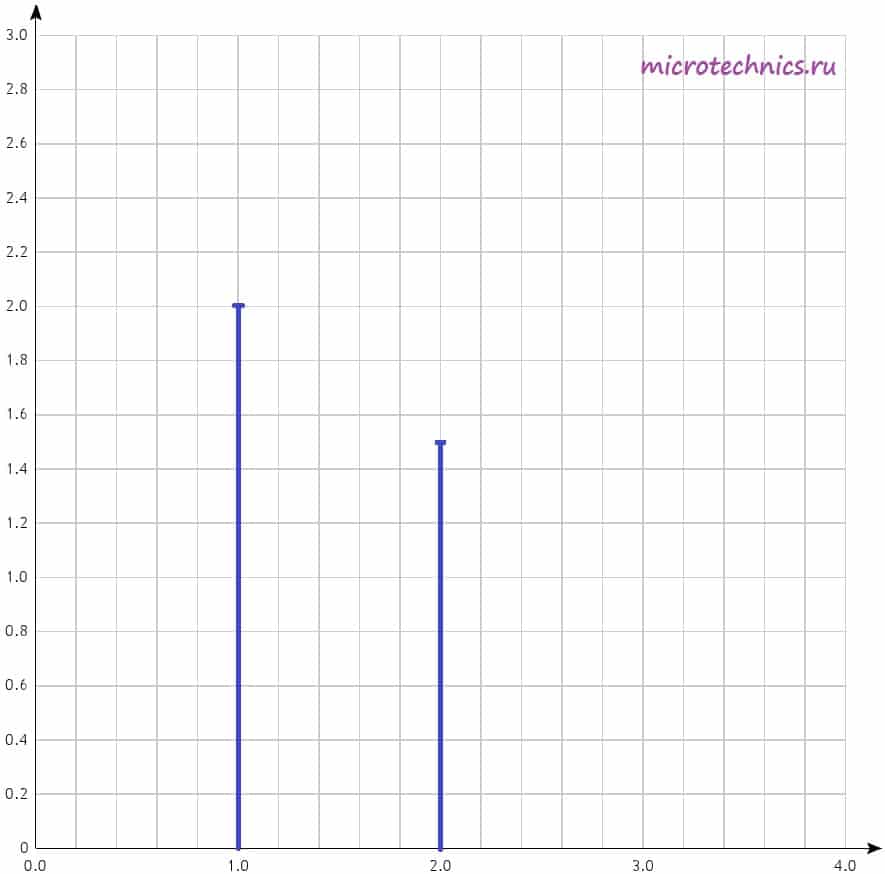
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:

У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.

Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.

Амплитудно-частотная характеристика (АЧХ).

АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?

АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:

Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.

Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…

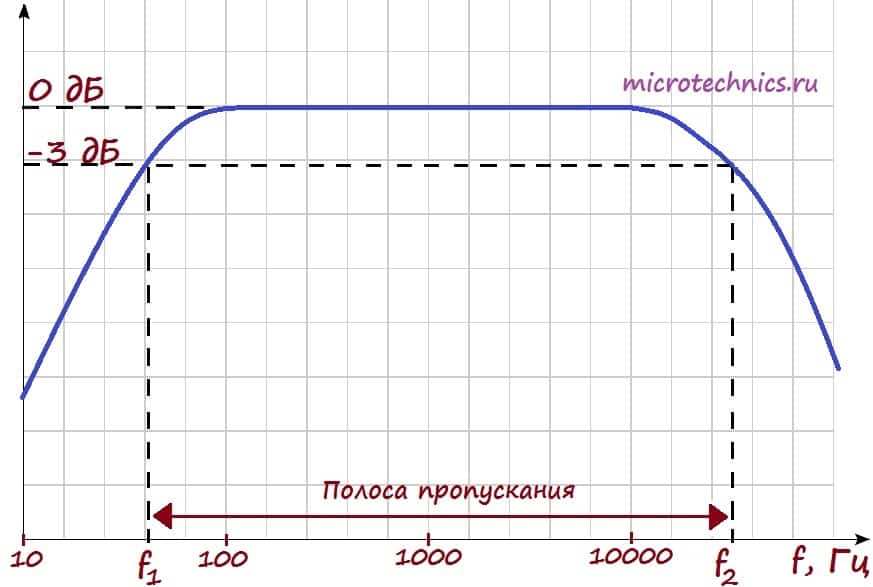
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:

Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.

По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.

На графике отдельно отмечены частоты f_1 и f_2 . Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация — сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.

Практические примеры АЧХ аудио-устройств.

Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:

• 20 Гц — 160 Гц — область низких частот
• 160 Гц — 1.28 КГц — область средних частот
• 1.28 КГц — 20.5 КГц — область высоких частот

Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂

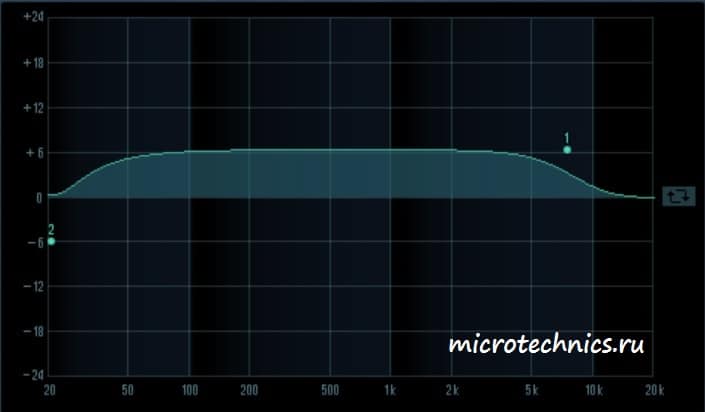
В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:

Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.

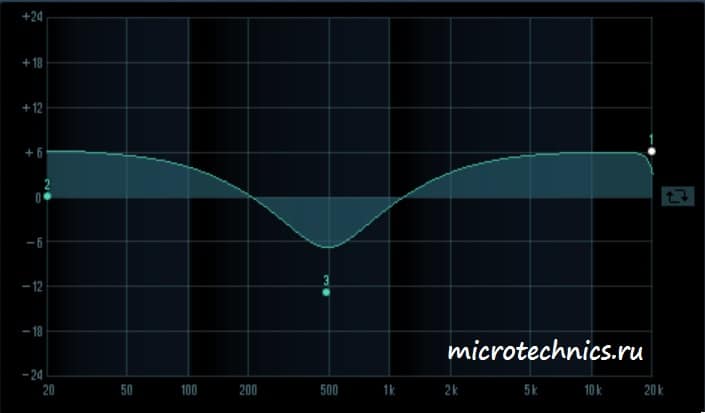
А здесь ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.

А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂

На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!

Источник