Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: 
ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине: А.
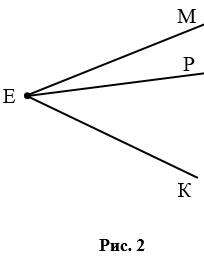
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
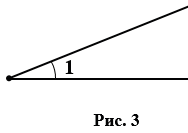
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 АОВ и ВОС — прямые, АОС — развернутый.
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый.
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой.
Поделись с друзьями в социальных сетях:
Источник
Соответственные углы
Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.
Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.
При пересечении двух прямых секущей образуется четыре пары соответственных углов.
∠1 и ∠5
∠2 и ∠6
∠3 и∠7
∠4 и ∠8
— соответственные углы при прямых a и b и секущей c.
Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
∠1 = ∠2
(как соответственные углы при при a ∥ b и секущей c).
Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 =∠8
Признак параллельных прямых
Если соответственные углы равны, то прямые параллельны.
∠1 = ∠2
А так как эти углы — соответственные при прямых при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.
Источник
Центральные и вписанные углы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
- Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается и половине градусной меры центрального угла, опирающегося на эту же дугу.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − ⌒AC − ⌒CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ ⌒AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ ⌒AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
⌒СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от ⌒CB = 72° / 2 = 36°
Источник
