Что значит сонаправлен с этой осью

§ 3. Определение координаты движущегося тела

В предыдущем параграфе говорилось о том, что положение тела, совершившего некоторое перемещение, можно найти графически, отложив вектор перемещения от начального положения этого тела. Но в большинстве случаев необходимо вычислить положение тела, т. е. определить его координаты.

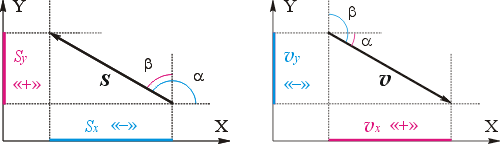
Известно, что вычисления производят не с векторами, а с соответствующими им скалярными величинами: с проекциями векторов на координатные оси и с модулями векторов или их проекций (т. е. с величинами, представляющими собой положительные или отрицательные числа, но не имеющими направления).

Покажем, как определить координату движущегося тела, зная координату его начального положения и вектор перемещения. Для этого решим задачу.

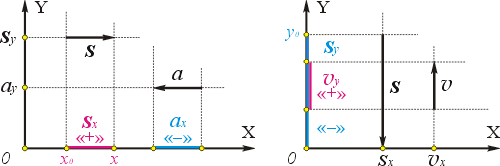
Два катера идут по реке в противоположных направлениях и встречаются в 100 км к востоку от пристани П (рис. 4). Продолжая движение, за некоторый промежуток времени t первый катер переместился от места встречи на 60 км к востоку, а второй — на 50 км к западу. Определите координаты каждого катера относительно пристани и расстояние между катерами через промежуток времени t после их встречи.

Проведём координатную ось ОХ параллельно прямой, вдоль которой движутся катера, и направим её на восток. Начало этой оси (х = 0) — точку О — совместим с пристанью, приняв её за тело отсчёта (поскольку в задаче требуется определить положение катеров по отношению к пристани).

Спроецировав начала и концы векторов перемещения и на ось ОХ, получим отрезки s_1x и s_2x, которые являются проекциями указанных векторов. Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси.

Значит, в данном случае s_1x > 0, a s_2x 0. Значит, х₀ = 100 км.

Поскольку ось ОХ параллельна векторам перемещений катеров, длины проекций s_1x;c и s_2x равны соответственно длинам векторов и (как противоположные стороны построенных на них прямоугольников). А это означает, что модуль каждой проекции равен модулю соответствующего ей вектора.

Указанные в задаче расстояния (60 км и 50 км), на которые сместились катера за время t, представляют собой модули векторов их перемещений. Значит, модуль проекции s_1x равен 60 км, а модуль проекции s_2x равен 50 км.

Поскольку проекция s_1x положительна, то можно записать: s_1x = 60 км. Но проекция s_2x отрицательна, поэтому s_2x = -50 км.

Теперь запишем условие задачи и решим её.

Вопросы

1. С какими величинами производят вычисления — с векторными или скалярными?
2. При каком условии проекция вектора на ось будет положительной, а при каком — отрицательной?
3. Запишите уравнение, с помощью которого можно определить координату тела, зная координату его начального положения и вектор перемещения.

Упражнение 3

1. Мотоциклист, переехав через мост, движется по прямолинейному участку дороги. У светофора, находящегося на расстоянии 10 км от моста, мотоциклист встречает велосипедиста. За 0,1ч с момента встречи мотоциклист перемещается на 6 км, а велосипедист — на 2 км от светофора (при этом оба они продолжают двигаться прямолинейно в противоположных направлениях).

Определите координаты мотоциклиста и велосипедиста и расстояние между ними спустя 0,1ч после их встречи.

У к а з а н и е: начертите ось X, направив её в сторону движения мотоциклиста и приняв за тело отсчёта мост. Обозначьте на этой оси координату светофора (х_с), координаты велосипедиста (х_в) и мотоциклиста (х_м), которые они имели через 0,1ч после встречи. Над осью начертите и обозначьте векторы перемещений велосипедиста и мотоциклиста , а на оси — проекции этих векторов (s_вх и s_мx).

2. Мальчик держит в руках мяч на высоте 1 м от поверхности земли. Затем он подбрасывает мяч вертикально вверх. За некоторый промежуток времени t мяч успевает подняться на 2,4 м от своего первоначального положения, достигнув при этом точки наибольшего подъёма, и опуститься от этой точки на 1,25 м (рис. 5).

Пользуясь этим рисунком, определите: а) координату х₀ начального положения мяча; б) проекцию s_tx вектора перемещения , совершённого мячом за время t; в) координату х_t, которую имел мяч через промежуток времени t после броска.

Источник

Что значит сонаправлен с этой осью

Учебник Физика 7 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 страниц вышел из печати в июле 2015 г. в пятом издании. Учебник физики 7 класса рассчитан на 2 урока в неделю и содержит 6 тем курса физики, которые перечислены ниже.

Физика 7 класс, тема 01. Физические величины (7+2 ч)
Физика. Физическая величина. Измерение физических величин.
Цена делений шкалы прибора. Погрешность прямых и косвенных измерений.
Формулы и вычисления по ним. Единицы физических величин.
Метод построения графика. Физика 7 класс, тема 02. Масса и плотность (8+1 ч)
Явление тяготения и масса тела. Свойство инертности и масса тела.
Плотность вещества. Таблицы плотностей некоторых веществ.
Средняя плотность тел и их плавание.
Метод научного познания. Физика 7 класс, тема 03. Силы вокруг нас (13+2 ч)
Сила и динамометр. Виды сил.
Уравновешенные силы и равнодействующая.
Сила тяжести и вес тела. Сила упругости и сила трения.
Закон Архимеда. Вычисление силы Архимеда.
Простые механизмы. Правило равновесия рычага. Физика 7 класс, тема 04. Давление тел (10+0 ч)
Определение давления. Давление жидкости. Закон Паскаля. Давление газа.
Атмосферное давление. Барометр Торричелли. Барометр-анероид.
Вакуумметры. Манометры: жидкостные и деформационные.
Пневматические и гидравлические механизмы. Физика 7 класс, тема 05. Работа и энергия (9+1 ч)
Механическая работа. Коэффициент полезного действия. Мощность.
Энергия. Кинетическая и потенциальная энергия.
Механическая энергия. Внутренняя энергия.
Взаимные превращения энергии. Физика 7 класс, тема 06. Введение в термодинамику (15+2 ч)
Температура и термометры. Количество теплоты и калориметр.
Теплота плавления/кристаллизации и парообразования/конденсации.
Первый закон термодинамики. Двигатель внутреннего сгорания.
Теплота сгорания топлива и КПД тепловых двигателей.
Теплообмен. Второй закон термодинамики.

Учебник Физика 8 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в четвёртом издании. Учебник физики 8 класса рассчитан на 2 урока в неделю и содержит 5 тем курса физики, которые перечислены ниже.

Физика 8 класс, тема 07. Молекулярно-кинетическая теория (8+1 ч)
Из истории МКТ. Частицы вещества. Движение частиц вещества.
Взаимодействие частиц вещества. Систематизирующая роль МКТ.
Кристаллические тела. Аморфные тела. Жидкие тела. Газообразные тела.
Агрегатные превращения. Насыщенный пар. Влажность воздуха. Физика 8 класс, тема 08. Электронно-ионная теория (8+1 ч)
Строение атомов и ионов. Электризация тел и заряд.
Объяснение электризации. Закон сохранения электрического заряда.
Электрическое поле. Электрический конденсатор. Электрический ток.
Электропроводность жидкостей, газов и полупроводников. Физика 8 класс, тема 09. Постоянный электрический ток (13+2 ч)
Электрическая цепь. Сила тока. Электрическое напряжение. Работа тока.
Закон Ома для участка цепи. Сопротивление соединений проводников.
Закон Джоуля-Ленца. Электронагревательные приборы.
Полупроводниковые приборы. Переменный ток. Физика 8 класс, тема 10. Электромагнитные явления (8+1 ч)
Магнитное поле. Соленоид и электромагнит. Постоянные магниты.
Действие магнитного поля на ток. Электродвигатель на постоянном токе.
Электромагнитная индукция. Электротрансформатор. Передача электроэнергии.
Электродвигатель на переменном токе. Физика 8 класс, тема 11. Колебательные и волновые явления (9+2 ч)
Период, частота и амплитуда колебаний. Нитяной и пружинный маятники.
Механические волны. Свойства механических волн. Звук.
Электромагнитные колебания. Излучение и прием электромагнитных волн.
Свойства электромагнитных волн. Принципы радиосвязи и телевидения.

Учебник Физика 9 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в третьем издании. Учебник физики 9 класса рассчитан на 2 урока в неделю и содержит 4 темы курса физики, которые перечислены ниже.

Физика 9 класс, тема 12. Введение в кинематику (16+2 ч)
Что такое кинематика. Относительность движения. Путь и перемещение.
Сложение и вычитание векторов. Проекции векторов на координатные оси.
Равномерное движение. Мгновенная скорость. Равноускоренное движение.
Графическое описание движений. Равномерное движение по окружности. Физика 9 класс, тема 13. Введение в динамику (13+2 ч)
Что такое динамика. Первый, второй и третий законы Ньютона.
Законы Гука и Кулона-Амонтона. Закон всемирного тяготения.
Закон сохранения импульса. Реактивное движение.
Кинетическая энергия. Потенциальная энергия. Физика 9 класс, тема 14. Введение в оптику (11+1 ч)
Источники света. Прямолинейное распространение света. Отражение света.
Зеркала. Преломление света. Линзы. Оптические приборы.
Дисперсия света и цвета тел. Фотография и полиграфия.
Корпускулярно-волновой дуализм. Физика 9 класс, тема 15. Введение в квантовую физику (7+1 ч)
Физика XX века. Явление радиоактивности. Регистрация частиц.
Строение атома. Характеристики атомного ядра. Ядерные реакции.
Природа и свойства радиоактивных излучений. Энергия связи ядра.
Энергия ядерных реакций. Ядерная энергетика. Физика XXI века.

Для перехода к параграфам кликайте нумерацию 01 02 03 04 05 и т.д. вверху страницы. Параграфы каждой темы курса физики снабжены интерактивными вопросами и заданиями.

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Источник

Проекции векторов на координатные оси

Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.

Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.

На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:

sx = s · cos(α) = 50 км · cos( 150°) = –43 км

Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:

sy = s · cos(β) = 50 км · cos( 60°) = +25 км

Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.

На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:

υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c

Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.

Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.

Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .

Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .

На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.

Источник