Что значит соединить точки попарно отрезками

Содержание

Учимся расчерчиванию
Учимся расчерчиванию
Мерзляк 5 класс — § 3. Отрезок. Длина отрезка
Вопросы к параграфу
Решаем устно
Упражнения
Упражнения для повторения
Задача от мудрой совы

Учимся расчерчиванию

Сегодняшняя тема » расчерчивание«. Это замечательный способ развития глазомера и твердости руки. Из всех вариантов линий, которые можно провести от руки, пожалуй, прямая линия одна из самых сложных потому что не допускает вариантов: линия либо действительно прямая, либо нет.

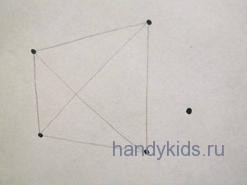
Начнём с освоения начертания коротких отрезков прямой линии. Перед нами лист с симметрично расположенными точками, которые соответственно нужно соединить попарно отрезками прямых линий.

Проводить линию сразу не советуем: вначале желательно для уверенности провести ее пальцем, затем – карандашом без нажима и затем уже, «набело» — с нажимом. Так советуем поступать и во всех последующих случаях при начертании линий от руки.

(Впрочем,эти же задания отлично можно применять и для освоения расчерчивания по линейке). Когда ребята справятся с этим первым заданием, усложним раздадим заготовки в которых несколько точек расположены не совсем симметрично.

Хотя никакой договорённости что точки обязательно симметричны не было, дети удивятся,что «правила»нарушены. Ладно,пусть поучатся не упираться в собственные свежеизобретённые стереотипы. Такие задания между прочим требуют нескольких закрепляющих повторений в течение года (варианты мы подскажем Подписывайтесь на обновления блога Handykids.ru -«Изо» и «ручной труд» для детей по почте] ).

Теперь раздадим заготовки с четырьмя точками. Задание: соединить каждую точку со всеми остальными. Изобразить четырехугольник смогут все, но не все догадаются провести еще и диагонали. Так и дадим детям возможность пошевелить мозгами. Ну,если уж никак не додумаются,то намёком подскажем. После этого можно задание усложнить, то есть добавить больше точек.

Последующие получаемые фигуры напоминают драгоценные камни. Поскольку наш девиз всегда был «получить от каждого задания максимум разнообразной пользы»,то и не будем ограничиваться только расчерчиванием. Предложим ученикам раскрасить эти самоцветы.

Подойдем к вопросу творчески, а заодно поучимся регулировать силу нажима на карандаш: пусть каждая «грань» камня будет иметь свою определенную тональность в рамках одного и того же цвета. Вот два весьма полезных варианта: либо раскрашивать все грани одним карандашом(у нас это красный)так, чтобы грани различались по тону(тоновый контраст). Либо поработать и с тоном и с оттенками цвета. Поупражняемся ещё и в цветоведении.

Понятно же,что в наборах карандаши имеют не строго спектральные цвета. Собрав все разнообразные оттенки зелёного изобразим разнообразно-зелёный изумруд.Кстати, дети сами по себе обычно не используют наложение цвета карандашей. Стоит показать этот приём, пусть уже осваивают.

Источник

Учимся расчерчиванию

Источник

Мерзляк 5 класс — § 3. Отрезок. Длина отрезка

Вопросы к параграфу

Сколько существует отрезков, концами которых являются две данные точки? — существует только один отрезок, концами которого являются две данные точки.
Как обозначают отрезок? — записывают точки, которые являются концами отрезка, например: АВ, МК и т.д.
Какие вы знаете единицы длины? — 1 мм (миллиметр), 1 дм (дециметр), 1 см (сантиметр), 1 м (метр), 1 км (километр).
Объясните, что означает измерить длину отрезка — это означает, что надо посчитать сколько единичных отрезков (единиц длинны) помещается в этом отрезке, например, сколько раз в нём помещается один сантиметр.
Каким свойством обладает длина отрезка? — если на отрезке АВ отметить точку С, то длина отрезка АВ будет равна сумме длин отрезков АС и СВ: АВ = АС + СВ.
Какие отрезки называют равными? — два отрезка называют равными, если они совпадают при наложении.
Какие длины имеют равные отрезки? — равные отрезки имеют равные длины.
Какой из двух неравных отрезков считают большим? — большим считают тот, у которого длина больше.
Что называют расстоянием между точками A и B? — длиной отрезка АВ.
Объясните, какую геометрическую фигуру называют ломаной — это фигура, состоящая из последовательно соединённых отрезков и в которой конец первого отрезка совпадает с началом второго, конец второго отрезка совпадает с началом третьего и т.д.
Что называют длиной ломаной? — сумму длин всех его звеньев (отрезков, из которых состоит ломанная.
Какую ломаную называют замкнутой? — замкнутой называют ломанную, конец последнего отрезка которой совпадает с началом первого отрезка.

Решаем устно

1. Реши:

Какое число больше числа 46 на 9? 46 + 9 = 55 — ответ 55
Какое число меньше числа 72 на 15? 72 — 15 = 57 — ответ 57
Какое число больше числа 21 в 7 раз? 21 • 7 = 147 — ответ 147
Какое число меньше числа 65 в 13 раз? 65 : 13 = 5 — ответ 5

2. Назовите все двузначные числа, сумма цифр которых равна 6.

60, 51, 15, 42, 24, 33

3. Назовите все двузначные числа, разность цифр которых равна 7.

4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырёхзначное число.

9 999, 10 000, 10 001

5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырёхзначное число.

6. Выразите в сантиметрах:

7 дм 4 см = 74 см
4 м 1 см = 401 см
2 м 6 дм = 260 см
1 м 2 дм 5 см = 125 см

7. Выразите в дециметрах и сантиметрах:

72 см = 7 дм 2 см
146 см = 14 дм 6 см
450 мм = 4 дм 5 см
8 м 40 мм = 80 дм 4 см

Упражнения

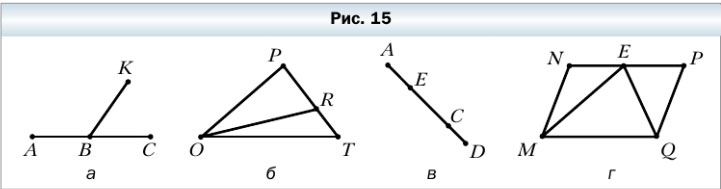
44. Запишите все отрезки, изображённые на рисунке 15.

б) OP, PR, RT, PT, TO, OR

в) AE, AC, AD, EC, ED, CD

г) MN, NE, NP, EP, PQ, QE, QM, EM

45. Запишите все отрезки, изображённые на рисунке 16.

а) BO, BD, OD, CO, CA, OA, AD

б) FK, FE, KE, EN, ES, NS, MK, MN, MP, KN, KP, NP

46. Отметьте в тетради точки А, В, С, D и соедините их попарно отрезками. Сколько отрезков образовалось? Сколько образовалось отрезков с концом в точке A?

Образовалось 6 отрезков с концами в данных точках: AB, AC, AD, BC, BD, CD.
Образовалось 3 отрезка с концом в точке А: AB, AC, AD.

Комментарий: новую точку на чертеже, образованную пересечением отрезков AC и BD мы не учитываем, поскольку о ней не говорится в задании.

Для того, чтобы образование 6 отрезков выглядело более наглядно, можно расположить заданные точки в следующем порядке:

Такое решение задания также является правильным.

47. Начертите отрезки MN и АС так, чтобы MN = 6 см 3 мм, АС = 5 см 4 мм.

48. Начертите отрезки EF и ВК так, чтобы EF = 9 см 2 мм, ВК = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрезка АС?

50. Начертите отрезок ТР, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

TP — TE = 7 см 8 мм — 2 см 6 мм = 5 см 2 мм

Ответ: 5 см 2 мм.

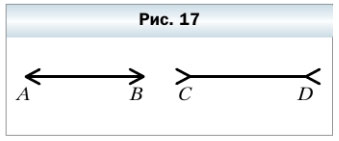
51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.

Глядя на рисунок 17 кажется, что отрезок CD > AB.

Проверим вывод измерением:

Ответ: эти отрезки равны.

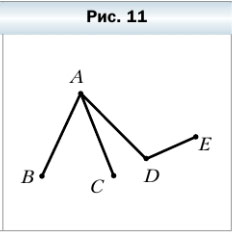
52. Назовите все ломаные, изображённые на рисунке 11. Какая из них имеет наибольшее количество звеньев?

На рисунке 11 можно выделить 5 ломаных:

BAC — 2 звена
BADE — 3 звена
ADE — 2 звена
CADE — 3 звена
CAD — 2 звена

Значит наибольшее количество звеньев имеют ломанные BADE и CADE.

53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

Назовём звенья ломанной и измерим их длину:

AB = 19 мм
BE = 18 мм
EK = 16 мм
KP = 11 мм
PR = 12 мм

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

AB + BE + EK + KP + PR = 19 + 18 + 16 + 11 + 12 = 76 (мм) — длина ломаной ABEKPR

Ответ: длина ломаной 76 мм.

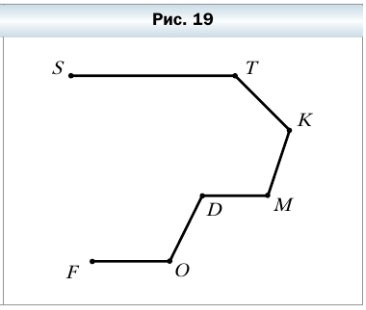
54. Запишите звенья ломаной, изображённой на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

Назовём звенья ломанной и измерим их длину:

ST = 27 мм
TK = 13 мм
KM = 11 мм
MD = 11 мм
DO = 12 мм
OF = 13 мм

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

ST + TK + KM + MD + DO + OF = 27 + 13 + 11 + 11 + 12 + 13= 87 (мм) — длина ломаной STKMDOF

Ответ: длина ломаной 87 мм .

55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клетки правее и на 1 клетку выше точки В; точку D — на 3 клетки правее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки А, В, С, D и Е. Какая фигура образовалась? Запишите её название и укажите количество звеньев.

Образовалась фигура ломаная ABCDE. Она состоит из 4 звеньев.

56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

AB + BC + CD + DE = 8 + 14 + 23 + 10 = 55 (см) — длина ломаной ABCDE.

Ответ: длина ломаной 55 см.

57. Вычислите длину ломаной MNKPEF, если MN= 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

MN + NK + KP + PE + EF = 42 + 38 + 19 + 12 + 29 = 140 (мм) — длина ломаной MNKPEF.

Ответ: длина ломаной 55 см.

58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.

Измерим длины звеньев ломаной:

AB + BC + CD = 18 + 30 + 36 = 84 (мм) — длина ломаной ABCD

Ответ: длина ломаной 84 мм.

59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.

34 • 3 = 102 (см) — длина отрезка SK.

34 + 102 = 136 (см) — длина отрезка RK.

Ответ: длина отрезка RK 136 см.

60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если AD = 135 см.

135 : 5 = 27 (см) — длина отрезка DB.

135 + 27 = 162 (см) — длина отрезка АВ.

Ответ: длина отрезка АВ 162 см.

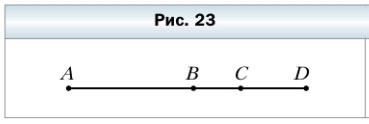
61. Известно, что АС = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

32 — 9 = 23 (см) — длина отрезка AB.

9 + 12 = 21 (см) — длина отрезка BD.

Ответ: AB = 23 см, BD = 21 см.

62. Известно, что MF= 43 см, ME = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.

26 — 18 = 8 (см) — длина отрезка MK.

43 — 26 = 17 (см) — длина отрезка EF.

Ответ: MK = 8 см, EF = 17 см.

63. Даны две точки А и В. Сколько можно провести отрезков, соединяющих эти точки? Сколько можно провести ломаных, соединяющих эти точки?

Через две данные точки А и В можно провести один и только одинотрезок, соединяющий эти точки.
Через две данные точки А и В можно провести бесконечное количество ломанных, соединяющих эти точки.

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

На рисунке образовались отрезки: MA, MC, MK, AC, AK, CK. Всего 6 отрезков.

65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому отрезку, причём точка К лежит между точками М и В, AM = 12 см, ВК = 9 см. Найдите длину отрезка МК.

28 — (12 + 9) = 28 — 21 = 7 (см) — длина отрезка MK.

66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрезка ВС? Есть ли в условии задачи лишние данные?

Так как по условию задачи АВ на 5 см больше отрезка АС, то есть AB — AC = 5 см, то BC = 5 см.

Фраза «длина отрезка АС равна 15 см» является лишней в условии задачи, поскольку длина отрезка BC будет равна 5 см независимо от значения длины отрезка АС.

Ответ: 5 см, да «длина отрезка АС равна 15 см» — лишние данные.

67. Отрезки MT и FK равны (рис. 25). Сравните отрезки MF и ТК.

По условию MT = FK. Значит можно записать уравнение:

68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.

ACDM = АС + CD + DM

15 + 24 + 32 = 71 (мм) — длина ломаной ACDM.

69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.

EF = 8 + 14 = 22 мм

FK = 22 — 7 = 15 мм

CEFK = CE + EF + FK

8 + 22 + 15 = 45 (мм) — длина ломаной CEFK.

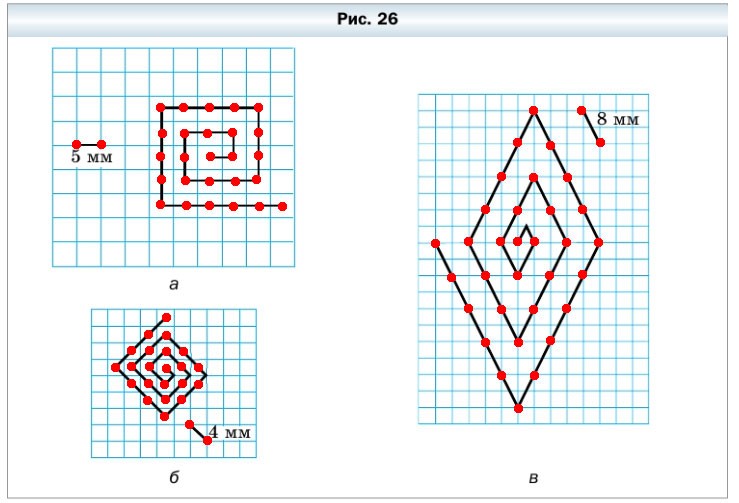
70. Вычислите длину ломаной, изображённой на рисунке 26.

Разделим ломаные на единичные отрезки равные заданному и посчитаем их количество.

а) ломаную можно разделить на 25 отрезков, равных заданному. Длина заданного отрезка 5 мм, значит длина ломаной: 5 • 25 = 125 мм.
б) ломаную можно разделить на 21 отрезок, равных заданному. Длина заданного отрезка 4 мм, значит длина ломаной: 4 • 21 = 84 мм.
в) ломаную можно разделить на 31 отрезок, равный заданному. Длина заданного отрезка 8 мм, значит длина ломаной 8 • 31 = 248 мм.

Ответ: 125 мм, 84 мм и 248 мм.

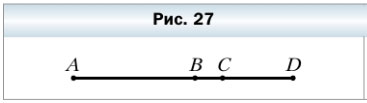
71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.

8 — 2 = 6 (см) — длина отрезка AB.

6 + 6 = 12 (см) — длина отрезка AD.

Ответ: AD = 12 см.

72. Известно, что MF= 30 см, ME = 18 см, KF = 22 см (рис. 28). Найдите длину отрезка КЕ.

30 — 18 = 12 (см) — длина отрезка EF.

22 — 12 = 10 (см) — длина отрезка KE.

Ответ: KE = 10 см.

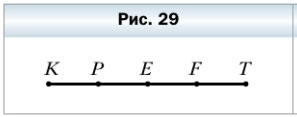
73. Известно, что KP = PE = EF= FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.

На рисунке 29 можно найти следующие равные отрезки:

74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?

Если на отрезке отметить семь точек на равном расстоянии, то получится 6 равных отрезков. Это значит, что на первом отрезке будет отмечено 6 отрезков по 3 см, а длина первого отрезка будет равна: 3 • 6 = 18 см.
Если на отрезке отметить десять точек на равном расстоянии, то получится 9 равных отрезков. Это значит, что на втором отрезке будет отмечено 9 отрезков по 2 см, а длина второго отрезка будет равна: 2 • 6 = 18 см.

Это значит, что расстояние между крайними точками у первого и второго отрезка будет одинаковым.

Проверим вывод графически:

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = MС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

Для удобства обозначим равные отрезки отдельными цветами.

1) Известно, что МК = 4 см.

МК = MС + СК = 4 см

2) Известно, что ВМ = MС и KD = СК . Значит:

ВМ + KD = MС + СК = 4 см

3) ВD = ВМ + MС + KD + СК = ( ВМ + KD) + ( MС + СК) = 4 + 4 = 8 см

4) Мы знаем, что АЕ = 12 см, ВD = 8 см.

AQ + QB + DR + RE = АЕ — ВD = 12 — 8 = 4 см

5) Известно, что AQ = QB и DR = RE . Значит:

AQ + RE = QB + DR = 4 : 2 = 2 см

6) QR = АЕ — ( AQ + RE ) = 12 — 2 = 10 см

Ответ: QR = 10 см.

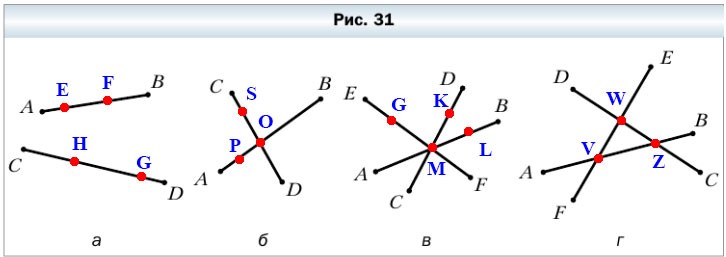
76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них были две отмеченные точки, не считая концов отрезков?

а) Надо отметить 4 точки: две на отрезке AB (например E и F) и две на отрезке CD (например H и G).

б) Надо отметить 3 точки: точку пересечения отрезков CD и AB (точка O) и по одной точке на отрезке CD (например точку S) и на отрезке AB (например P).

в) Надо отметить 4 точки: точку пересечения отрезков EF, AB и CD (точка M), а также по одной точке на отрезке EF (например G), отрезке AB (например точку L) и отрезке CD (например K).

г) Надо отметить 3 точки: точку пересечения отрезков DC и FE (точка W), точку пересечения отрезков AB и FE (точка V) и точку пересечения отрезков AB и DC (точка Z).

77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может построить отрезок длиной:

1) 3 см — Миша должен начертить отрезок 13 см, а потом от одной из конечных точек два раза отмерить по 5 см:

13 — 5 • 2 = 13 — 10 = 3 (см)

2) 2 см — Миша должен три раза отмерить отрезки по 5 см, а потом вычесть из полученного большого отрезка отрезок 13 см:

5 • 3 — 13 = 15 — 13 = 2 (см)

3) 1 см — Миша должен два раза отмерить отрезки по 13 см, а потом из полученного большого отрезка вычесть пять раз по 5 см:

13 • 2 — 5 • 5 = 26 — 25 = 1 (см)

Упражнения для повторения

78. Вычислите:

79. Выполните действия:

80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограммов больше подарили конфет, чем печенья?

1) 5 • 4 = 20 (кг) — конфет подарили.

2) 3 • 6 = 18 (кг) — печенья подарили.

3) 20 — 18 = 2 (кг) — конфет больше, чем печенья.

Ответ: конфет подарили больше на 2 кг.

81. Медведица Настасья Петровна заготовила на зиму 7 бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасья Петровна?

1) 12 • 7 = 84 (кг) — мёда в 12-ти килограммовых бочонках.

2) 10 • 8 = 80 (кг) — мёда в 10-ти килограммовых бочонках.

3) 84 + 80 = 164 (кг) — мёда заготовила Настасья Петровна.

82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть привезённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

1) 240 + 156 = 396 (кг) — фруктов завезли.

2) 396 : 3 = 132 (кг) — фруктов продали в 1 день.

3) 396 — 132 = 264 (кг) — фруктов продали во 2 день.

83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского сада, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?

1) 246 + 354 = 600 (кг) — фруктов вырастил Кот Матроскин.

2) 600 : 6 = 100 (кг) — фруктов отдал в детский сад.

3) 600 : 5 = 120 (кг) — фруктов отдал в школу.

4) 600 — (100 + 120) = 600 — 220 = 380 (кг) — фруктов отдал в больницу.

Задача от мудрой совы

84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.

Для того, чтобы в искомом натуральном числе было наименьшее количество цифр найдём максимальное количество цифр 9 (самая большая цифра), которые мы сможем использовать:

99 : 9 = 11 — девяток можно использовать.

Далее найдём оставшуюся цифру, необходимую для того, чтобы сумма цифр искомого числа равнялась 101:

101 — 9 • 11 = 101 — 99 = 2 — оставшаяся цифра искомого числа.

Это значит, что в искомом натуральном числе одна цифра 2 и одиннадцать цифр 9. Теперь расположим цифры так, чтобы натуральное число было наименьшим.

299 999 999 999 — на место сотен миллиардов поставим самую маленькую цифру.

Источник

Читайте также: Великая цель что значит