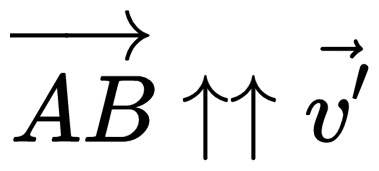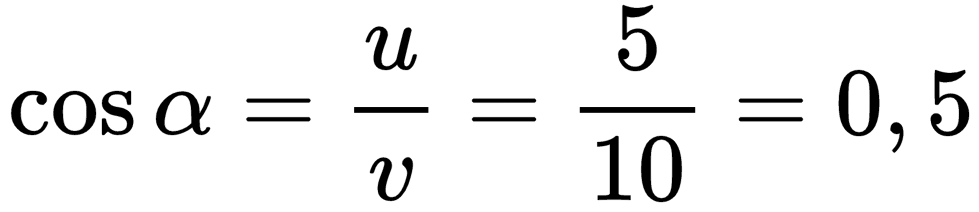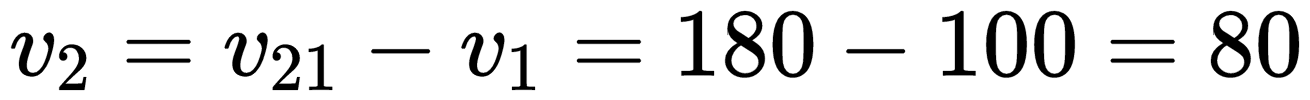Что значит скорость относительна приведите пример

§ 9. Относительность движения. —

Вопросы.

1. Что означают следующие утверждения: скорость относительна, траектория движения относительна, путь относителен?

Это означает, что эти величины (скорость, траектория и путь) для движения различаются в зависимости от того, из какой системы отсчета ведется наблюдение.

2. Покажите на примерах, что скорость, траектория движения и пройденный путь являются относительными величинами.

Например, человек стоит неподвижно на поверхности Земли (нет ни скорости, ни траектории, ни пути), однако в это время Земля вращается вокруг своей оси, и следовательно человек, относительно, например центра Земли, движется по определенной траектории (по окружности), перемещается и имеет определенную скорость.

3. Сформулируйте коротко, в чем заключается относительность движения.

Движение тела (скорость, путь, траектория) различны в разных системах отсчета.

4. В чем основное отличие гелиоцентрической системы от геоцентрической?

В гелиоцентрической системе тело отсчета- Солнце, а в геоцентрической- Земля.

5. Объясните смену дня и ночи на Земле в гелиоцентрической системе (см. рис. 18).

В гелиоцентрической системе смена дня и ночи объясняется вращением Земли.

1. Вода в реке движется со скоростью 2 м/с относительно берега. По реке плывёт плот. Какова скорость плота относительно берега? относительно воды в реке?

Скорость плота относительно берега — 2 м/с, относительно воды в реке — 0 м/с.

2. В некоторых случаях скорость тела может быть одинаковой в разных системах отсчёта. Например, поезд движется с одной и той же скоростью в системе отсчета, связанной со зданием вокзала, и в системе отсчёта, связанной с растущим у дороги деревом. Не противоречит ли это утверждению о том, что скорость относительна? Ответ поясните.

Если оба тела, с которыми связаны системы отсчета этих тел, остаются неподвижными друг относительно друга, то они связаны с третьей системой отсчета — Землёй, относительно которой и происходят измерения.

3. При каком условии скорость движущегося тела будет одинакова относительно двух систем отсчета?

Если эти системы отсчета неподвижны относительно друг друга.

4. Благодаря суточному вращению Земли человек, сидящий на стуле в своём доме в Москве, движется относительно земной оси со скоростью примерно 900 км/ч. Сравните эту скорость с начальной скоростью пули относительно пистолета, которая равна 250 м/с.

5. Торпедный катер идет вдоль шестидесятой параллели южной широты со скоростью 90 км/ч по отношению к суше. Скорость суточного вращения Земли на этой широте равна 223 м/с. Чему равна в (СИ) и куда направлена скорость катера относительно земной оси, если она движется на восток? на запад?

Источник

Относительная скорость

Относительная скорость – скорость объекта В относительно А. Отображается как vAB, где А – скорость в покое В.

Галилей наблюдал концепцию сложного движения при помощи мухи и лодки. Он заметил: на борту лодки можно измерить скорость полета мухи (u). Затем можно вернуться на землю и вычислить скорость лодки (v). Но является ли скорость u фактической? Нет, потому что вы вычисляли скорость относительно лодки. Чтобы получить скорость относительно берега (s), можно использовать векторную сумму: s = u + v.

Примеры относительной скорости

Давайте рассмотрим примеры относительной скорости. Вообразите, что сидите в пассажирском поезде, отправляющимся в восточном направлении. Если посмотреть в окно и увидеть, что человек идет в ту же сторону, то покажется, что он перемещается намного медленнее. А теперь покинем поезд и посмотрим на мужчину снаружи. Сейчас кажется, что он идет вдвое быстрее, чем раньше.

Переместимся в лодку. На берегу человек шагает от одного бревна к другому. Скорость относительно берега будет обычной и ничем не выделяться. Но теперь вы оказались на берегу, а человек идет между двумя точками, но по движущейся лодке. Кажется, что его скорость намного быстрее.

Как так? Относительная скорость связана с системой координат. В случае с поездом, она двигалась в ту же сторону, что и человек, поэтому вызывала эффект замедления. Однако в неподвижной точке фиксируется реальный показатель. То же самое повторяется и с примером в лодке.

Источник

Относительная скорость.

Относительная скорость – это физическая величина, равная векторной разности скоростей, заданных относительно неподвижной системы отсчета.

При изучении механического движения в первую очередь подчеркивается его относительность. При изучении различных свойств движения тела предполагается, что рассматривается абсолютное движение (т. е. движение, отнесенное к неподвижным осям). Во многих случаях возникает необходимость определить относительное движение, отнесенное к системе отсчета, движущейся по отношению к неподвижным осям.

Относительное движение точки по отношению к подвижной системе отсчета может рассматриваться как абсолютное движение, и обладает всеми свойствами абсолютного движения.

Движение можно рассматривать в разных системах отсчета. Выбор системы отчета диктуется удобством: ее нужно выбрать так, чтобы изучаемое движение и его закономерности выглядели по возможности проще. Для перехода от одной системы отсчета к другой необходимо знать, какие характеристики движения изменяются и каким образом, а какие остаются неизменными.

Исходя из опытов можно утверждать, что при рассмотрении движений, происходящих со скоростями, малыми по сравнению со скоростью света, время неизменно во всех системах отсчета, что означает, что при измерении в любой системе отсчета промежуток времени между двумя событиями одинаков.

Что же касается пространственных характеристик, то положение тела изменяется при переходе к другой системе отсчета, однако при этом не меняется пространственное расположение этих двух событий.

Теперь рассмотрим изменение скорости движения тел при переходе от одной системы отсчета к другой, которая движется относительно первой.

Рассмотрим пример переправы на пароме, движущемся поступательно относительно берегов (относительно земли). Вектор перемещения пассажира относительно берегов обозначим через Δr, а относительно парома – через Δr´. Перемещение парома относительно земли за то же время Δt обозначим через ΔR. В этом случае

Разделим равенство почленно на промежуток времени Δt, в течение которого произошли эти перемещения. Перейдя к пределу Δt >0, получим аналогичное соотношение для скоростей:

где υ – скорость пассажира относительно земли, V – скорость парома относительно земли, υ´ — скорость пассажира относительно парома. Этим равенством выражается правило сложения скоростей, которое при одновременном участии тела в двух движениях можно трактовать как закон преобразования скорости тела при переходе от одной системы отсчета к другой. На самом деле, υ и υ´ — скорости пассажира в двух разных системах отсчета, а V – скорость одной системы (парома) относительно другой (земли).

Из формулы (2) следует, что относительная скорость двух тел одинакова во всех системах отсчета. При переходе к новой системе отсчета к скорости каждого тела прибавляется один и тот же вектор V скорости системы отсчета. Поэтому разность векторов скоростей тел υ – υ´ не изменяется. Относительная скорость тел абсолютна.

Источник

Относительность механического движения

теория по физике 🧲 кинематика

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ — перемещение МТ относительно НСО, s ₁— перемещение МТ относительно ПСО, s ₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0,перемещение s′ = s₂
• Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0,перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0,скорость v′ = u
• Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0,скорость v′ = u

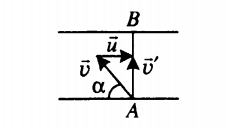
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v _отн — относительная скорость, или скорость первого тела относительно второго, v ₁ и v ₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

• v ₁₂ — скорость первого тела относительно второго. Ее проекция равна:

• v ₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x — v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

• Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

• Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

• Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b . Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
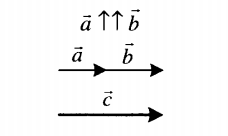	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
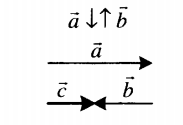	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
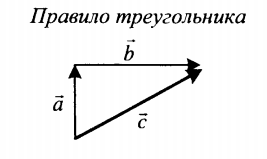
Сложение двух векторов, расположенных друг к другу под углом
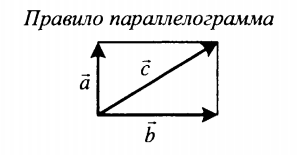
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .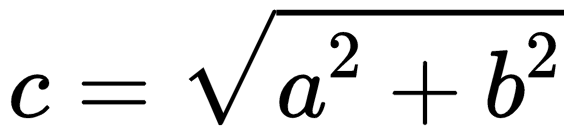
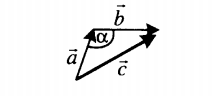	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .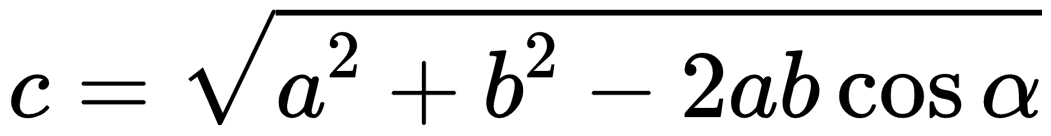
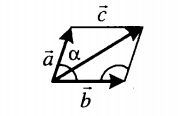	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .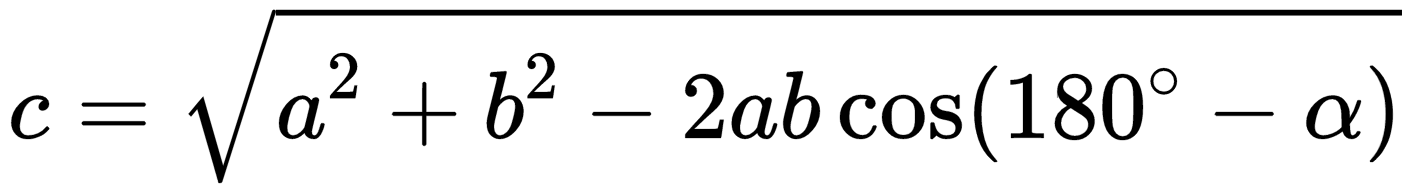

Правила вычитания векторов

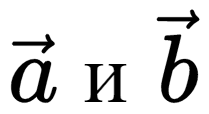
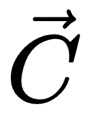
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
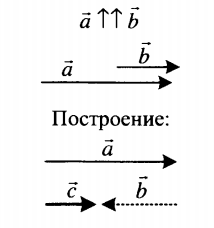	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|.
Вычитание двух противоположно направленных векторов
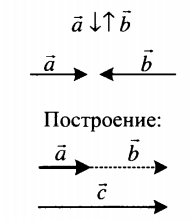	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
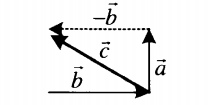	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .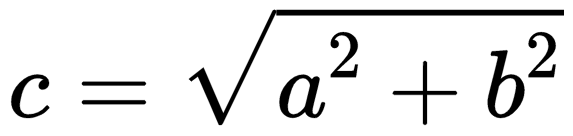
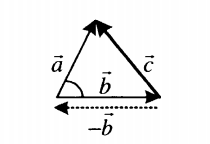	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .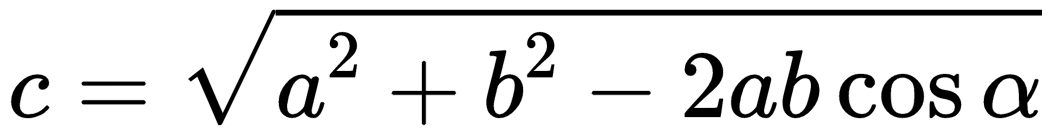

Два автомобиля движутся по прямому шоссе, первый — со скоростью v , второй — со скоростью –4 v . Найти скорость второго автомобиля относительно первого.

Алгоритм решения

1. Записать данные в определенной системе отсчета.
2. Изобразить графическую модель ситуации задачи.
3. Записать классический закон сложения скоростей в векторном виде.
4. Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
5. Найти искомую величину.

Решение

Записываем данные относительно Земли:

• Скорость первого автомобиля относительно оси ОХ: v ₁ = v .
• Скорость второго автомобиля относительно оси ОХ: v ₂ = –4 v .

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник