Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
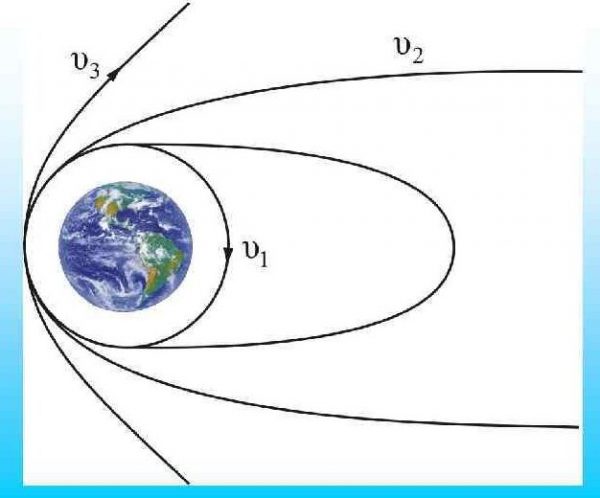
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
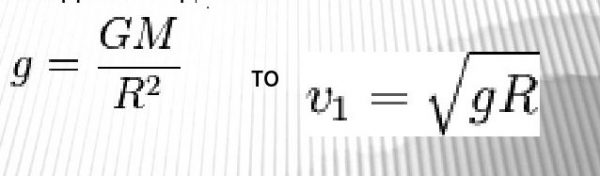
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
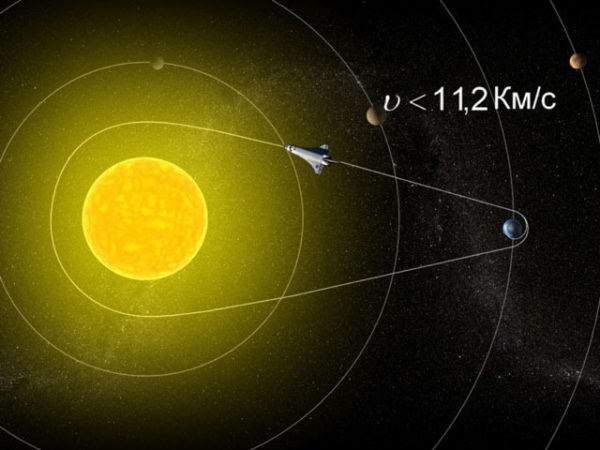
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник
Орбитальная скорость
Орбитальная скорость тела (обычно планеты, естественного или искусственного спутника, кратной звезды) — это скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.
Определение
В полярных координатах выражение для орбитальной скорости (
— гравитационный параметр, равный G(M+m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела
— фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение
— для эллипса и гиперболы)
— эксцентриситет (
для эллипса,
для параболы,
— для гиперболы)
— истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела
Орбитальная скорость также может вычисляться по следующим формулам:
- в общем виде:
- для эллиптической орбиты:
- параболическая траектория:
- гиперболическая траектория:
- для эллиптической орбиты:
— гравитационный параметр
— расстояние между вращающимся телом и центральным телом
—удельная орбитальная энергия
— длина большой полуоси
- эллиптические скорости
соответствуют движению по эллиптическим траекториям
- частным случаем эллиптической скорости является круговая, или первая космическая скорость
- параболическая скорость
соответствует движению по параболической траектории и называется так же второй космической скоростью
- гиперболические скорости
\sqrt<\mu\left(<2\over
>\right)>» border=»0″/> соответствуют движению по гиперболическим траекториям
Орбиты Земли
| Орбита | Расстояние между центрами масс | Высота над поверхностью Земли | Орбитальная скорость | Орбитальный период | specific orbital energy (англ.) |
|---|---|---|---|---|---|
| Поверхность Земли, для сравнения | 6,400 км | 0 км | 7.89 км/с | — | -62.6 MJ/kg |
| Низкая опорная орбита | 6,600 — 8,400 км | 200 — 2,000 км | Круговая орбита: 6.9 — 7.8 км/с эллиптическая орбита: 6.5 — 8.2 км/с | 89 — 128 мин | -17.0 MJ/kg |
| Высокоэллиптическая орбита спутников Молния | 6,900 — 46,300 км | 500 — 39,900 км | 1.5 — 10.0 км/с | 11 ч 58 мин | -4.7 MJ/kg |
| Геостационарная орбита | 42,000 км | 35,786 км | 3.1 км/с | 23 ч 56 мин | -4.6 MJ/kg |
| Орбита Луны | 363,000 — 406,000 км | 357,000 — 399,000 км | 0.97 — 1.08 км/с | 27.3 дней | -0.5 MJ/kg |
Примечания
- ↑Балк М. Б. Скорость спутника и её компоненты // Элементы динамики космического полета. — М .: Наука, 1965. — С. 61—62. — 340 с. — (Механика космического полета).
| Основные | Box-орбита • Орбита захвата • Эллиптическая орбита / Высокая эллиптическая орбита • Орбита ухода • Орбита захоронения • Гиперболическая траектория • Наклонная орбита / Ненаклонная орбита • Оскулирующая орбита • Параболическая траектория • Опорная орбита (в т.ч. низкая) • Синхронная орбита • (Полусинхронная • Субсинхронная) • Стационарная орбита |
| Геоцентрические | Геосинхронная орбита • Геостационарная орбита • Солнечно-синхронная орбита • Низкая околоземная орбита • Средняя околоземная орбита • Высокая околоземная орбита • Молния-орбита • Околоэкваториальная орбита • Орбита Луны • Полярная орбита • Тундра-орбита • TLE |
| Вокруг других небесных тел и точек | Ареосинхронная орбита • Ареостационарная орбита • Гало-орбита • Орбита Лиссажу • Окололунная орбита • Гелиоцентрическая орбита • Солнечно-синхронная орбита |
| Классические |  Наклонение · Наклонение ·  Долгота восходящего узла · Долгота восходящего узла ·  Эксцентриситет · Эксцентриситет ·  Аргумент перицентра · Аргумент перицентра ·  Большая полуось · Большая полуось ·  Средняя аномалия на эпоху Средняя аномалия на эпоху |
| Другие |  Истинная аномалия · Истинная аномалия ·  Малая полуось · Малая полуось ·  Эксцентрическая аномалия · Эксцентрическая аномалия ·  Средняя долгота · Средняя долгота ·  Истинная долгота · Истинная долгота ·  Период обращения Период обращения |
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Орбитальная скорость» в других словарях:
орбитальная скорость — orbitinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Greitis, kuriuo kūnas arba dalelė juda tam tikra orbita. atitikmenys: angl. orbital velocity vok. orbitale Geschwindigkeit, f rus. орбитальная скорость, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
орбитальная скорость — orbitinis greitis statusas T sritis fizika atitikmenys: angl. orbital velocity vok. orbitale Geschwindigkeit, f rus. орбитальная скорость, f pranc. vitesse orbitale, f … Fizikos terminų žodynas
Орбитальная позиция — Запрос «Точка стояния» перенаправляется сюда; см. также другие значения. Точка стояния или Орбитальная позиция положение спутника, находящегося на геостационарной орбите. Поскольку спутник, находящийся на … Википедия
Первая космическая скорость — Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D на эллиптическую. Снаряд E улетает в открытый космос. Первая космическая скорость (кругова … Википедия
Вторая космическая скорость — Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D на эллиптическую. Снаряд E улетает в открытый космос. Вторая космическая скорость (параболическая скорость … Википедия
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Третья космическая скорость — Третья космическая скорость минимальная скорость, которую необходимо сообщить находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы[1][2]. При… … Википедия
Четвёртая космическая скорость — Млечный путь Четвёртая космическая скорость минимально необходимая скорость тела, позволяющая преодолеть притяжение … Википедия
Геостационарная орбита — (ГСО) круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе… … Википедия
Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения. Содержание 1 Эллипс 2 Парабола 3 Гипербола … Википедия
Источник


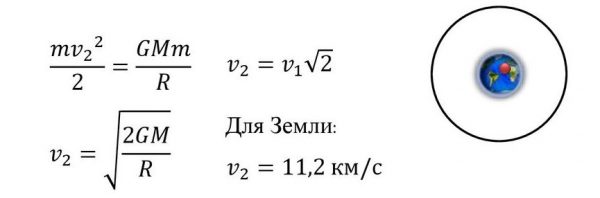




 — гравитационный параметр, равный G(M+m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела
— гравитационный параметр, равный G(M+m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела — фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение
— фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение  — для эллипса и гиперболы)
— для эллипса и гиперболы) — эксцентриситет (
— эксцентриситет (  для эллипса,
для эллипса,  для параболы,
для параболы,  — для гиперболы)
— для гиперболы) — истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела
— истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела



 — расстояние между вращающимся телом и центральным телом
— расстояние между вращающимся телом и центральным телом —удельная орбитальная энергия
—удельная орбитальная энергия соответствуют движению по эллиптическим траекториям
соответствуют движению по эллиптическим траекториям  соответствует движению по параболической траектории и называется так же второй космической скоростью
соответствует движению по параболической траектории и называется так же второй космической скоростью \sqrt<\mu\left(<2\over
\sqrt<\mu\left(<2\over

